Considere el siguiente algoritmo para construir un Montón de una array de entrada A.
CONSTRUIR-MONTÓN (A)
heapsize := tamaño(A);
for i := floor(heapsize/2) downto 1
hacer HEAPIFY(A, i);
fin para
FINAL
Una mirada rápida al algoritmo anterior sugiere que el tiempo de ejecución es ![]() desde que cada llamada a Heapify cuesta
desde que cada llamada a Heapify cuesta ![]() y Build-Heap realiza
y Build-Heap realiza ![]() dichas llamadas.
dichas llamadas.
Este límite superior, aunque correcto, no es asintóticamente estrecho.
Podemos derivar un límite más estrecho al observar que el tiempo de ejecución de Heapify depende de la altura del árbol ‘h’ (que es igual a lg(n), donde n es un número de Nodes) y las alturas de la mayoría de los subárboles son pequeños. La altura ‘h’ aumenta a medida que avanzamos hacia arriba a lo largo del árbol. La línea 3 de Build-Heap ejecuta un bucle desde el índice del último Node interno (heapsize/2) con altura = 1, hasta el índice de raíz (1) con altura = lg (n). Por lo tanto, Heapify toma un tiempo diferente para cada Node, que es:
Para encontrar la Complejidad de tiempo de construir un montón, debemos conocer la cantidad de Nodes que tienen una altura h. Para esto usamos el hecho de que, Un montón de tamaño n tiene como máximo ![]() Nodes con altura h.
Nodes con altura h.
a para derivar la complejidad del tiempo, expresamos el costo total de Build-Heap as-
![]()
El paso 2 usa las propiedades de la notación Big-Oh para ignorar la función techo y la constante 2( ![]() ). De manera similar, en el Paso tres, el límite superior de la suma se puede aumentar hasta el infinito ya que estamos usando la notación Big-Oh. Suma de infinitos GP (x < 1)
). De manera similar, en el Paso tres, el límite superior de la suma se puede aumentar hasta el infinito ya que estamos usando la notación Big-Oh. Suma de infinitos GP (x < 1)
![]()
Derivando ambos lados y multiplicando por x, obtenemos
![]()
Reemplazando el resultado obtenido en (3) en nuestra derivación (1), obtenemos
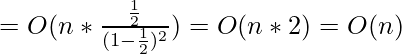
Por lo tanto, se demostró que la complejidad del tiempo para construir un montón binario es ![]() .
.
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA