Comprobar si dos árboles son espejo

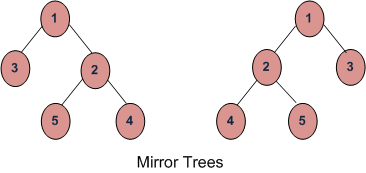
Dados dos árboles binarios, escriba una función que devuelva verdadero si dos árboles son espejo entre sí, de lo contrario, falso. Por ejemplo, la función debería devolver verdadero para los siguientes árboles de entrada.
 

Este problema es diferente del problema discutido aquí .
Para que dos árboles ‘a’ y ‘b’ sean imágenes especulares, deben cumplirse las siguientes tres condiciones: 

1. La clave de su Node raíz debe ser la misma
2. El subárbol izquierdo de la raíz de ‘a’ y el subárbol derecho de la raíz de ‘b’ son espejo.
3. El subárbol derecho de ‘a’ y el subárbol izquierdo de ‘b’ son espejo.

A continuación se muestra la implementación de la idea anterior. 

// C++ program to check if two trees are mirror
// of each other
#include<bits/stdc++.h>
using namespace std;
 
/* A binary tree node has data, pointer to
   left child and a pointer to right child */
struct Node
{
    int data;
    Node* left, *right;
};
 
/* Given two trees, return true if they are
   mirror of each other */
/*As function has to return bool value instead integer value*/
bool areMirror(Node* a, Node* b)
{
    /* Base case : Both empty */
    if (a==NULL && b==NULL)
        return true;
 
    // If only one is empty
    if (a==NULL || b == NULL)
        return false;
 
    /* Both non-empty, compare them recursively
     Note that in recursive calls, we pass left
     of one tree and right of other tree */
    return  a->data == b->data &&
            areMirror(a->left, b->right) &&
            areMirror(a->right, b->left);
}
 
/* Helper function that allocates a new node */
Node* newNode(int data)
{
    Node* node = new Node;
    node->data  = data;
    node->left  =  node->right  = NULL;
    return(node);
}
 
/* Driver program to test areMirror() */
int main()
{
    Node *a = newNode(1);
    Node *b = newNode(1);
    a->left = newNode(2);
    a->right = newNode(3);
    a->left->left  = newNode(4);
    a->left->right = newNode(5);
 
    b->left = newNode(3);
    b->right = newNode(2);
    b->right->left = newNode(5);
    b->right->right = newNode(4);
 
    areMirror(a, b)? cout << "Yes" : cout << "No";
 
    return 0;
}

// Java program to see if two trees
// are mirror of each other
 
// A binary tree node
class Node
{
    int data;
    Node left, right;
 
    public Node(int data)
    {
        this.data = data;
        left = right = null;
    }
}
 
class BinaryTree
{
    Node a, b;
     
    /* Given two trees, return true if they are
       mirror of each other */
    boolean areMirror(Node a, Node b)
    {
        /* Base case : Both empty */
        if (a == null && b == null)
            return true;
 
        // If only one is empty
        if (a == null || b == null)
            return false;
 
        /* Both non-empty, compare them recursively
           Note that in recursive calls, we pass left
           of one tree and right of other tree */
        return a.data == b.data
                && areMirror(a.left, b.right)
                && areMirror(a.right, b.left);
    }
 
    // Driver code to test above methods
    public static void main(String[] args)
    {
        BinaryTree tree = new BinaryTree();
        Node a = new Node(1);
        Node b = new Node(1);
        a.left = new Node(2);
        a.right = new Node(3);
        a.left.left = new Node(4);
        a.left.right = new Node(5);
 
        b.left = new Node(3);
        b.right = new Node(2);
        b.right.left = new Node(5);
        b.right.right = new Node(4);
 
        if (tree.areMirror(a, b) == true)
            System.out.println("Yes");
        else
            System.out.println("No");
 
    }
}
 
// This code has been contributed by Mayank Jaiswal(mayank_24)

# Python3 program to check if two
# trees are mirror of each other
 
# A binary tree node
class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
# Given two trees, return true
# if they are mirror of each other
def areMirror(a, b):
     
    # Base case : Both empty
    if a is None and b is None:
        return True
     
    # If only one is empty
    if a is None or b is None:
        return False
     
    # Both non-empty, compare them
    # recursively. Note that in
    # recursive calls, we pass left
    # of one tree and right of other tree
    return (a.data == b.data and
            areMirror(a.left, b.right) and
            areMirror(a.right , b.left))
 
# Driver code
root1 = Node(1)
root2 = Node(1)
 
root1.left = Node(2)
root1.right = Node(3)
root1.left.left = Node(4)
root1.left.right = Node(5)
 
root2.left = Node(3)
root2.right = Node(2)
root2.right.left = Node(5)
root2.right.right = Node(4)
 
if areMirror(root1, root2):
    print ("Yes")
else:
    print ("No")
 
# This code is contributed by AshishR

using System;
 
// c# program to see if two trees
// are mirror of each other
 
// A binary tree node
public class Node
{
    public int data;
    public Node left, right;
 
    public Node(int data)
    {
        this.data = data;
        left = right = null;
    }
}
 
public class BinaryTree
{
    public Node a, b;
 
    /* Given two trees, return true if they are
    mirror of each other */
    public virtual bool areMirror(Node a, Node b)
    {
        /* Base case : Both empty */
        if (a == null && b == null)
        {
            return true;
        }
 
        // If only one is empty
        if (a == null || b == null)
        {
            return false;
        }
 
        /* Both non-empty, compare them recursively
        Note that in recursive calls, we pass left
        of one tree and right of other tree */
        return a.data == b.data && areMirror(a.left, b.right)
                            && areMirror(a.right, b.left);
    }
 
    // Driver code to test above methods
    public static void Main(string[] args)
    {
        BinaryTree tree = new BinaryTree();
        Node a = new Node(1);
        Node b = new Node(1);
        a.left = new Node(2);
        a.right = new Node(3);
        a.left.left = new Node(4);
        a.left.right = new Node(5);
 
        b.left = new Node(3);
        b.right = new Node(2);
        b.right.left = new Node(5);
        b.right.right = new Node(4);
 
        if (tree.areMirror(a, b) == true)
        {
            Console.WriteLine("Yes");
        }
        else
        {
            Console.WriteLine("No");
        }
 
    }
}
 
// This code is contributed by Shrikant13

<script>
// javascript program to see if two trees
// are mirror of each other
 
// A binary tree node
class Node {
     
     Node(data) {
        this.data = data;
        this.left = this.right = null;
    }
}
 
var a, b;
 
    /*
     * Given two trees, return true if they are mirror of each other
     */
    function areMirror( a,  b) {
        /* Base case : Both empty */
        if (a == null && b == null)
            return true;
 
        // If only one is empty
        if (a == null || b == null)
            return false;
 
        /*
         * Both non-empty, compare them recursively Note that in recursive calls, we
         * pass left of one tree and right of other tree
         */
        return a.data == b.data && areMirror(a.left, b.right) && areMirror(a.right, b.left);
    }
 
    // Driver code to test above methods
     
     
         a = new Node(1);
         b = new Node(1);
        left = new Node(2);
        right = new Node(3);
        left.left = new Node(4);
        left.right = new Node(5);
 
        left = new Node(3);
        right = new Node(2);
        right.left = new Node(5);
        right.right = new Node(4);
 
        if (areMirror(a, b) == true)
            document.write("Yes");
        else
            document.write("No");
 
// This code contributed by umadevi9616
</script>

Yes

Complejidad de tiempo: O(n)
Espacio auxiliar: O(h) donde h es la altura del árbol binario

Método iterativo para verificar si dos árboles son espejo entre sí. 

Este artículo es una contribución de Ashish Gupta . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.