Dada la representación de una lista de adyacencia de un grafo dirigido, la tarea es verificar si el costo de ir de cualquier vértice a cualquier otro vértice a través de todos los caminos posibles es igual o no. Si hay un costo c para ir del vértice A al vértice B , entonces el costo de viajar del vértice B al vértice A será -c .
Ejemplos:
Entrada: array[][] = {{0, 2, 0, 1}, {-2, 0, 1, 0}, {0, -1, 0, -2}, {-1, 0, 2, 0}}
Salida: Sí
Explicación:
Aquí el costo de ir de cualquier Node a cualquier otro Node es igual para todos los caminos posibles. Por ejemplo, si vamos de 1 a 4 vía (1 -> 2 -> 3 -> 4) cuyo costo es (2 + 1 + (-2)) es decir 1 y vía ( 1 -> 4 ) que es a la inversa borde cuyo costo es 1. De manera similar, el costo de todos los demás caminos es igual.
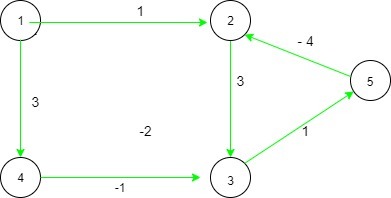
Entrada: array[][] = {{0, 1, 0, 3, 0}, {-1, 0, 3, 0, 4}, {0, -3, 0, 1, 1}, {-3 , 0, -1, 0, 0}, {0, -4, -1, 0, 0}}
Salida: No
Explicación:
Para los siguientes dos caminos desde el borde 1 al 4, (1 -> 2 -> 3 -> 4), Costo = (1 + 3 + 1) = 5 y (1 -> 4), Costo = 3. Dado que los costos son diferencia, la respuesta es no
Enfoque: La idea es mantener dos arrays dis[] que mantiene la distancia de los caminos recorridos y visitó[] que mantiene los vértices visitados. El gráfico se almacena usando un vector 2D de pares. El primer valor del par es el Node de destino y el segundo valor es el costo asociado con él. Ahora, DFS se ejecuta en el gráfico. Las siguientes dos condiciones ocurren para cada vértice:
- Si no se visita el próximo Node a alcanzar, la array dis se actualiza con el valor dis[current_node] + costo del nuevo borde encontrado en el vector 2D, es decir, el Node actual al siguiente Node a alcanzar y se llama a la misma función con el mismo Node no visitado.
- Si se visita el Node, la distancia del próximo Node a alcanzar se compara con el dis[curr] + costo del borde para llegar al siguiente Node. Si son iguales, entonces el indicador de la variable booleana se actualiza con verdadero y el ciclo continúa para los siguientes vértices.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, int> > adj[100005];
// Initialize distance and visited array
int vis[100005] = { 0 },
dist[100005] = { 0 },
flg;
// Function to perform dfs and check
// For a given vertex If the distance
// for all the paths is equal or not
void dfs(int curr)
{
vis[curr] = 1;
for (int i = 0; i < adj[curr].size(); i++) {
// Checking the next node to reach
// is visited or not
if (vis[adj[curr][i].first]) {
// Case 2: comparing the distance
if (dist[adj[curr][i].first]
!= dist[curr] + adj[curr][i].second)
flg = 1;
}
else {
// Case 1: Adding the distance
// and updating the array
dist[adj[curr][i].first] = dist[curr]
+ adj[curr][i].second;
// Calling the function again with the
// same node
dfs(adj[curr][i].first);
}
}
}
// Driver code
int main()
{
int n = 4, m = 4;
flg = 0;
// Creating the graph as mentioned
// in example 1
adj[0].push_back({ 1, 2 });
adj[1].push_back({ 0, -2 });
adj[1].push_back({ 2, 1 });
adj[2].push_back({ 1, -1 });
adj[2].push_back({ 3, -2 });
adj[3].push_back({ 2, 2 });
adj[3].push_back({ 0, -1 });
adj[0].push_back({ 3, 1 });
for (int i = 0; i < n; i++) {
if (flg)
// If for any vertex, flg is true,
// then the distance is not equal
break;
if (!vis[i])
// Calling the DFS function if
// the vertex is not visited
dfs(i);
}
if (flg)
cout << "No" << endl;
else
cout << "Yes" << endl;
return 0;
}
Java
// Java implementation of the above approach
import java.util.*;
class GFG {
static class pair {
int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
static Vector<pair>[] adj = new Vector[100005];
// Initialize distance and visited array
static int[] vis = new int[100005];
static int[] dist = new int[100005];
static int flg;
// Function to perform dfs and check
// For a given vertex If the distance
// for all the paths is equal or not
static void dfs(int curr) {
vis[curr] = 1;
for (int i = 0; i < adj[curr].size(); i++) {
// Checking the next node to reach
// is visited or not
if (vis[adj[curr].get(i).first] > 0) {
// Case 2: comparing the distance
if (dist[adj[curr].get(i).first] !=
dist[curr] + adj[curr].get(i).second)
flg = 1;
} else {
// Case 1: Adding the distance
// and updating the array
dist[adj[curr].get(i).first] =
dist[curr] + adj[curr].get(i).second;
// Calling the function again with the
// same node
dfs(adj[curr].get(i).first);
}
}
}
// Driver code
public static void main(String[] args) {
int n = 4, m = 4;
flg = 0;
for (int i = 0; i < adj.length; i++) {
adj[i] = new Vector<pair>();
}
// Creating the graph as mentioned
// in example 1
adj[0].add(new pair(1, 2));
adj[1].add(new pair(0, -2));
adj[1].add(new pair(2, 1));
adj[2].add(new pair(1, -1));
adj[2].add(new pair(3, -2));
adj[3].add(new pair(2, 2));
adj[3].add(new pair(0, -1));
adj[0].add(new pair(3, 1));
for (int i = 0; i < n; i++) {
if (flg == 1)
// If for any vertex, flg is true,
// then the distance is not equal
break;
if (vis[i] != 1)
// Calling the DFS function if
// the vertex is not visited
dfs(i);
}
if (flg == 1)
System.out.print("No" + "\n");
else
System.out.print("Yes" + "\n");
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 implementation of the above approach
adj = [[] for i in range(100005)]
# Initialize distance and visited array
vis = [0]*100005
dist = [0]*100005
flg = 0
# Function to perform dfs and check
# For a given vertex If the distance
# for all the paths is equal or not
def dfs(curr):
vis[curr] = 1
for i in range(len(adj[curr])):
# Checking the next node to reach
# is visited or not
if (vis[adj[curr][i][0]]):
# Case 2: comparing the distance
if (dist[adj[curr][i][0]]
!= dist[curr] + adj[curr][i][1]):
flg = 1
else:
# Case 1: Adding the distance
# and updating the array
dist[adj[curr][i][0]] = dist[curr]+ adj[curr][i][1]
# Calling the function again with the
# same node
dfs(adj[curr][i][0])
# Driver code
n = 4
m = 4
flg = 0
# Creating the graph as mentioned
# in example 1
adj[0].append([1, 2])
adj[1].append([0, -2])
adj[1].append([2, 1])
adj[2].append([1, -1])
adj[2].append([3, -2])
adj[3].append([2, 2])
adj[3].append([0, -1])
adj[0].append([3, 1])
for i in range(n):
if (flg):
# If for any vertex, flg is true,
# then the distance is not equal
break
if (vis[i] == 0):
# Calling the DFS function if
# the vertex is not visited
dfs(i)
if (flg):
print("No")
else:
print("Yes")
# This code is contributed by mohit kumar 29
C#
// C# implementation of the above approach
using System;
using System.Collections.Generic;
class GFG {
class pair {
public int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
static List<pair>[] adj = new List<pair>[100005];
// Initialize distance and visited array
static int[] vis = new int[100005];
static int[] dist = new int[100005];
static int flg;
// Function to perform dfs and check
// For a given vertex If the distance
// for all the paths is equal or not
static void dfs(int curr) {
vis[curr] = 1;
for (int i = 0; i < adj[curr].Count; i++) {
// Checking the next node to reach
// is visited or not
if (vis[adj[curr][i].first] > 0) {
// Case 2: comparing the distance
if (dist[adj[curr][i].first] !=
dist[curr] + adj[curr][i].second)
flg = 1;
} else {
// Case 1: Adding the distance
// and updating the array
dist[adj[curr][i].first] =
dist[curr] + adj[curr][i].second;
// Calling the function again with the
// same node
dfs(adj[curr][i].first);
}
}
}
// Driver code
public static void Main(String[] args) {
int n = 4;
flg = 0;
for (int i = 0; i < adj.Length; i++) {
adj[i] = new List<pair>();
}
// Creating the graph as mentioned
// in example 1
adj[0].Add(new pair(1, 2));
adj[1].Add(new pair(0, -2));
adj[1].Add(new pair(2, 1));
adj[2].Add(new pair(1, -1));
adj[2].Add(new pair(3, -2));
adj[3].Add(new pair(2, 2));
adj[3].Add(new pair(0, -1));
adj[0].Add(new pair(3, 1));
for (int i = 0; i < n; i++) {
if (flg == 1)
// If for any vertex, flg is true,
// then the distance is not equal
break;
if (vis[i] != 1)
// Calling the DFS function if
// the vertex is not visited
dfs(i);
}
if (flg == 1)
Console.Write("No" + "\n");
else
Console.Write("Yes" + "\n");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript implementation of the above approach
let adj = new Array(100005);
// Initialize distance and visited array
let vis = new Array(100005);
let dist = new Array(100005);
for(let i = 0; i < 100005; i++)
{
vis[i] = 0;
dist[i] = 0;
}
let flg;
// Function to perform dfs and check
// For a given vertex If the distance
// for all the paths is equal or not
function dfs(curr)
{
vis[curr] = 1;
for(let i = 0; i < adj[curr].length; i++)
{
// Checking the next node to reach
// is visited or not
if (vis[adj[curr][i][0]] > 0)
{
// Case 2: comparing the distance
if (dist[adj[curr][i][0]] !=
dist[curr] + adj[curr][i][1])
flg = 1;
}
else
{
// Case 1: Adding the distance
// and updating the array
dist[adj[curr][i][0]] = dist[curr] +
adj[curr][i][1];
// Calling the function again with the
// same node
dfs(adj[curr][i][0]);
}
}
}
// Driver code
let n = 4, m = 4;
flg = 0;
for(let i = 0; i < adj.length; i++)
{
adj[i] = [];
}
// Creating the graph as mentioned
// in example 1
adj[0].push([1, 2]);
adj[1].push([0, -2]);
adj[1].push([2, 1]);
adj[2].push([1, -1]);
adj[2].push([3, -2]);
adj[3].push([2, 2]);
adj[3].push([0, -1]);
adj[0].push([3, 1]);
for(let i = 0; i < n; i++)
{
if (flg == 1)
// If for any vertex, flg is true,
// then the distance is not equal
break;
if (vis[i] != 1)
// Calling the DFS function if
// the vertex is not visited
dfs(i);
}
if (flg == 1)
document.write("No" + "<br>");
else
document.write("Yes" + "<br>");
// This code is contributed by patel2127
</script>
Yes
Complejidad temporal: O(V + E) donde V no es de vértices y E no es de aristas
Publicación traducida automáticamente
Artículo escrito por sharadgoyal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA