Compruebe si el idioma es libre de contexto o no

Requisito previo: lema de bombeo , cómo identificar si un idioma es regular o no
Por lo general, nos enfrentamos a preguntas para identificar cuáles de los idiomas dados están libres de contexto. En el caso de los lenguajes regulares, es comparativamente fácil responder esto, pero para los lenguajes libres de contexto, a veces es complicado. Pumping Lemma nos brinda la capacidad de realizar una prueba negativa, es decir, si un idioma no satisface el lema de bombeo, definitivamente podemos decir que no está libre de contexto, pero si lo satisface, entonces el idioma puede o no estar libre de contexto. Pumping Lemma es más una prueba matemática, lleva más tiempo y aplicarlo en lenguajes libres de contexto es una tarea tediosa y encontrar un contraejemplo para expresiones lingüísticas complejas no es muy fácil. Podemos abordar este problema muy rápidamente, basándonos en observaciones y análisis comunes:

Cada lenguaje regular es libre de contexto.
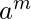
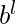
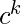
Ejemplo – { 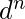$a^m$ $b^l$ $c^k$ $d^n$ | m, l, k, n >= 1 } no tiene contexto, ya que también es regular.
Dada una expresión tal que es posible obtener un centro o punto medio en las strings, podemos realizar una comparación de las subpartes izquierda y derecha usando stack.
Ejemplo 1 – L = {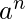 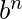$a^n$ $b^n$ | n >= 1} es independiente del contexto, ya que podemos presionar a y luego podemos sacar a para cada ocurrencia de b.
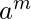
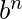
Ejemplo 2: L = { 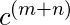$a^m$ $b^n$ $c^{(m+n)}$ } no tiene contexto. Podemos reescribirlo como {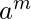 $a^m$ $b^n$ $c^n$ $c^m$ }.

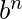
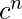
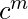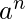
Ejemplo 3: L = { 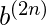$a^n$ $b^{(2n)}$ } no tiene contexto, ya que podemos presionar dos a y sacar una a para cada aparición de b. Por lo tanto, tenemos un punto medio aquí también.

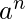
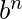
Ejemplo 4: L = { 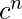$a^n$ $b^n$ $c^n$ } no está libre de contexto.
La expresión dada es una combinación de múltiples expresiones con puntos medios en ellas, de modo que cada subexpresión es independiente de otras subexpresiones, entonces es independiente del contexto.
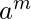
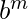
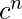
Ejemplo 1: L = { 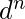$a^m$ $b^m$ $c^n$ $d^n$ } no tiene contexto. Contiene múltiples expresiones con un punto medio en cada una de ellas.
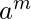
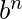
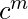
Ejemplo 2: L = { 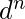$a^m$ $b^n$ $c^m$ $d^n$ } no está libre de contexto.
La expresión dada consiste en una operación en la que se puede encontrar el punto medio junto con algunas expresiones regulares independientes en el medio, lo que da como resultado un lenguaje libre de contexto.
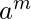
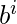
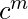
Ejemplo: L = { 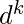$a^m$ $b^i$ $c^m$ $d^k$ } es un lenguaje libre de contexto.
Aquí, tenemos b^i y d^k como expresiones regulares independientes en el medio, lo que no afecta la pila.
Una expresión que no forma un patrón en el que se pueda realizar una comparación lineal usando stack no es un lenguaje libre de contexto.
Ejemplo 1: L = { a^mb^n^2 } no está libre de contexto.
Ejemplo 2: L = { a^nb^2^n } no está libre de contexto.
Ejemplo 3: L = { a^n^2 } no está libre de contexto.
Ejemplo 4 – L = {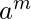 $a^m$ | m es primo } no está libre de contexto.
Una expresión que implica el conteo y la comparación de tres o más variables de forma independiente no es un lenguaje libre de contexto, ya que la pila permite la comparación de solo dos variables a la vez.
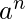
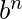
Ejemplo 1: L = { 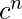$a^n$ $b^n$ $c^n$ } no está libre de contexto.
Ejemplo 2 – L = { w | na(w) = nb(w) = nc(w) } no está libre de contexto.

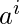
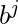
Ejemplo 3 – L = { 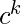$a^i$ $b^j$ $c^k$ | i > j > k } no está libre de contexto.
Un punto para recordar es contar y la comparación solo se puede hacer con la parte superior de la pila y no con la parte inferior de la pila en Push Down Automata, por lo tanto, un lenguaje que exhibe una característica que implica la comparación con la parte inferior de la pila no es un lenguaje libre de contexto.
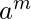
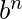
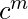
Ejemplo 1: L = { 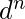$a^m$ $b^n$ $c^m$ $d^n$ } no está libre de contexto.
Empujando a’s primero y luego b’s. Ahora, no podremos comparar c con a ya que la parte superior de la pila tiene b.
Ejemplo 2 – L = {WW | W pertenece a {a, b}* } no está libre de contexto.
Uno podría pensar en dibujar un autómata de empuje hacia abajo no determinista, pero no ayudará ya que el primer símbolo estará en la parte inferior de la pila y cuando comience la segunda W, no podremos compararlo con la parte inferior de la pila.
Si podemos encontrar el punto medio en la expresión incluso de una manera no determinista, entonces es un lenguaje libre de contexto.
Ejemplo 1 – L = { W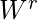 $W^r$ | W pertenece a {a, b}* } es un lenguaje libre de contexto.
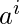
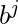
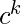
Ejemplo 2 – L = { 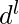$a^i$ $b^j$ $c^k$ $d^l$ | i=k o j=l } es un lenguaje libre de contexto.

Publicación traducida automáticamente

Artículo escrito por antOnTheWall y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta