Compruebe si Matrix T es el resultado de una o más rotaciones de 90° de Matrix mat

Dadas dos arrays 2D mat[][] y T[][] de tamaño M×N y P×Q respectivamente. La tarea es comprobar si la array T[][] es el resultado de una o más rotaciones de 90° de la array mat[][] .

Ejemplos:

Entrada: mat[][] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, T[][] ={{7, 4, 1}, { 8, 5, 2}, {9, 6, 3}}
Salida: Sí
Explicación:

De las cifras dadas arriba, está claro que T[][] se obtiene girando 90° una vez.

Entrada: mat[][] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, T[][] = {{1, 4, 7}, { 8, 5, 2}, {9, 6, 3}}
Salida: No

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones: 

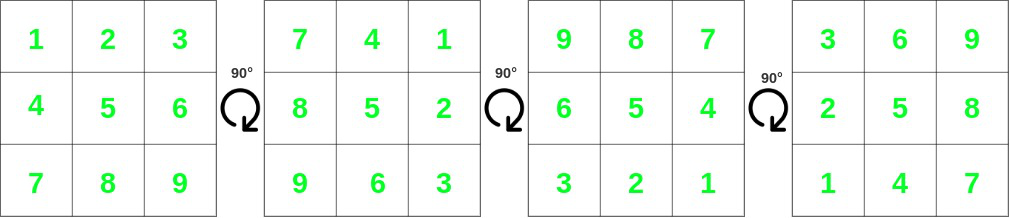
• Considere la siguiente array 2D:

• Al rotarlo varias veces 90° se obtienen las siguientes arrays:

• De las figuras anteriores, se puede ver que cada fila puede ocurrir tal cual o en su forma invertida .

• Lo mismo se puede observar para las columnas

Por lo tanto, si T[][] es una de las formas rotadas de mat[][] , debe tener al menos una ocurrencia de la forma original o invertida de las filas y columnas de mat[][] presentes como sus filas y columnas 

Siga los pasos a continuación para resolver el problema:

• Si las dimensiones de mat[][] y T[][] no son iguales o no, imprima “ No ” y regrese.
• Inicialice un mapa de vectores , digamos m para almacenar las frecuencias de todas las filas, columnas y sus versiones invertidas.
• Iterar en el rango [0, M-1] y usando la variable i y realizar los siguientes pasos:
  • Incremente m[mat[i]] en 1 y luego invierta el vector mat[i] y luego incremente m[mat[i]] en 1 .
• Iterar en el rango [0, N-1] y usando la variable i y realizar los siguientes pasos:
  • Empuje todos los elementos de la i ^-ésima columna en un vector digamos r.
  • Incremente m[r] en 1 y luego invierta el vector r y luego incremente m[r] en 1.
• Iterar en el rango [0, M-1] y usando la variable i y realizar los siguientes pasos:
  • Si m[T[i]] es menor que 0 , imprima “ No ” y regrese.
  • De lo contrario, disminuya m[T[i]] en 1 .
• Iterar en el rango [0, N-1] y usando la variable i y realizar los siguientes pasos:
  • Empuje todos los elementos de la i ^-ésima columna de T[][] en un vector digamos r.
  • Si m[r] es menor que 0, imprima “ No ” y regrese.
  • De lo contrario, disminuya m[r] en 1 .
• Finalmente, si ninguno de los casos anteriores satisface, imprima » Sí «.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to check whether another
// matrix can be created by rotating
// mat one or more times by 90 degrees
string findRotation(vector<vector<int> >& mat,
                    vector<vector<int> >& T)
{
    // If the dimensions of both the
    // arrays don't match
    if (T.size() != mat.size()
        || T[0].size() != mat[0].size()) {
        // Return false
        return "No";
    }
 
    // Map to store all rows, columns
    // and their reversed versions
    map<vector<int>, int> m;
 
    // Iterate in the range [0, M-1]
    for (int i = 0; i < mat.size(); i++) {
 
        // Increment the frequency of the
        // i'th row by 1
        m[mat[i]] += 1;
 
        // Reverse the i'th row
        reverse(mat[i].begin(), mat[i].end());
 
        // Increment the frequency of the
        // i'th row by 1
        m[mat[i]] += 1;
    }
 
    // Iterate in the range [0, N-1]
    for (int i = 0; i < mat[0].size(); i++) {
 
        // Stores the i'th column
        vector<int> r = {};
 
        // Iterate in the range [0, M-1]
        for (int j = 0; j < mat.size(); j++) {
            r.push_back(mat[j][i]);
        }
 
        // Increment the frequency of the
        // i'th column by 1
        m[r] += 1;
 
        // Reverse the i'th column
        reverse(r.begin(), r.end());
 
        // Increment the frequency of the
        // i'th column by 1
        m[r] += 1;
    }
 
    // Iterate in the range [0, M-1]
    for (int i = 0; i < T.size(); i++) {
 
        // If frequency of the i'th row
        // is more in T[][] than in the
        // mat[][].
        if (m[T[i]] <= 0) {
            return "No";
        }
 
        // Decrement the frequency of the
        // i'th row by 1
        m[T[i]] -= 1;
    }
 
    // Iterate in the range [0, N-1]
    for (int i = 0; i < T[0].size(); i++) {
 
        // Stores the ith column
        vector<int> r = {};
 
        // Iterate in the range [0, M-1]
        for (int j = 0; j < T.size(); j++) {
            r.push_back(T[j][i]);
        }
 
        // If frequency of the i'th column
        // is more in T[][] than in mat[][].
        if (m[r] <= 0) {
            return "No";
        }
 
        // Decrement the frequency of the i'th
        // column by 1
        m[r] -= 1;
    }
 
    // Return "Yes"
    return "Yes";
}
 
// Driver code
int main()
{
    // Input
    vector<vector<int> > mat
        = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
    vector<vector<int> > T
        = { { 3, 6, 9 }, { 2, 5, 8 }, { 1, 4, 7 } };
 
    // Function call
    cout << findRotation(mat, T);
 
    return 0;
}

<script>
 
// JavaScript program for the above approach
 
 
// Function to check whether another
// matrix can be created by rotating
// mat one or more times by 90 degrees
function findRotation(mat, T)
{
    // If the dimensions of both the
    // arrays don't match
    if (T.length != mat.length
        || T[0].length != mat[0].length) {
        // Return false
        return "No";
    }
 
    // Map to store all rows, columns
    // and their reversed versions
    let m = new Map();
 
    // Iterate in the range [0, M-1]
    for (let i = 0; i < mat.length; i++) {
 
        // Increment the frequency of the
        // i'th row by 1
        if(m.has(mat[i])){
            m.set(mat[i], m.get(mat[i]) + 1)
        }else{
            m.set(mat[i], 1)
        }
 
        // Reverse the i'th row
        mat[i].reverse();
 
        // Increment the frequency of the
        // i'th row by 1
        if(m.has(mat[i])){
            m.set(mat[i], m.get(mat[i]) + 1)
        }else{
            m.set(mat[i], 1)
        }
    }
 
    // Iterate in the range [0, N-1]
    for (let i = 0; i < mat[0].length; i++) {
 
        // Stores the i'th column
        let r = [];
 
        // Iterate in the range [0, M-1]
        for (let j = 0; j < mat.length; j++) {
            r.push(mat[j][i]);
        }
 
        // Increment the frequency of the
        // i'th column by 1
 
        if(m.has(r)){
            m.set(r, m.get(r) + 1)
        }else{
            m.set(r, 1)
        }
 
        // Reverse the i'th column
        r.reverse();
 
        // Increment the frequency of the
        // i'th column by 1
        if(m.has(r)){
            m.set(r, m.get(r) + 1)
        }else{
            m.set(r, 1)
        }
    }
 
    // Iterate in the range [0, M-1]
    for (let i = 0; i < T.length; i++) {
 
        // If frequency of the i'th row
        // is more in T[][] than in the
        // mat[][].
        if (m.get(T[i]) <= 0) {
            return "No";
        }
 
        // Decrement the frequency of the
        // i'th row by 1
        m.set(T[i], m.get(T[i]) - 1);
    }
 
    // Iterate in the range [0, N-1]
    for (let i = 0; i < T[0].length; i++) {
 
        // Stores the ith column
        let r = [];
 
        // Iterate in the range [0, M-1]
        for (let j = 0; j < T.length; j++) {
            r.push(T[j][i]);
        }
 
        // If frequency of the i'th column
        // is more in T[][] than in mat[][].
        if (m.get(r) <= 0) {
            return "No";
        }
 
        // Decrement the frequency of the i'th
        // column by 1
        m.set(r, m.get(r) - 1);
    }
 
    // Return "Yes"
    return "Yes";
}
 
// Driver code
 
    // Input
    let mat
        = [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ];
    let T
        = [ [ 3, 6, 9 ], [ 2, 5, 8 ], [ 1, 4, 7 ] ];
 
    // Function call
    document.write(findRotation(mat, T));
     
</script>

Yes

Complejidad Temporal: O(N*M)
Espacio Auxiliar: (N*M)