Dados dos árboles binarios, tenemos que comprobar si cada uno de sus niveles son anagramas entre sí o no.
Ejemplo:
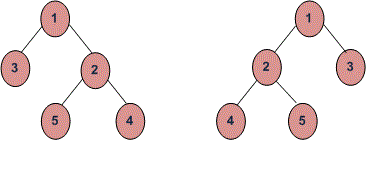
C++
/* Iterative program to check if two trees are level
by level anagram. */
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node
{
struct Node *left, *right;
int data;
};
// Returns true if trees with root1 and root2
// are level by level anagram, else returns false.
bool areAnagrams(Node *root1, Node *root2)
{
// Base Cases
if (root1 == NULL && root2 == NULL)
return true;
if (root1 == NULL || root2 == NULL)
return false;
// start level order traversal of two trees
// using two queues.
queue<Node *> q1, q2;
q1.push(root1);
q2.push(root2);
while (1)
{
// n1 (queue size) indicates number of Nodes
// at current level in first tree and n2 indicates
// number of nodes in current level of second tree.
int n1 = q1.size(), n2 = q2.size();
// If n1 and n2 are different
if (n1 != n2)
return false;
// If level order traversal is over
if (n1 == 0)
break;
// Dequeue all Nodes of current level and
// Enqueue all Nodes of next level
vector<int> curr_level1, curr_level2;
while (n1 > 0)
{
Node *node1 = q1.front();
q1.pop();
if (node1->left != NULL)
q1.push(node1->left);
if (node1->right != NULL)
q1.push(node1->right);
n1--;
Node *node2 = q2.front();
q2.pop();
if (node2->left != NULL)
q2.push(node2->left);
if (node2->right != NULL)
q2.push(node2->right);
curr_level1.push_back(node1->data);
curr_level2.push_back(node2->data);
}
// Check if nodes of current levels are
// anagrams or not.
sort(curr_level1.begin(), curr_level1.end());
sort(curr_level2.begin(), curr_level2.end());
if (curr_level1 != curr_level2)
return false;
}
return true;
}
// Utility function to create a new tree Node
Node* newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Constructing both the trees.
struct Node* root1 = newNode(1);
root1->left = newNode(3);
root1->right = newNode(2);
root1->right->left = newNode(5);
root1->right->right = newNode(4);
struct Node* root2 = newNode(1);
root2->left = newNode(2);
root2->right = newNode(3);
root2->left->left = newNode(4);
root2->left->right = newNode(5);
areAnagrams(root1, root2)? cout << "Yes" : cout << "No";
return 0;
}
Java
/* Iterative program to check if two trees
are level by level anagram. */
import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;
public class GFG
{
// A Binary Tree Node
static class Node
{
Node left, right;
int data;
Node(int data){
this.data = data;
left = null;
right = null;
}
}
// Returns true if trees with root1 and root2
// are level by level anagram, else returns false.
static boolean areAnagrams(Node root1, Node root2)
{
// Base Cases
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
// start level order traversal of two trees
// using two queues.
Queue<Node> q1 = new LinkedList<Node>();
Queue<Node> q2 = new LinkedList<Node>();
q1.add(root1);
q2.add(root2);
while (true)
{
// n1 (queue size) indicates number of
// Nodes at current level in first tree
// and n2 indicates number of nodes in
// current level of second tree.
int n1 = q1.size(), n2 = q2.size();
// If n1 and n2 are different
if (n1 != n2)
return false;
// If level order traversal is over
if (n1 == 0)
break;
// Dequeue all Nodes of current level and
// Enqueue all Nodes of next level
ArrayList<Integer> curr_level1 = new
ArrayList<>();
ArrayList<Integer> curr_level2 = new
ArrayList<>();
while (n1 > 0)
{
Node node1 = q1.peek();
q1.remove();
if (node1.left != null)
q1.add(node1.left);
if (node1.right != null)
q1.add(node1.right);
n1--;
Node node2 = q2.peek();
q2.remove();
if (node2.left != null)
q2.add(node2.left);
if (node2.right != null)
q2.add(node2.right);
curr_level1.add(node1.data);
curr_level2.add(node2.data);
}
// Check if nodes of current levels are
// anagrams or not.
Collections.sort(curr_level1);
Collections.sort(curr_level2);
if (!curr_level1.equals(curr_level2))
return false;
}
return true;
}
// Driver program to test above functions
public static void main(String args[])
{
// Constructing both the trees.
Node root1 = new Node(1);
root1.left = new Node(3);
root1.right = new Node(2);
root1.right.left = new Node(5);
root1.right.right = new Node(4);
Node root2 = new Node(1);
root2.left = new Node(2);
root2.right = new Node(3);
root2.left.left = new Node(4);
root2.left.right = new Node(5);
System.out.println(areAnagrams(root1, root2)?
"Yes" : "No");
}
}
// This code is contributed by Sumit Ghosh
Python3
# Iterative program to check if two
# trees are level by level anagram
# A Binary Tree Node
# Utility function to create a
# new tree Node
class newNode:
def __init__(self, data):
self.data = data
self.left = self.right = None
# Returns true if trees with root1
# and root2 are level by level
# anagram, else returns false.
def areAnagrams(root1, root2) :
# Base Cases
if (root1 == None and root2 == None) :
return True
if (root1 == None or root2 == None) :
return False
# start level order traversal of
# two trees using two queues.
q1 = []
q2 = []
q1.append(root1)
q2.append(root2)
while (1) :
# n1 (queue size) indicates number
# of Nodes at current level in first
# tree and n2 indicates number of nodes
# in current level of second tree.
n1 = len(q1)
n2 = len(q2)
# If n1 and n2 are different
if (n1 != n2):
return False
# If level order traversal is over
if (n1 == 0):
break
# Dequeue all Nodes of current level
# and Enqueue all Nodes of next level
curr_level1 = []
curr_level2 = []
while (n1 > 0):
node1 = q1[0]
q1.pop(0)
if (node1.left != None) :
q1.append(node1.left)
if (node1.right != None) :
q1.append(node1.right)
n1 -= 1
node2 = q2[0]
q2.pop(0)
if (node2.left != None) :
q2.append(node2.left)
if (node2.right != None) :
q2.append(node2.right)
curr_level1.append(node1.data)
curr_level2.append(node2.data)
# Check if nodes of current levels
# are anagrams or not.
curr_level1.sort()
curr_level2.sort()
if (curr_level1 != curr_level2) :
return False
return True
# Driver Code
if __name__ == '__main__':
# Constructing both the trees.
root1 = newNode(1)
root1.left = newNode(3)
root1.right = newNode(2)
root1.right.left = newNode(5)
root1.right.right = newNode(4)
root2 = newNode(1)
root2.left = newNode(2)
root2.right = newNode(3)
root2.left.left = newNode(4)
root2.left.right = newNode(5)
if areAnagrams(root1, root2):
print("Yes")
else:
print("No")
# This code is contributed
# by SHUBHAMSINGH10
C#
/* Iterative program to check if two trees
are level by level anagram. */
using System;
using System.Collections.Generic;
class GFG
{
// A Binary Tree Node
public class Node
{
public Node left, right;
public int data;
public Node(int data)
{
this.data = data;
left = null;
right = null;
}
}
// Returns true if trees with root1
// and root2 are level by level anagram,
// else returns false.
static Boolean areAnagrams(Node root1,
Node root2)
{
// Base Cases
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
// start level order traversal of two trees
// using two queues.
Queue<Node> q1 = new Queue<Node>();
Queue<Node> q2 = new Queue<Node>();
q1.Enqueue(root1);
q2.Enqueue(root2);
while (true)
{
// n1 (queue size) indicates number of
// Nodes at current level in first tree
// and n2 indicates number of nodes in
// current level of second tree.
int n1 = q1.Count, n2 = q2.Count;
// If n1 and n2 are different
if (n1 != n2)
return false;
// If level order traversal is over
if (n1 == 0)
break;
// Dequeue all Nodes of current level and
// Enqueue all Nodes of next level
List<int> curr_level1 = new List<int>();
List<int> curr_level2 = new List<int>();
while (n1 > 0)
{
Node node1 = q1.Peek();
q1.Dequeue();
if (node1.left != null)
q1.Enqueue(node1.left);
if (node1.right != null)
q1.Enqueue(node1.right);
n1--;
Node node2 = q2.Peek();
q2.Dequeue();
if (node2.left != null)
q2.Enqueue(node2.left);
if (node2.right != null)
q2.Enqueue(node2.right);
curr_level1.Add(node1.data);
curr_level2.Add(node2.data);
}
// Check if nodes of current levels are
// anagrams or not.
curr_level1.Sort();
curr_level2.Sort();
for(int i = 0;
i < curr_level1.Count; i++)
if(curr_level1[i] != curr_level2[i])
return false;
}
return true;
}
// Driver Code
public static void Main(String []args)
{
// Constructing both the trees.
Node root1 = new Node(1);
root1.left = new Node(3);
root1.right = new Node(2);
root1.right.left = new Node(5);
root1.right.right = new Node(4);
Node root2 = new Node(1);
root2.left = new Node(2);
root2.right = new Node(3);
root2.left.left = new Node(4);
root2.left.right = new Node(5);
Console.WriteLine(areAnagrams(root1,
root2) ?
"Yes" : "No");
}
}
// This code is contributed by Arnab Kundu
Javascript
<script>
// Iterative program to check if two
// trees are level by level anagram
// A Binary Tree Node
// Utility function to create a
// new tree Node
class newNode{
constructor(data){
this.data = data
this.left = this.right = null
}
}
// Returns true if trees with root1
// and root2 are level by level
// anagram, else returns false.
function areAnagrams(root1, root2){
// Base Cases
if (root1 == null && root2 == null)
return true
if (root1 == null || root2 == null)
return false
// start level order traversal of
// two trees using two queues.
let q1 = []
let q2 = []
q1.push(root1)
q2.push(root2)
while (1){
// n1 (queue size) indicates number
// of Nodes at current level in first
// tree and n2 indicates number of nodes
// in current level of second tree.
let n1 = q1.length
let n2 = q2.length
// If n1 and n2 are different
if (n1 != n2)
return false
// If level order traversal is over
if (n1 == 0)
break
// Dequeue all Nodes of current level
// and Enqueue all Nodes of next level
let curr_level1 = []
let curr_level2 = []
while (n1 > 0){
let node1 = q1.shift()
if (node1.left != null)
q1.push(node1.left)
if (node1.right != null)
q1.push(node1.right)
n1 -= 1
let node2 = q2.shift()
if (node2.left != null)
q2.push(node2.left)
if (node2.right != null)
q2.push(node2.right)
curr_level1.push(node1.data)
curr_level2.push(node2.data)
}
// Check if nodes of current levels
// are anagrams or not.
curr_level1.sort()
curr_level2.sort()
if (curr_level1.join() != curr_level2.join())
return false
}
return true
}
// Driver Code
// Constructing both the trees.
let root1 = new newNode(1)
root1.left = new newNode(3)
root1.right = new newNode(2)
root1.right.left = new newNode(5)
root1.right.right = new newNode(4)
let root2 = new newNode(1)
root2.left = new newNode(2)
root2.right = new newNode(3)
root2.left.left = new newNode(4)
root2.left.right = new newNode(5)
if(areAnagrams(root1, root2))
document.write("Yes","</br>")
else
document.write("No","</br>")
// This code is contributed by shinjanpatra
</script>
C++
/* Iterative program to check if two trees are level
by level anagram. */
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node {
struct Node *left, *right;
int data;
};
// Returns true if trees with root1 and root2
// are level by level anagram, else returns false.
bool areAnagrams(Node* root1, Node* root2)
{
// Base Cases
if (root1 == NULL && root2 == NULL)
return true;
if (root1 == NULL || root2 == NULL)
return false;
// start level order traversal of two trees
// using two queues.
queue<Node*> q1, q2;
q1.push(root1);
q2.push(root2);
// Hashmap to store the elements that occur in each
// level.
unordered_map<int, int> m;
while (!q1.empty() && !q2.empty()) {
// n1 (queue size) indicates number of Nodes
// at current level in first tree and n2 indicates
// number of nodes in current level of second tree.
int n1 = q1.size(), n2 = q2.size();
// If n1 and n2 are different
if (n1 != n2)
return false;
// If level order traversal is over
if (n1 == 0)
break;
// Dequeue all Nodes of current level and
// Enqueue all Nodes of next level
while (n1--) {
Node* node1 = q1.front();
q1.pop();
// Insert element into hashmap
m[node1->data]++;
// Insert left and right nodes into queue if
// exists.
if (node1->left != NULL)
q1.push(node1->left);
if (node1->right != NULL)
q1.push(node1->right);
}
while (n2--) {
Node* node2 = q2.front();
q2.pop();
// if element from second tree isn't present in
// the first tree of same level then it can't be
// an anagram.
if (m.find(node2->data) == m.end())
return false;
// Reduce frequency of element if present else
// adds it element to hash map with negative
// frequency.
m[node2->data]--;
// If frequency of the element becomes zero then
// remove the element from hashmap.
if (m[node2->data] == 0)
m.erase(node2->data);
// Insert left and right nodes into queue if
// exists.
if (node2->left != NULL)
q2.push(node2->left);
if (node2->right != NULL)
q2.push(node2->right);
}
// If nodes of current levels are anagrams the
// hashmap wouldn't contain any elements.
if (m.size() > 0)
return false;
}
if(q1.empty() && q2.empty())
return true;
return false;
}
// Utility function to create a new tree Node
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Constructing both the trees.
struct Node* root1 = newNode(1);
root1->left = newNode(3);
root1->right = newNode(2);
root1->right->left = newNode(5);
root1->right->right = newNode(4);
struct Node* root2 = newNode(1);
root2->left = newNode(2);
root2->right = newNode(3);
root2->left->left = newNode(4);
root2->left->right = newNode(5);
areAnagrams(root1, root2) ? cout << "Yes"
: cout << "No";
return 0;
}
// This code is contributed by Kasina Dheeraj.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA