Comprueba si un gráfico dirigido dado está fuertemente conectado | Conjunto 2 (Kosaraju usando BFS)

Dada una gráfica dirigida, averigüe si la gráfica es fuertemente conexa o no. Un grafo dirigido es fuertemente conexo si hay un camino entre dos pares cualesquiera de vértices. Existen diferentes métodos para verificar la conectividad del gráfico dirigido, pero uno de los métodos optimizados es el algoritmo simple basado en DFS de Kosaraju . 

El algoritmo simple basado en BFS de Kosaraju también funciona con el mismo principio que el algoritmo basado en DFS. 

Following is Kosaraju’s BFS based simple algorithm
that does two BFS traversals of graph:
1) Initialize all vertices as not visited.

2) Do a BFS traversal of graph starting from 
   any arbitrary vertex v. If BFS traversal 
   doesn’t visit all vertices, then return false.

3) Reverse all edges (or find transpose or reverse 
   of graph)

4) Mark all vertices as not visited in reversed graph.

5) Again do a BFS traversal of reversed graph starting
   from same vertex v (Same as step 2). If BFS traversal
   doesn’t visit all vertices, then return false. 
   Otherwise, return true.

La idea es nuevamente simple si cada Node puede ser alcanzado desde un vértice v, y cada Node puede alcanzar el mismo vértice v, entonces el grafo está fuertemente conectado. En el paso 2, verificamos si todos los vértices son accesibles desde v. En el paso 5, verificamos si todos los vértices pueden alcanzar v (en el gráfico invertido, si todos los vértices son accesibles desde v, entonces todos los vértices pueden alcanzar v en el gráfico original).

Explicación con algunos ejemplos: 

Ejemplo 1: 
Dada una dirección para verificar si está fuertemente conectado o no. 

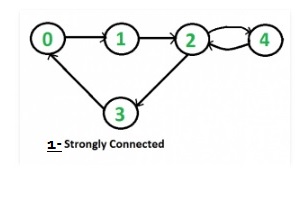
• paso 1: Comenzando con el vértice 2 BFS obtenido es 2 3 4 0 1
• Paso 2: después de invertir el gráfico dado, obtuvimos el gráfico enumerado. 

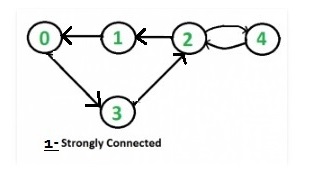
• paso 3: nuevamente después de comenzar con el vértice 2, el BFS es 2 1 4 0 3
• paso 4: Ningún vértice en ambos casos (paso 1 y paso 3) permanece sin visitar.
• paso 5: Entonces, el gráfico dado está fuertemente conectado.

Ejemplo 2: 

Dada una dirección para verificar si está fuertemente conectado o no. 

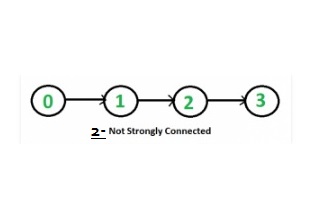
• paso 1: Comenzando con el vértice 2 BFS obtenido es 2 3 4 
• Paso 2: después de invertir el gráfico dado, obtuvimos el gráfico enumerado. 

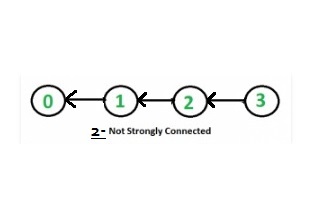
• paso 3: nuevamente después de comenzar con el vértice 2, el BFS es 2 1 0 
• paso 4: el vértice 0, 1 en el gráfico original y 3, 4 en el gráfico inverso permanece sin visitar.
• paso 5: Entonces, el gráfico dado no está fuertemente conectado.

A continuación se muestra la implementación del algoritmo anterior. 

// C++ program to check if a given directed graph
// is strongly connected or not with BFS use
#include <bits/stdc++.h>
using namespace std;
 
class Graph
{
    int V;    // No. of vertices
    list<int> *adj;    // An array of adjacency lists
 
    // A recursive function to print DFS starting from v
    void BFSUtil(int v, bool visited[]);
public:
 
    // Constructor and Destructor
    Graph(int V) { this->V = V;  adj = new list<int>[V];}
    ~Graph() { delete [] adj; }
 
    // Method to add an edge
    void addEdge(int v, int w);
 
    // The main function that returns true if the
    // graph is strongly connected, otherwise false
    bool isSC();
 
    // Function that returns reverse (or transpose)
    // of this graph
    Graph getTranspose();
};
 
// A recursive function to print DFS starting from v
void Graph::BFSUtil(int v, bool visited[])
{
    // Create a queue for BFS
    list<int> queue;
 
    // Mark the current node as visited and enqueue it
    visited[v] = true;
    queue.push_back(v);
 
    // 'i' will be used to get all adjacent vertices
    // of a vertex
    list<int>::iterator i;
 
    while (!queue.empty())
    {
        // Dequeue a vertex from queue
        v = queue.front();
        queue.pop_front();
 
        // Get all adjacent vertices of the dequeued vertex s
        // If a adjacent has not been visited, then mark it
        // visited and enqueue it
        for (i = adj[v].begin(); i != adj[v].end(); ++i)
        {
            if (!visited[*i])
            {
                visited[*i] = true;
                queue.push_back(*i);
            }
        }
    }
}
 
// Function that returns reverse (or transpose) of this graph
Graph Graph::getTranspose()
{
    Graph g(V);
    for (int v = 0; v < V; v++)
    {
        // Recur for all the vertices adjacent to this vertex
        list<int>::iterator i;
        for (i = adj[v].begin(); i != adj[v].end(); ++i)
            g.adj[*i].push_back(v);
    }
    return g;
}
 
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
}
 
// The main function that returns true if graph
// is strongly connected
bool Graph::isSC()
{
    // Step 1: Mark all the vertices as not
    // visited (For first BFS)
    bool visited[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;
 
    // Step 2: Do BFS traversal starting
    // from first vertex.
    BFSUtil(0, visited);
 
    // If BFS traversal doesn’t visit all
    // vertices, then return false.
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
             return false;
 
    // Step 3: Create a reversed graph
    Graph gr = getTranspose();
 
    // Step 4: Mark all the vertices as not
    // visited (For second BFS)
    for(int i = 0; i < V; i++)
        visited[i] = false;
 
    // Step 5: Do BFS for reversed graph
    // starting from first vertex.
    // Starting Vertex must be same starting
    // point of first DFS
    gr.BFSUtil(0, visited);
 
    // If all vertices are not visited in
    // second DFS, then return false
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
             return false;
 
    return true;
}
 
// Driver program to test above functions
int main()
{
    // Create graphs given in the above diagrams
    Graph g1(5);
    g1.addEdge(0, 1);
    g1.addEdge(1, 2);
    g1.addEdge(2, 3);
    g1.addEdge(3, 0);
    g1.addEdge(2, 4);
    g1.addEdge(4, 2);
    g1.isSC()? cout << "Yes\n" : cout << "No\n";
 
    Graph g2(4);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.addEdge(2, 3);
    g2.isSC()? cout << "Yes\n" : cout << "No\n";
 
    return 0;
}

# Python3 program to check if a given directed graph
# is strongly connected or not with BFS use
from collections import deque
 
# A recursive function to print DFS starting from v
def BFSUtil(adj, v, visited):
     
    # Create a queue for BFS
    queue = deque()
 
    # Mark the current node as visited
    # and enqueue it
    visited[v] = True
    queue.append(v)
 
    # 'i' will be used to get all adjacent
    # vertices of a vertex
    while (len(queue) > 0):
         
        # Dequeue a vertex from queue
        v = queue.popleft()
        #print(v)
        #queue.pop_front()
 
        # Get all adjacent vertices of the
        # dequeued vertex s. If a adjacent
        # has not been visited, then mark it
        # visited and enqueue it
        for i in adj[v]:
            if (visited[i] == False):
                visited[i] = True
                queue.append(i)
                 
    return visited
 
# Function that returns reverse
# (or transpose) of this graph
def getTranspose(adj, V):
     
    g = [[] for i in range(V)]
 
    for v in range(V):
         
        # Recur for all the vertices adjacent to
        # this vertex
        # list<int>::iterator i
        for i in adj[v]:
            g[i].append(v)
 
    return g
 
def addEdge(adj, v, w):
     
    # Add w to v’s list.
    adj[v].append(w)
    return adj
 
# The main function that returns True if graph
# is strongly connected
def isSC(adj, V):
     
    # Step 1: Mark all the vertices as not
    # visited (For first BFS)
    visited = [False]*V
 
    # Step 2: Do BFS traversal starting
    # from first vertex.
    visited = BFSUtil(adj, 0, visited)
    # print(visited)
 
    # If BFS traversal doesn’t visit all
    # vertices, then return false.
    for i in range(V):
        if (visited[i] == False):
             return False
 
    # Step 3: Create a reversed graph
    adj = getTranspose(adj, V)
 
    # Step 4: Mark all the vertices as not
    # visited (For second BFS)
    for i in range(V):
        visited[i] = False
 
    # Step 5: Do BFS for reversed graph
    # starting from first vertex.
    # Starting Vertex must be same starting
    # point of first DFS
    visited = BFSUtil(adj, 0, visited)
 
    # If all vertices are not visited in
    # second DFS, then return false
    for i in range(V):
        if (visited[i] == False):
             return False
 
    return True
 
# Driver code
if __name__ == '__main__':
     
    # Create graphs given in the above diagrams
    g1 = [[] for i in range(5)]
    g1 = addEdge(g1, 0, 1)
    g1 = addEdge(g1, 1, 2)
    g1 = addEdge(g1, 2, 3)
    g1 = addEdge(g1, 3, 0)
    g1 = addEdge(g1, 2, 4)
    g1 = addEdge(g1, 4, 2)
    #print(g1)
 
    print("Yes" if isSC(g1, 5) else "No")
 
    g2 = [[] for i in range(4)]
 
    g2 = addEdge(g2, 0, 1)
    g2 = addEdge(g2, 1, 2)
    g2 = addEdge(g2, 2, 3)
 
    print("Yes" if isSC(g2, 4) else "No")
 
# This code is contributed by mohit kumar 29

Yes
No

Complejidad de tiempo: la complejidad de tiempo de la implementación anterior es la misma que la búsqueda primero en amplitud, que es O (V + E) si el gráfico se representa mediante una representación de array de adyacencia.

¿Podemos mejorar más?  
El enfoque anterior requiere dos recorridos del gráfico. Podemos encontrar si un gráfico está fuertemente conectado o no en un recorrido utilizando el algoritmo de Tarjan para encontrar componentes fuertemente conectados .

Este artículo es una contribución de Shivam Pradhan (anuj_charm) . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.