Una estructura de datos de conjunto disjunto es una estructura de datos que realiza un seguimiento de un conjunto de elementos divididos en varios subconjuntos disjuntos (que no se superponen). Un algoritmo de búsqueda de unión es un algoritmo que realiza dos operaciones útiles en una estructura de datos de este tipo:
- Buscar: determina en qué subconjunto se encuentra un elemento en particular. Esto se puede usar para determinar si dos elementos están en el mismo subconjunto.
- Unión: unir dos subconjuntos en un solo subconjunto. Aquí primero tenemos que verificar si los dos subconjuntos pertenecen al mismo conjunto. Si no, entonces no podemos realizar la unión.
En esta publicación, discutiremos la aplicación de la estructura de datos de conjuntos disjuntos. La aplicación es para comprobar si un gráfico dado contiene un ciclo o no.
El algoritmo Union-Find se puede usar para verificar si un gráfico no dirigido contiene un ciclo o no. Tenga en cuenta que hemos discutido un algoritmo para detectar el ciclo . Este es otro método basado en Union-Find . Este método asume que el gráfico no contiene bucles automáticos.
Podemos realizar un seguimiento de los subconjuntos en una array 1D, llamémoslo parent[].
Consideremos el siguiente gráfico:
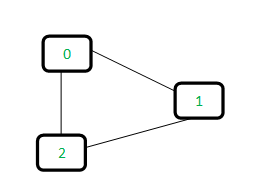
Para cada borde, haz subconjuntos usando ambos vértices del borde. Si ambos vértices están en el mismo subconjunto, se encuentra un ciclo.
Inicialmente, todas las ranuras de la array principal se inicializan en -1 (significa que solo hay un elemento en cada subconjunto).
0 1 2 -1 -1 -1
Ahora procese todos los bordes uno por uno.
Arista 0-1: Encuentra los subconjuntos en los que están los vértices 0 y 1. Como están en diferentes subconjuntos, tomamos la unión de ellos. Para tomar la unión, haga que el Node 0 sea padre del Node 1 o viceversa.
0 1 2 <----- 1 is made parent of 0 (1 is now representative of subset {0, 1})
1 -1 -1
Edge 1-2: 1 está en el subconjunto 1 y 2 está en el subconjunto 2. Entonces, tome la unión.
0 1 2 <----- 2 is made parent of 1 (2 is now representative of subset {0, 1, 2})
1 2 -1
Edge 0-2: 0 está en el subconjunto 2 y 2 también está en el subconjunto 2. Por lo tanto, incluir este borde forma un ciclo.
¿Cómo el subconjunto de 0 es igual a 2?
0->1->2 // 1 es padre de 0 y 2 es padre de 1
Basado en la explicación anterior, a continuación se muestran las implementaciones:
C++
// A union-find algorithm to detect cycle in a graph
#include <bits/stdc++.h>
using namespace std;
// a structure to represent an edge in graph
class Edge
{
public:
int src, dest;
};
// a structure to represent a graph
class Graph
{
public:
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges
Edge* edge;
};
// Creates a graph with V vertices and E edges
Graph* createGraph(int V, int E)
{
Graph* graph = new Graph();
graph->V = V;
graph->E = E;
graph->edge = new Edge[graph->E * sizeof(Edge)];
return graph;
}
// A utility function to find the subset of an element i
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// A utility function to do union of two subsets
void Union(int parent[], int x, int y)
{
parent[x] = y;
}
// The main function to check whether a given graph contains
// cycle or not
int isCycle(Graph* graph)
{
// Allocate memory for creating V subsets
int* parent = new int[graph->V * sizeof(int)];
// Initialize all subsets as single element sets
memset(parent, -1, sizeof(int) * graph->V);
// Iterate through all edges of graph, find subset of
// both vertices of every edge, if both subsets are
// same, then there is cycle in graph.
for (int i = 0; i < graph->E; ++i) {
int x = find(parent, graph->edge[i].src);
int y = find(parent, graph->edge[i].dest);
if (x == y)
return 1;
Union(parent, x, y);
}
return 0;
}
// Driver code
int main()
{
/* Let us create the following graph
0
| \
| \
1---2 */
int V = 3, E = 3;
Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// add edge 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
cout << "graph contains cycle";
else
cout << "graph doesn't contain cycle";
return 0;
}
// This code is contributed by rathbhupendra
C
// A union-find algorithm to detect cycle in a graph
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// a structure to represent an edge in graph
struct Edge
{
int src, dest;
};
// a structure to represent a graph
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph =
(struct Graph*) malloc( sizeof(struct Graph) );
graph->V = V;
graph->E = E;
graph->edge =
(struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
return graph;
}
// A utility function to find the subset of an element i
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// A utility function to do union of two subsets
void Union(int parent[], int x, int y)
{
parent[x] = y;
}
// The main function to check whether a given graph contains
// cycle or not
int isCycle( struct Graph* graph )
{
// Allocate memory for creating V subsets
int *parent = (int*) malloc( graph->V * sizeof(int) );
// Initialize all subsets as single element sets
memset(parent, -1, sizeof(int) * graph->V);
// Iterate through all edges of graph, find subset of both
// vertices of every edge, if both subsets are same, then
// there is cycle in graph.
for(int i = 0; i < graph->E; ++i)
{
int x = find(parent, graph->edge[i].src);
int y = find(parent, graph->edge[i].dest);
if (x == y)
return 1;
Union(parent, x, y);
}
return 0;
}
// Driver program to test above functions
int main()
{
/* Let us create the following graph
0
| \
| \
1---2 */
int V = 3, E = 3;
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// add edge 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
printf( "graph contains cycle" );
else
printf( "graph doesn't contain cycle" );
return 0;
}
Java
// Java Program for union-find algorithm to detect cycle in a graph
import java.util.*;
import java.lang.*;
import java.io.*;
class Graph
{
int V, E; // V-> no. of vertices & E->no.of edges
Edge edge[]; // /collection of all edges
class Edge
{
int src, dest;
};
// Creates a graph with V vertices and E edges
Graph(int v,int e)
{
V = v;
E = e;
edge = new Edge[E];
for (int i=0; i<e; ++i)
edge[i] = new Edge();
}
// A utility function to find the subset of an element i
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// A utility function to do union of two subsets
void Union(int parent[], int x, int y)
{
parent[x] = y;
}
// The main function to check whether a given graph
// contains cycle or not
int isCycle( Graph graph)
{
// Allocate memory for creating V subsets
int parent[] = new int[graph.V];
// Initialize all subsets as single element sets
for (int i=0; i<graph.V; ++i)
parent[i]=-1;
// Iterate through all edges of graph, find subset of both
// vertices of every edge, if both subsets are same, then
// there is cycle in graph.
for (int i = 0; i < graph.E; ++i)
{
int x = graph.find(parent, graph.edge[i].src);
int y = graph.find(parent, graph.edge[i].dest);
if (x == y)
return 1;
graph.Union(parent, x, y);
}
return 0;
}
// Driver Method
public static void main (String[] args)
{
/* Let us create the following graph
0
| \
| \
1---2 */
int V = 3, E = 3;
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
// add edge 1-2
graph.edge[1].src = 1;
graph.edge[1].dest = 2;
// add edge 0-2
graph.edge[2].src = 0;
graph.edge[2].dest = 2;
if (graph.isCycle(graph)==1)
System.out.println( "graph contains cycle" );
else
System.out.println( "graph doesn't contain cycle" );
}
}
Python3
# Python Program for union-find algorithm to detect cycle in a undirected graph
# we have one egde for any two vertex i.e 1-2 is either 1-2 or 2-1 but not both
from collections import defaultdict
#This class represents a undirected graph using adjacency list representation
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# A utility function to find the subset of an element i
def find_parent(self, parent,i):
if parent[i] == -1:
return i
if parent[i]!= -1:
return self.find_parent(parent,parent[i])
# A utility function to do union of two subsets
def union(self,parent,x,y):
parent[x] = y
# The main function to check whether a given graph
# contains cycle or not
def isCyclic(self):
# Allocate memory for creating V subsets and
# Initialize all subsets as single element sets
parent = [-1]*(self.V)
# Iterate through all edges of graph, find subset of both
# vertices of every edge, if both subsets are same, then
# there is cycle in graph.
for i in self.graph:
for j in self.graph[i]:
x = self.find_parent(parent, i)
y = self.find_parent(parent, j)
if x == y:
return True
self.union(parent,x,y)
# Create a graph given in the above diagram
g = Graph(3)
g.addEdge(0, 1)
g.addEdge(1, 2)
g.addEdge(2, 0)
if g.isCyclic():
print ("Graph contains cycle")
else :
print ("Graph does not contain cycle ")
#This code is contributed by Neelam Yadav
C#
// C# Program for union-find
// algorithm to detect cycle
// in a graph
using System;
class Graph{
// V-> no. of vertices &
// E->no.of edges
public int V, E;
// collection of all edges
public Edge []edge;
class Edge
{
public int src, dest;
};
// Creates a graph with V
// vertices and E edges
public Graph(int v,int e)
{
V = v;
E = e;
edge = new Edge[E];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
// A utility function to find
// the subset of an element i
int find(int []parent, int i)
{
if (parent[i] == -1)
return i;
return find(parent,
parent[i]);
}
// A utility function to do
// union of two subsets
void Union(int []parent,
int x, int y)
{
parent[x] = y;
}
// The main function to check
// whether a given graph
// contains cycle or not
int isCycle(Graph graph)
{
// Allocate memory for
// creating V subsets
int []parent =
new int[graph.V];
// Initialize all subsets as
// single element sets
for (int i = 0; i < graph.V; ++i)
parent[i] =- 1;
// Iterate through all edges of graph,
// find subset of both vertices of every
// edge, if both subsets are same, then
// there is cycle in graph.
for (int i = 0; i < graph.E; ++i)
{
int x = graph.find(parent,
graph.edge[i].src);
int y = graph.find(parent,
graph.edge[i].dest);
if (x == y)
return 1;
graph.Union(parent, x, y);
}
return 0;
}
// Driver code
public static void Main(String[] args)
{
/* Let us create the following graph
0
| \
| \
1---2 */
int V = 3, E = 3;
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
// add edge 1-2
graph.edge[1].src = 1;
graph.edge[1].dest = 2;
// add edge 0-2
graph.edge[2].src = 0;
graph.edge[2].dest = 2;
if (graph.isCycle(graph) == 1)
Console.WriteLine("graph contains cycle");
else
Console.WriteLine("graph doesn't contain cycle");
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// Javascript program for union-find
// algorithm to detect cycle
// in a graph
// V-> no. of vertices &
// E->no.of edges
var V, E;
// Collection of all edges
var edge;
class Edge
{
constructor()
{
this.src = 0;
this.dest = 0;
}
};
// Creates a graph with V
// vertices and E edges
function initialize(v,e)
{
V = v;
E = e;
edge = Array.from(Array(E), () => Array());
}
// A utility function to find
// the subset of an element i
function find(parent, i)
{
if (parent[i] == -1)
return i;
return find(parent,
parent[i]);
}
// A utility function to do
// union of two subsets
function Union(parent, x, y)
{
parent[x] = y;
}
// The main function to check
// whether a given graph
// contains cycle or not
function isCycle()
{
// Allocate memory for
// creating V subsets
var parent = Array(V).fill(0);
// Initialize all subsets as
// single element sets
for(var i = 0; i < V; ++i)
parent[i] =- 1;
// Iterate through all edges of graph,
// find subset of both vertices of every
// edge, if both subsets are same, then
// there is cycle in graph.
for (var i = 0; i < E; ++i)
{
var x = find(parent,
edge[i].src);
var y = find(parent,
edge[i].dest);
if (x == y)
return 1;
Union(parent, x, y);
}
return 0;
}
// Driver code
/* Let us create the following graph
0
| \
| \
1---2 */
var V = 3, E = 3;
initialize(V, E);
// Add edge 0-1
edge[0].src = 0;
edge[0].dest = 1;
// Add edge 1-2
edge[1].src = 1;
edge[1].dest = 2;
// Add edge 0-2
edge[2].src = 0;
edge[2].dest = 2;
if (isCycle() == 1)
document.write("graph contains cycle");
else
document.write("graph doesn't contain cycle");
// This code is contributed by rutvik_56
</script>
graph contains cycle
Tenga en cuenta que la implementación de union() y find() es ingenua y toma O(n) tiempo en el peor de los casos. Estos métodos se pueden mejorar a O(Logn) usando Union by Rank o Height . Pronto estaremos discutiendo Union by Rank en una publicación separada.
Artículos relacionados:
Algoritmo de búsqueda de unión | Conjunto 2 (Unión por rango y compresión de rutas)
Estructuras de datos de conjuntos disjuntos (Implementación de Java)
Algoritmos codiciosos | Conjunto 2 (algoritmo de árbol de expansión mínimo de Kruskal)
Problema de secuenciación de tareas | Conjunto 2 (usando conjunto disjunto)
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA