En teoría de grafos, un conjunto dominante para un gráfico G = (V, E) es un subconjunto D de V tal que cada vértice que no está en D es adyacente a al menos un miembro de D. El número de dominación es el número de vértices en un conjunto dominante más pequeño para G. 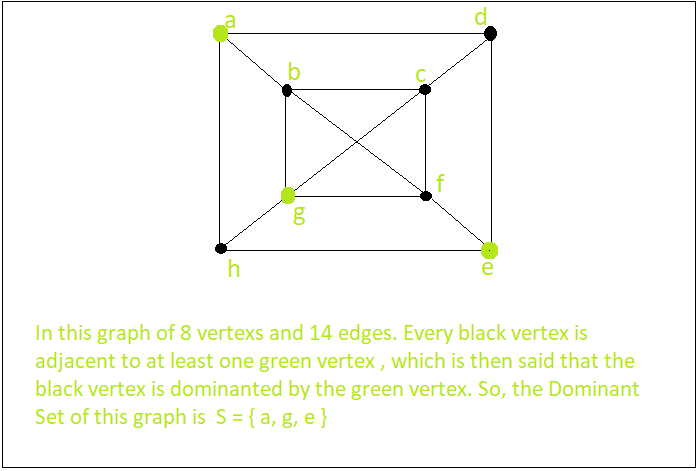
Ejemplos:
Input : A graph with 4 vertex and 4 edgesOutput : The Dominant Set S= { a, b } or { a, d } or { a, c } and more. Input : A graph with 6 vertex and 7 edges
Output : The Dominant Set S= { a, d, f } or { e, c } and more.
Se cree que puede no haber un algoritmo eficiente que encuentre un conjunto dominante más pequeño para todos los gráficos, pero existen algoritmos de aproximación eficientes.
Algoritmo:
- Primero tenemos que inicializar un conjunto ‘S’ como vacío
- Tome cualquier borde ‘e’ del gráfico que conecta los vértices (digamos A y B)
- Agregue un vértice entre A y B (digamos A) a nuestro conjunto S
- Eliminar todos los bordes en el gráfico conectado a A
- Regrese al paso 2 y repita, si aún queda algún borde en el gráfico
- El conjunto final S es un Conjunto Dominante del grafo
C++
// C++ program to find the Dominant Set of a graph
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > g;
bool box[100000];
vector<int> Dominant(int ver, int edge)
{
vector<int> S; // set S
for (int i = 0; i < ver; i++) {
if (!box[i]) {
S.push_back(i);
box[i] = true;
for (int j = 0; j < (int)g[i].size(); j++) {
if (!box[g[i][j]]) {
box[g[i][j]] = true;
break;
}
}
}
}
return S;
}
// Driver function
int main()
{
int ver, edge, x, y;
ver = 5; // Enter number of vertices
edge = 6; // Enter number of Edges
g.resize(ver);
// Setting all index value of an array as 0
memset(box, 0, sizeof(box));
// Enter all the end-points of all the Edges
// g[x--].push_back[y--] g[y--].push_back[x--]
g[0].push_back(1);
g[1].push_back(0); // x = 1, y = 2 ;
g[1].push_back(2);
g[2].push_back(1); // x = 2, y = 3 ;
g[2].push_back(3);
g[3].push_back(2); // x = 3, y = 4 ;
g[0].push_back(3);
g[3].push_back(0); // x = 1, y = 4 ;
g[3].push_back(4);
g[4].push_back(3); // x = 4, y = 5 ;
g[2].push_back(4);
g[4].push_back(2); // x = 3, y = 5 ;
vector<int> S = Dominant(ver, edge);
cout << "The Dominant Set is : { ";
for (int i = 0; i < (int)S.size(); i++)
cout << S[i] + 1 << " ";
cout << "}";
return 0;
}
Java
// Java program to find the Dominant Set of a graph
import java.util.*;
class GFG
{
static Vector<Integer> []g;
static boolean []box = new boolean[100000];
static Vector<Integer> Dominant(int ver, int edge)
{
Vector<Integer> S = new Vector<Integer>(); // set S
for (int i = 0; i < ver; i++)
{
if (!box[i])
{
S.add(i);
box[i] = true;
for (int j = 0; j < (int)g[i].size(); j++)
{
if (!box[g[i].get(j)])
{
box[g[i].get(j)] = true;
break;
}
}
}
}
return S;
}
// Driver code
public static void main(String[] args)
{
int ver, edge, x, y;
ver = 5; // Enter number of vertices
edge = 6; // Enter number of Edges
g = new Vector[ver];
for (int i = 0; i < ver; i++)
g[i] = new Vector<Integer>();
// Enter all the end-points of all the Edges
// g[x--].push_back[y--] g[y--].push_back[x--]
g[0].add(1);
g[1].add(0); // x = 1, y = 2 ;
g[1].add(2);
g[2].add(1); // x = 2, y = 3 ;
g[2].add(3);
g[3].add(2); // x = 3, y = 4 ;
g[0].add(3);
g[3].add(0); // x = 1, y = 4 ;
g[3].add(4);
g[4].add(3); // x = 4, y = 5 ;
g[2].add(4);
g[4].add(2); // x = 3, y = 5 ;
Vector<Integer> S = Dominant(ver, edge);
System.out.print("The Dominant Set is : { ");
for (int i = 0; i < (int)S.size(); i++)
System.out.print(S.get(i) + 1 + " ");
System.out.print("}");
}
}
// This code is contributed by Rajput-Ji
C#
// C# program to find the Dominant Set of a graph
using System;
using System.Collections.Generic;
class GFG
{
static List<int> []g;
static bool []box = new bool[100000];
static List<int> Dominant(int ver, int edge)
{
List<int> S = new List<int>(); // set S
for (int i = 0; i < ver; i++)
{
if (!box[i])
{
S.Add(i);
box[i] = true;
for (int j = 0; j < (int)g[i].Count; j++)
{
if (!box[g[i][j]])
{
box[g[i][j]] = true;
break;
}
}
}
}
return S;
}
// Driver code
public static void Main(String[] args)
{
int ver, edge;
ver = 5; // Enter number of vertices
edge = 6; // Enter number of Edges
g = new List<int>[ver];
for (int i = 0; i < ver; i++)
g[i] = new List<int>();
// Enter all the end-points of all the Edges
// g[x--].push_back[y--] g[y--].push_back[x--]
g[0].Add(1);
g[1].Add(0); // x = 1, y = 2 ;
g[1].Add(2);
g[2].Add(1); // x = 2, y = 3 ;
g[2].Add(3);
g[3].Add(2); // x = 3, y = 4 ;
g[0].Add(3);
g[3].Add(0); // x = 1, y = 4 ;
g[3].Add(4);
g[4].Add(3); // x = 4, y = 5 ;
g[2].Add(4);
g[4].Add(2); // x = 3, y = 5 ;
List<int> S = Dominant(ver, edge);
Console.Write("The Dominant Set is : { ");
for (int i = 0; i < (int)S.Count; i++)
Console.Write(S[i] + 1 + " ");
Console.Write("}");
}
}
// This code is contributed by PrinciRaj1992
Producción:
The Dominant Set is : { 1 3 5 }
Referencia: wiki
Publicación traducida automáticamente
Artículo escrito por AmanSrivastava1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA