Suponga que un camión rápido choca con un automóvil detenido, lo que hace que el automóvil comience a moverse. ¿Qué está pasando exactamente detrás de escena? En este caso, a medida que la velocidad del camión disminuye, la velocidad del automóvil aumenta y, por lo tanto, el impulso perdido por el camión es adquirido por el automóvil. ¿Qué piensas? Aprendamos más sobre el impulso y su discusión a continuación:
¿Qué es Momentum?
Momentum o momento lineal se define como el producto de la masa de un objeto y su velocidad. O, en otras palabras, el impulso se denomina «masa en movimiento». Debido a que todos los objetos tienen masa, si un objeto se mueve, tiene cantidad de movimiento, su masa está en movimiento.
Cualquier cambio en la masa o la velocidad del sistema provoca un cambio en el momento lineal. La masa de un objeto y la velocidad son directamente proporcionales al momento lineal. El momento lineal se puede expresar como:
Momento = masa × velocidad
o
pags = metro × v
donde p es el momento lineal, m es la masa y v es la velocidad del objeto.
A partir de esto, se puede concluir que cuanto mayor sea la masa del objeto o la velocidad, mayor será el momento lineal.
La cantidad de movimiento es una cantidad vectorial porque tiene dirección y magnitud. Su dirección es la misma que la de la velocidad.
El kilogramo-metro-por-segundo es la unidad SI de momento ( kg m/s ).
Gráficamente, la relación entre masa y velocidad en términos de cantidad de movimiento se puede trazar como:
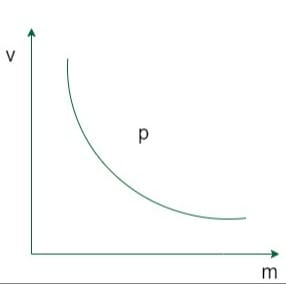
Como la aplicación de una fuerza desequilibrada provoca un cambio en la velocidad del objeto, se deduce que una fuerza también provoca un cambio en la cantidad de movimiento. La cantidad de movimiento al comienzo del intervalo de tiempo se define como la cantidad de movimiento inicial , y la cantidad de movimiento al final del intervalo de tiempo se define como la cantidad de movimiento final .
Leyes del movimiento
Las tres leyes del movimiento proporcionadas por Newton se enuncian a continuación:
- Primera ley del movimiento: esta ley también se denomina ley de la inercia y se establece como: un cuerpo continúa en estado de reposo o en movimiento a menos que sea obligado por alguna fuerza externa.
- Segunda ley del movimiento: De acuerdo con la segunda ley del movimiento de Newton, la tasa de cambio de la cantidad de movimiento de un cuerpo es directamente proporcional a la fuerza externa aplicada sobre él y el cambio tiene lugar en la dirección de la fuerza aplicada.
- Tercera Ley del Movimiento: De acuerdo con la Tercera Ley del Movimiento de Newton, Por cada acción, hay una reacción igual y opuesta, y actúan sobre dos cuerpos diferentes. Las fuerzas de acción y reacción son iguales y opuestas, y actúan sobre dos cuerpos diferentes.
La ley de conservación del momento lineal es un resultado significativo de la tercera ley del movimiento de Newton de acuerdo con la segunda ley del movimiento.
Ley de Conservación del Momento
El principio de conservación de la cantidad de movimiento establece que si dos objetos chocan, la cantidad de movimiento total antes y después de la colisión será la misma si ninguna fuerza externa actúa sobre los objetos que chocan. O simplemente se puede expresar como:
Si no hay una fuerza externa que actúe sobre el sistema, la cantidad de movimiento es constante. Cuando dos objetos chocan en un sistema aislado, la cantidad de movimiento total de los dos objetos antes de la colisión es igual a la cantidad de movimiento total de los dos objetos después de la colisión.
Cuando la fuerza externa neta es cero, la cantidad de movimiento del sistema permanece constante, como se expresa matemáticamente mediante la fórmula de conservación de la cantidad de movimiento lineal.
Momento final (P f ) = Momento inicial (P i )
De esto se puede interpretar que, para dos o más cuerpos cualesquiera en un sistema aislado que actúan uno sobre el otro, su cantidad de movimiento total permanece constante a menos que se aplique una fuerza externa. Por lo tanto, se puede decir que el impulso no puede crearse ni destruirse. Esta ley es válida sólo para el movimiento lineal. Las fuerzas internas no pueden cambiar el momento total del sistema, sin embargo, pueden cambiar el momento de cada partícula del sistema.
Por ejemplo, en un cohete, el combustible se quema debido a que los gases se expulsan hacia abajo. Entonces el cohete se mueve hacia arriba para conservar el impulso. El combustible en un avión a reacción se quema y expulsa gases en dirección hacia atrás. Por lo tanto, por conservación de la cantidad de movimiento, el avión avanza.
Derivación de la conservación de la cantidad de movimiento
Consideremos dos cuerpos A y B con velocidades iniciales u 1 y u 2 respectivamente. Después de algún tiempo, sufren colisión. Después del choque, las velocidades de A y B serán v 1 y v 2 . Sean el tiempo de contacto entre dos cuerpos t y m 1 y m 2 las masas de los cuerpos A y B respectivamente.
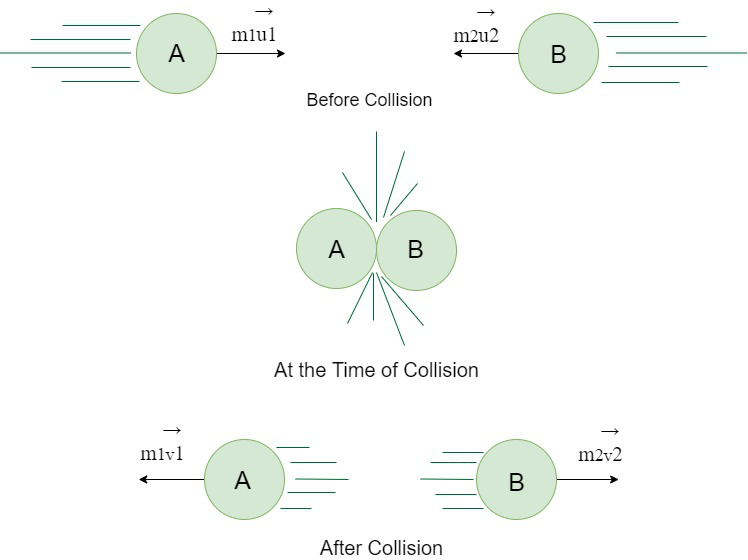
Representación pictórica para la conservación del momento
Calculemos el cambio en la cantidad de movimiento para el cuerpo A y está representado por p A y está dado por,
pags UNA = metro 1 (v 1 – tu 1 )
Calculemos el cambio de cantidad de movimiento para el cuerpo B y está representado por p B y viene dado por,
pags segundo = metro 2 ( v 2 – tu 2 )
Ahora, a partir de la Tercera Ley del Movimiento de Newton se puede escribir como,
F AB = -F BA ……(1)
donde F AB es la fuerza que actúa sobre A debido a B y F BA es la fuerza que actúa sobre B debido a A.
Ahora, a partir de la Segunda Ley del Movimiento de Newton se puede escribir como,
F AB = m 1 a 1 y ……(2)
F BA = metro 2 un 2 ……(3)
donde a 1 y a 2 son las aceleraciones de los cuerpos A y B.
Por lo tanto, sustituya la ecuación (2) y (3) en la ecuación (1) como,
metro 1 un 1 = metro 2 un 2
Por lo tanto, esto implica que,
metro 1 (v 1 – tu 1 ) / t = metro 2 (v 2 – tu 2 ) / t
metro 1 (v 1 – tu 1 ) = metro 2 (v 2 – tu 2 )
metro 1 tu 1 + metro 2 tu 2 = metro 1 v 1 + metro 2 v 2 ……(4)
esta ecuación (4) representa la ecuación de la ley de conservación del momento.
donde LHS representa la cantidad de movimiento total de los cuerpos A y B antes de la colisión y RHS representa la cantidad de movimiento total de los cuerpos A y B después de la colisión.
Por lo tanto, de esto se concluye que se conserva la cantidad de movimiento .
Problemas de muestra
Problema 1: Un cuerpo de 10 kg de masa se acelera uniformemente desde una velocidad de 5 m/s hasta 10 m/s en 5 s. Calcular la cantidad de movimiento inicial y final del cuerpo. Además, encuentre la magnitud de la fuerza que actúa sobre ese cuerpo.
Solución:
Dado
Masa del cuerpo, m = 10 kg.
Velocidad inicial del cuerpo, u = 5 m/s.
Velocidad final del cuerpo, v = 10 m/s.
Tiempo que tarda ese cuerpo, t = 5 s.
Por lo tanto,
Momento inicial del cuerpo, p i = m × u
= 10 kg × 5 m/s
= 50 kg ms- 1
Momento final del cuerpo, p f = m×v
= 10 kg × 10 ms -1
= 100 kg ms- 1
Fuerza que actúa sobre ese cuerpo, F = m × (vu) / t
= 10 × (10 – 5) / 5
= 10N
El momento inicial y el momento final y la fuerza que actúan sobre ese cuerpo son 50 kg ms -1 y 100 kg ms -1 y 10 N respectivamente.
Problema 2: Una fuerza produce una aceleración de 16 m/s 2 en una masa de 0,5 kg y una aceleración de 4,0 m/s 2 en una masa desconocida cuando se aplica por separado. Si ambas masas están unidas, ¿cuál será la aceleración bajo la misma fuerza?
Solución:
Dado que,
Masa del primer objeto = 0,5 kg
Aceleración que actúa sobre el primer objeto = 16 m/s 2
Sea m la masa del segundo objeto.
Aceleración que actúa sobre el segundo objeto = 4 m/s 2
Calculemos la fuerza que actúa sobre el primer objeto y sea F
Lo sabemos
Fuerza, F = m × a ……(1)
donde m y a son la masa y la aceleración del cuerpo.
F = 0,5 × 16
= 8 norte
Dado que ambos objetos están unidos, la fuerza que actúa sobre ambos objetos es la misma.
Calculemos la masa del segundo cuerpo a partir de (1)
m = F/a
8/4 = 2 kg
Por lo tanto, Masa del segundo cuerpo = 2 kg
Sea 1 la aceleración que actúa sobre ambos objetos cuando ambos objetos están atados y la Fuerza F actúa sobre ellos.
un 1 = F / (m + m 1 )
= 8/(0,5+2)
= 8/2,5
= 3,2 m/ s2
Por tanto, la aceleración bajo la misma fuerza será de 3,2 m/s 2 .
Problema 3: Un automóvil tiene una aceleración de 20 m/s 2 y después de un tiempo acelera a 40 m/s 2 ¿cuál es la relación de fuerza ejercida por los motores?
Solución:
Dado que,
La aceleración inicial, a 1 = 20 m/s 2
La aceleración final, a 2 = 40 m/s 2
Por lo tanto, la fuerza inicial y final es,
F 1 = metro × un 1
F 2 = metro × un 2
Y sus proporciones es,
F 1 /F 2 = metro × un 1 / metro × un 2
F 1 / F 2 = un 1 / un 2
F 1 /F 2 = 20/40
F1 :F2 = 1 : 2
Problema 4: ¿Cuál será la aceleración cuando se apliquen 20 N de fuerza sobre un bloque de 100 kg?
Solución:
Dado que,
La fuerza, F = 20 N.
La masa del bloque, m = 100 kg.
Como la fuerza se define como,
F = mxa
20 N = 100 kg x
a = 20 N /100 kg
= 0,002 m/ s2
Entonces, la aceleración es 2 x 10 -3 m/s 2
Problema 5: Si se aplica constantemente una fuerza constante de 5 N sobre un bloque de 5 kg, ¿cuánto será la aceleración del bloque?
Solución:
Dado que,
La fuerza, F = 5 N.
La Masa, m = 5 kg.
La velocidad inicial, u = 0 m/s 2 .
La velocidad final, v = 20 m/s 2
Ya que,
F = mamá
o
a = F/m
Por lo tanto,
a = 5 N / 5 kg
= 1 m/s 2
Publicación traducida automáticamente
Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA