Construcción del árbol de sufijos de Ukkonen – Parte 3

Este artículo es la continuación de dos artículos siguientes:
Construcción del árbol de sufijos de Ukkonen – Parte 1
Construcción del árbol de sufijos de Ukkonen – Parte 2

Lea la Parte 1 y la Parte 2 antes de ver el artículo actual, donde hemos visto algunos conceptos básicos sobre el árbol de sufijos, el algoritmo de ukkonen de alto nivel, el enlace de sufijos y tres trucos de implementación.

Aquí tomaremos la string S = «abcabxabcd» como ejemplo y revisaremos todas las cosas paso a paso y crearemos el árbol.
Agregaremos $(discutido en la Parte 1 por qué hacemos esto) para que la string S sea «abcabxabcd$».

Al construir el árbol de sufijos para la string S de longitud m:

• Habrá m fases 1 a m (una fase para cada carácter)
  En nuestro ejemplo actual, m es 11, por lo que habrá 11 fases.
• La primera fase agregará el primer carácter ‘a’ en el árbol, la segunda fase agregará el segundo carácter ‘b’ en el árbol, la tercera fase agregará el tercer carácter ‘c’ en el árbol, ……, la m ^-ésima fase agregará el m ^-ésimo carácter en el árbol (Esto hace que el algoritmo de Ukkonen sea un algoritmo en línea)
• Cada fase i pasará como máximo por i extensiones (de 1 a i). Si el carácter actual que se está agregando en el árbol no se ve hasta el momento, todas las extensiones i se completarán (la regla de extensión 3 no se aplicará en esta fase). Si el carácter actual que se agrega en el árbol se ve antes, entonces la fase i se completará antes (tan pronto como se aplique la regla de extensión 3) sin pasar por todas las extensiones i
• Hay tres reglas de extensión (1, 2 y 3) y cada extensión j (de 1 a i) de cualquier fase i se adherirá a una de estas tres reglas.
• La regla 1 agrega un nuevo carácter en el borde de la hoja existente
• La regla 2 crea un nuevo borde de hoja (y también puede crear un nuevo Node interno, si la etiqueta de ruta termina entre un borde)
• La regla 3 finaliza la fase actual (cuando se encuentra el carácter actual en el borde actual que se está atravesando)
• La fase 1 leerá el primer carácter de la string, pasará por 1 extensión.
  (En las figuras, mostramos los caracteres en las etiquetas de los bordes solo como explicación, mientras escribimos el código, solo usaremos los índices de inicio y fin; la compresión de etiquetas de los bordes discutida en la Parte 2 )
  La extensión 1 agregará el sufijo «a» en el árbol. Comenzamos desde la raíz y recorremos la ruta con la etiqueta ‘a’. No hay camino desde la raíz, saliendo con la etiqueta ‘a’, así que cree un borde de hoja (Regla 2).
  
  La Fase 1 se completa con la finalización de la extensión 1 (Como una fase i tiene como máximo i extensiones)
  Para cualquier string, la Fase 1 tendrá solo una extensión y siempre seguirá la Regla 2.
• La fase 2 leerá el segundo carácter, pasará por al menos 1 y como máximo 2 extensiones.
  En nuestro ejemplo, la fase 2 leerá el segundo carácter ‘b’. Los sufijos que se agregarán son «ab» y «b».
  La extensión 1 agrega el sufijo «ab» en el árbol.
  La ruta para la etiqueta ‘a’ termina en el borde de la hoja, así que agregue ‘b’ al final de este borde.
  La extensión 1 solo incrementa el índice final en 1 (de 1 a 2) en el primer borde (Regla 1).
  
  La extensión 2 agrega el sufijo «b» en el árbol. No hay ruta desde la raíz, saliendo con la etiqueta ‘b’, por lo que crea un borde de hoja (Regla 2).
  
  La Fase 2 se completa con la finalización de la extensión 2.
  La Fase 2 pasó por dos extensiones aquí. Regla 1 aplicada en 1ra Ampliación y Regla 2 aplicada en 2da Ampliación.
• La fase 3 leerá el tercer carácter, pasará por al menos 1 y como máximo 3 extensiones.
  En nuestro ejemplo, la fase 3 leerá el tercer carácter ‘c’. Los sufijos que se agregarán son «abc», «bc» y «c».
  La extensión 1 agrega el sufijo «abc» en el árbol.
  La ruta para la etiqueta ‘ab’ termina en el borde de la hoja, así que agregue ‘c’ al final de este borde.
  La extensión 1 simplemente incrementa el índice final en 1 (de 2 a 3) en este borde (Regla 1).
  
  La extensión 2 agrega el sufijo «bc» en el árbol.
  La ruta para la etiqueta ‘b’ termina en el borde de la hoja, así que agregue ‘c’ al final de este borde.
  La extensión 2 simplemente incrementa el índice final en 1 (de 2 a 3) en este borde (Regla 1).
  
  La extensión 3 agrega el sufijo «c» en el árbol. No hay camino desde la raíz, saliendo con la etiqueta ‘c’, por lo que crea un borde de hoja (Regla 2).
  
  La Fase 3 se completa con la finalización de la extensión 3.
  La Fase 3 pasó por tres extensiones aquí. La regla 1 se aplicó en las dos primeras prórrogas y la regla 2 se aplicó en la 3ra prórroga.
• La fase 4 leerá el cuarto carácter, irá a por lo menos 1 y como máximo a 4 extensiones.
  En nuestro ejemplo, la fase 4 leerá el cuarto carácter ‘a’. Los sufijos que se agregarán son «abca», «bca», «ca» y «a».
  La extensión 1 agrega el sufijo «abca» en el árbol.
  La ruta para la etiqueta ‘abc’ termina en el borde de la hoja, así que agregue ‘a’ al final de este borde.
  La extensión 1 simplemente incrementa el índice final en 1 (de 3 a 4) en este borde (Regla 1).
  
  La extensión 2 agrega el sufijo «bca» en el árbol.
  La ruta para la etiqueta ‘bc’ termina en el borde de la hoja, así que agregue ‘a’ al final de este borde.
  La extensión 2 solo incrementa el índice final en 1 (de 3 a 4) en este borde (Regla 1).
  
  La extensión 3 agrega el sufijo «ca» en el árbol.
  La ruta para la etiqueta ‘c’ termina en el borde de la hoja, así que agregue ‘a’ al final de este borde.
  La extensión 3 simplemente incrementa el índice final en 1 (de 3 a 4) en este borde (Regla 1).
  
  La extensión 4 agrega el sufijo «a» en el árbol.
  La ruta para la etiqueta ‘a’ existe en el árbol. No se necesita más trabajo y la Fase 4 termina aquí (Regla 3 y Truco 2). Este es un ejemplo de árbol de sufijos implícitos. Aquí el sufijo “a” no se ve explícitamente (porque no termina en el borde de una hoja) pero está en el árbol implícitamente. Por lo tanto, no hay cambios en la estructura del árbol después de la extensión 4. Permanecerá como se muestra arriba en la Figura 28.
  La Fase 4 se completa tan pronto como se aplica la Regla 3 mientras que la Extensión 4.
  La Fase 4 pasó por cuatro extensiones aquí. La regla 1 se aplicó en las tres primeras prórrogas y la regla 3 se aplicó en la 4ª prórroga.

Ahora veremos algunas observaciones y cómo implementarlas.

1. Al final de cualquier fase i, hay como máximo i bordes de hoja (si el i ^-ésimo carácter no se ve hasta ahora, habrá i bordes de hoja, de lo contrario habrá menos de i bordes de hoja).
   Por ejemplo, después de las fases 1, 2 y 3 en nuestro ejemplo, hay 1, 2 y 3 bordes de hoja respectivamente, pero después de la fase 4, hay solo 3 bordes de hoja (no 4).
2. Después de completar la fase i, los índices «finales» de todos los bordes de las hojas son i. ¿Cómo implementamos esto en el código? ¿Necesitamos iterar a través de todas esas extensiones, encontrar los bordes de las hojas atravesando de raíz a hoja e incrementar el índice de «final»? La respuesta es “NO”.
   Para esto, mantendremos una variable global (digamos «FIN») y simplemente incrementaremos esta variable global «FIN» y todos los índices finales del borde de la hoja apuntarán a esta variable global. Entonces, de esta manera, si tenemos j bordes de hoja después de la fase i, entonces en la fase i+1, las primeras j extensiones (1 a j) se realizarán simplemente incrementando la variable «FIN» en 1 (FIN será i+1 al final). punto).
   Aquí acabamos de implementar el truco 3: una vez una hoja, siempre una hoja. Este truco procesa todos los bordes de la hoja j (es decir, extensión 1 a j) usando la regla 1 en un tiempo constante en cualquier fase. La regla 1 no se aplicará a las sucesivas prórrogas de la misma fase. Esto se puede verificar en las cuatro fases que discutimos anteriormente. Si la Regla 1 se aplica en alguna fase, solo se aplica en unas pocas fases iniciales de forma continua (digamos 1 a j). La regla 1 nunca se aplica más tarde en una fase determinada una vez que se aplica la regla 2 o la regla 3 en esa fase.
3. En el ejemplo explicado hasta ahora, en cada extensión (donde no se aplica el truco 3) de cualquier fase para agregar un sufijo en el árbol, estamos atravesando desde la raíz haciendo coincidir las etiquetas de ruta con el sufijo que se agrega. Si hay j bordes de hojas después de la fase i, entonces en la fase i+1, las primeras j extensiones seguirán la Regla 1 y se realizarán en tiempo constante usando el truco 3. Hay i+1-j extensiones aún por realizar. Para estas extensiones, ¿desde qué Node (raíz o algún otro Node interno) comenzar y qué ruta tomar? La respuesta a esto depende de cómo se complete la fase i anterior.
   Si la fase anterior pasé por todas las i extensiones (cuando i ^thel carácter es único hasta ahora), luego, en la siguiente fase i+1, el truco 3 se encargará de los primeros sufijos i (los bordes de las hojas i) y luego la extensión i+1 comenzará desde el Node raíz e insertará solo un carácter [( i+1) ^th ] sufijo en el árbol mediante la creación de un borde de hoja usando la Regla 2.
   Si la fase anterior i se completa antes (y esto sucederá si y solo si se aplica la regla 3, cuando el i ^-ésimo carácter ya se ha visto antes), diga en j ^extensión (es decir, la regla 3 se aplica en la extensión j ⁾ , entonces hay bordes de hoja j-1 hasta ahora.
   Indicaremos algunos hechos más (que pueden ser una repetición, pero queremos asegurarnos de que sea claro para usted en este punto) aquí en base a la discusión hasta el momento:
   • La fase 1 comienza con la regla 2, todas las demás fases comienzan con la regla 1
   • Cualquier fase termina con la Regla 2 o la Regla 3
   • Cualquier fase i puede pasar por una serie de j extensiones (1 <= j <= i). En estas extensiones j, las primeras extensiones p (0 <= p < i) seguirán la Regla 1, las siguientes extensiones q (0 <= q <= ip) seguirán la Regla 2 y las siguientes extensiones r (0 <= r <= 1) seguirá la Regla 3. El orden en que se aplican la Regla 1, la Regla 2 y la Regla 3 nunca se mezcla en una fase. Se aplican en orden de su número (si se aplican), es decir, en una fase, la Regla 1 se aplica primero, luego la Regla 2 y luego la Regla 3
   • En una fase i, p + q + r <= i
   • Al final de cualquier fase i, habrá bordes de hoja p+q y la próxima fase i+1 pasará por la Regla 1 para las primeras extensiones p+q

   En la siguiente fase i+1, el truco 3 (Regla 1) se encargará de los primeros sufijos j-1 (los bordes de las hojas j-1), luego comenzará la extensión j donde agregaremos el sufijo j ^-ésimo en el árbol. Para esto, necesitamos encontrar el mejor borde coincidente posible y luego agregar un nuevo carácter al final de ese borde. ¿Cómo encontrar el final del mejor borde coincidente? ¿Necesitamos atravesar desde el Node raíz y hacer coincidir los bordes del árbol con el sufijo j ^{-ésimo que se agrega carácter por carácter?} Esto llevará tiempo y el algoritmo general no será lineal. activePoint viene al rescate aquí.
   En la fase i anterior, mientras que la j ^-ésima extensión, el recorrido del camino terminaba en un punto (que podría ser un Node interno o algún punto en medio de un borde) donde i ^-ésimael carácter que se está agregando ya se encontró en el árbol y se aplicó la regla 3, la j ^-ésima extensión de la fase i+1 comenzará exactamente desde el mismo punto y comenzaremos a hacer coincidir la ruta con (i+1) el ^carácter . activePoint ayuda a evitar el recorrido innecesario de la ruta desde la raíz en cualquier extensión en función del conocimiento adquirido en los recorridos realizados en la extensión anterior. No se necesita atravesar en 1 ^.p extensiones donde se aplica la Regla 1. El recorrido se realiza donde se aplica la Regla 2 o la Regla 3 y ahí es donde activePoint indica el punto de inicio del recorrido donde hacemos coincidir la ruta con el carácter actual que se agrega en el árbol. La implementación se realiza de tal manera que, en cualquier extensión en la que necesitemos un recorrido, activePoint ya está configurado en la ubicación correcta (con un caso de excepción APCFALZ discutido a continuación) y al final de la extensión actual, restablecemos activePoint como corresponda para que el siguiente extensión (de la misma fase o de la siguiente fase) donde se requiere un recorrido, activePoint ya apunta al lugar correcto.

   activePoint : este podría ser el Node raíz, cualquier Node interno o cualquier punto en el medio de un borde. Este es el punto donde comienza el recorrido en cualquier extensión. Para la primera extensión de la fase 1, activePoint se establece como raíz. Otra extensión obtendrá activePoint configurado correctamente por la extensión anterior (con un caso de excepción APCFALZ discutido a continuación) y es responsabilidad de la extensión actual restablecer activePoint adecuadamente al final, para ser utilizado en la próxima extensión donde se aplica la Regla 2 o la Regla 3 ( de la misma fase o de la siguiente).
   Para lograr esto, necesitamos una forma de almacenar activePoint. Almacenaremos esto usando tres variables: activeNode , activeEdge , activeLength .
   Nodeactivo: podría ser un Node raíz o un Node interno.
   activeEdge : cuando estamos en el Node raíz o en el Node interno y necesitamos caminar hacia abajo, necesitamos saber qué borde elegir. activeEdge almacenará esa información. En caso de que activeNode en sí sea el punto desde donde comienza el recorrido, entonces activeEdge se establecerá en el siguiente carácter que se procesará en la siguiente fase.
   activeLength : Esto indica cuántos caracteres necesitamos caminar hacia abajo (en el camino representado por activeEdge) desde activeNode para llegar al activePoint donde comienza el recorrido. En caso de que activeNode en sí sea el punto desde donde comienza el recorrido, entonces activeLength será CERO.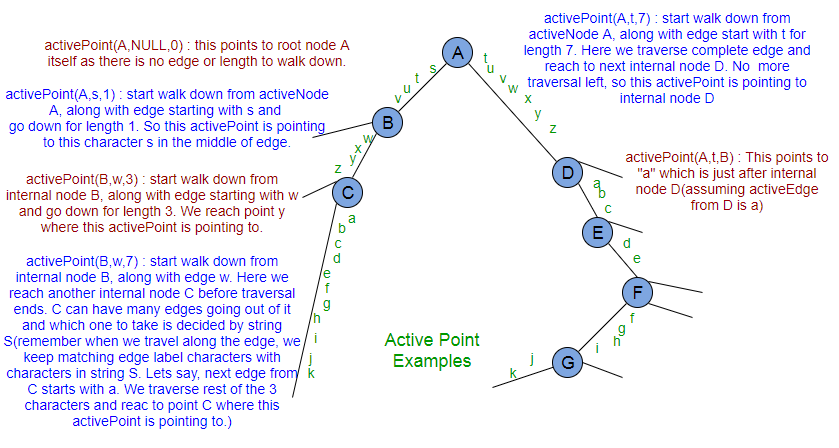
   
   Después de la fase i, si hay j bordes de hoja, entonces en la fase i+1, las primeras j extensiones se realizarán con el truco 3. Se necesitará activePoint para las extensiones de j+1 a i+1 y activePoint puede o no cambiar entre dos prórrogas según el punto donde termine la prórroga anterior.

   Cambio de activePoint para la regla de extensión 3 (APCFER3) : cuando la regla 3 se aplica en cualquier fase i, entonces, antes de pasar a la siguiente fase i+1, incrementamos activeLength en 1. No hay cambios en activeNode y activeEdge. ¿Por qué? Debido a que en el caso de la regla 3, el carácter actual de la string S coincide en la misma ruta representada por el punto activo actual, por lo que para el siguiente punto activo, activeNode y activeEdge siguen siendo los mismos, solo activeLenth aumenta en 1 (debido al carácter coincidente en la fase actual ). Este nuevo ActivePoint (mismo Node, misma arista y longitud incrementada) se utilizará en la fase i+1.

   Cambio de activePoint para caminar hacia abajo (APCFWD) : activePoint puede cambiar al final de una extensión según la regla de extensión aplicada. activePoint también puede cambiar durante la extensión cuando caminamos hacia abajo. Consideremos que un punto activo es (A, s, 11) en la figura de ejemplo de punto activo anterior. Si este es el punto activo al comienzo de alguna extensión, entonces mientras camina hacia abajo desde el Node activo A, se verán otros Nodes internos. En cualquier momento, si encontramos un Node interno mientras caminamos hacia abajo, ese Node se convertirá en activeNode (cambiará activeEdge y activeLenght según corresponda para que el nuevo activePoint represente el mismo punto que antes). En este recorrido, a continuación se muestra la secuencia de cambios en activePoint:
   (A, s, 11) — >>> (B, w, 7) —- >>> (C, a, 3)
   Todos los tres activePoints anteriores se refieren a mismo punto ‘c’
   Tomemos otro ejemplo.
   Si activePoint es (D, a, 11) al comienzo de una extensión, mientras camina hacia abajo, a continuación se muestra la secuencia de cambios en activePoint:
   (D, a, 10) — >>> (E, d, 7) — >>> (F, f, 5) — >> (G, j, 1)
   Todos los puntos activos anteriores se refieren al mismo punto ‘k’.
   Si los puntos activos son (A, s, 3), (A, t, 5), (B, w, 1), (D, a, 2), etc. cuando ningún Node interno se interpone en el camino hacia abajo, entonces habrá no habrá cambios en activePoint para APCFWD.
   La idea es que, en cualquier momento, el Node interno más cercano al punto al que queremos llegar sea el ActivePoint. ¿Por qué? Esto minimizará la longitud del recorrido en la siguiente extensión.

   cambio de activePoint para Active Length ZERO (APCFALZ) : Consideremos un activePoint (A, s, 0) en la figura de ejemplo de activePoint anterior. Y digamos que el carácter actual que se procesa desde la string S es ‘x’ (o cualquier otro carácter). Al comienzo de la extensión, cuando activeLength es CERO, activeEdge se establece en el carácter actual que se está procesando, es decir, ‘x’, porque no se necesita caminar hacia abajo aquí (ya que activeLength es CERO) y, por lo tanto, el siguiente carácter que buscamos es el carácter actual siendo procesado.

4. Durante la implementación del código, recorreremos todos los caracteres de la string S uno por uno. Cada bucle para el i ^-ésimo carácter realizará el procesamiento para la fase i. El bucle se ejecutará una o más veces según la cantidad de extensiones que queden por realizar (tenga en cuenta que en una fase i+1, en realidad no tenemos que realizar todas las extensiones i+1 explícitamente, ya que el truco 3 se encargará de extensiones j para todos los bordes de las hojas j provenientes de la fase i anterior). Usaremos una variable que permaneceSuffixCount, para realizar un seguimiento de cuántas extensiones quedan por realizar explícitamente en cualquier fase (después de realizar el truco 3). Además, al final de cualquier fase, si restingSuffixCount es CERO, esto indica que todos los sufijos que se supone que deben agregarse en el árbol, se agregan explícitamente y están presentes en el árbol. Si restingSuffixCount es distinto de cero al final de cualquier fase, eso indica que los sufijos de esa cantidad no se agregan explícitamente en el árbol (debido a la regla 3, nos detuvimos temprano), pero están en el árbol implícitamente (dichos árboles se llaman árbol de sufijos implícitos). Estos sufijos implícitos se agregarán explícitamente en fases posteriores cuando un carácter único se interponga en el camino.

Continuaremos nuestra discusión en la Parte 4 y la Parte 5 . La implementación del código se discutirá en la Parte 6 .

Referencias :
http://web.stanford.edu/~mjkay/gusfield.pdf
Algoritmo de árbol de sufijos de Ukkonen en inglés simple

Este artículo es una contribución de Anurag Singh . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.