Construcción del árbol de sufijos de Ukkonen – Parte 5

Este artículo es la continuación de los siguientes cuatro artículos:
Construcción del árbol de sufijos de Ukkonen – Parte 1
Construcción del árbol de sufijos de Ukkonen – Parte 2
Construcción del árbol de sufijos de Ukkonen – Parte 3
Construcción del árbol de sufijos de Ukkonen – Parte 4

Lea la Parte 1 , la Parte 2 , la Parte 3 y la Parte 4 , antes de ver el artículo actual, donde hemos visto algunos conceptos básicos sobre el árbol de sufijos, el algoritmo de ukkonen de alto nivel, el enlace de sufijo y tres trucos de implementación y algunos detalles sobre activePoint junto con un string de ejemplo «abcabxabcd» donde pasamos por seis fases de construcción del árbol de sufijos.
Aquí, pasaremos por el resto de las fases (7 a 11) y construiremos el árbol por completo.

********************Fase 7*************************** ******
En la fase 7, leemos el séptimo ^carácter (a) de la string S

• Establezca END en 7 (esto hará las extensiones 1, 2, 3, 4, 5 y 6), porque tenemos 6 bordes de hojas hasta el final de la fase 6 anterior.

• Incremente la cuenta de sufijo restante en 1 (la cuenta de sufijo restante será 1 aquí, es decir, solo queda 1 extensión por realizar, que es la extensión 7 para el sufijo ‘a’)
• Ejecute un ciclo que resta SufijoContar veces (es decir, una vez) como se muestra a continuación:
• Si activeLength es CERO [activePoint en la fase anterior era (root, x, 0)], establezca activeEdge en el carácter actual (aquí activeEdge será ‘a’). Esto es APCFALZ . Ahora activePoint se convierte en (raíz, ‘a’, 0).
• Verifique si hay un borde que sale de activeNode (que es raíz en esta fase 7) para activeEdge. Si no, crea un borde de hoja. Si está presente, camine hacia abajo. En nuestro ejemplo, el borde ‘a’ está presente saliendo de activeNode (es decir, raíz), aquí incrementamos activeLength de cero a 1 ( APCFER3 ) y detenemos cualquier procesamiento adicional.
• En este punto, activePoint es (root, a, 1) y restingSuffixCount permanece establecido en 1 (sin cambios allí)

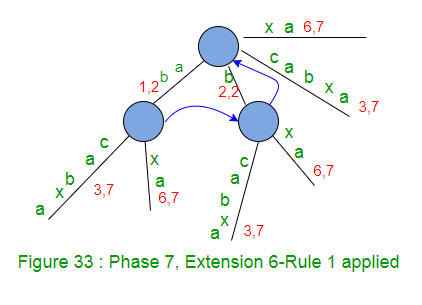
Al final de la fase 7, el número de sufijos restantes es 1 (un sufijo ‘a’, el último, no se agrega explícitamente en el árbol, pero está implícitamente en el árbol).
Arriba de la Figura 33 está el árbol resultante después de la fase 7.

********************Fase 8*************************** ******
En la fase 8, leemos el 8º ^carácter (b) de la string S

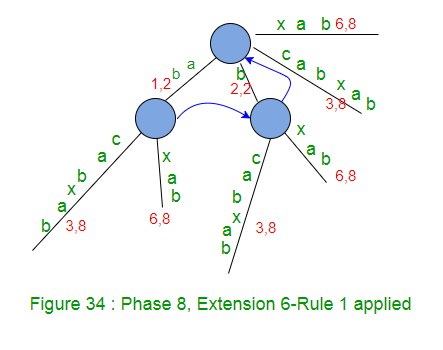
• Establezca FIN en 8 (esto hará las extensiones 1, 2, 3, 4, 5 y 6), porque hasta ahora tenemos 6 bordes de hoja al final de la fase 7 anterior (Figura 34).

• Incremente el número de sufijos restantes en 1 (el número de sufijos restantes será 2 aquí, es decir, quedan dos extensiones por realizar, que son las extensiones 7 y 8 para los sufijos ‘ab’ y ‘b’ respectivamente)
• Ejecute un ciclo que resta SufijoCuenta veces (es decir, dos veces) como se muestra a continuación:
• Verifique si hay un borde que sale de activeNode (que es raíz en esta fase 8) para activeEdge. Si no, crea un borde de hoja. Si está presente, camine hacia abajo. En nuestro ejemplo, el borde ‘a’ está presente saliendo de activeNode (es decir, raíz).
• Haga una caminata hacia abajo (El truco 1 – saltar/contar) si es necesario. En la fase 8 actual, no es necesario caminar hacia abajo ya que activeLength < edgeLength. Aquí activePoint es (root, a, 1) para la extensión 7 (remainingSuffixCount = 2)
• Compruebe si el carácter actual de la string S (que es ‘b’) ya está presente después del punto activo. En caso afirmativo, no más procesamiento (regla 3). Lo mismo ocurre en nuestro ejemplo, por lo que incrementamos activeLength de 1 a 2 ( APCFER3 ) y nos detenemos aquí (Regla 3).
• En este punto, activePoint es (raíz, a, 2) y el número de sufijos restante permanece establecido en 2 (sin cambios en el número de sufijos restantes)

Al final de la fase 8, el número de sufijos restantes es 2 (dos sufijos, ‘ab’ y ‘b’, los dos últimos, no se agregan explícitamente en el árbol, pero están en el árbol implícitamente).

********************Fase 9*************************** ******
En la fase 9, leemos el ^noveno carácter (c) de la string S

• Establezca END en 9 (esto hará las extensiones 1, 2, 3, 4, 5 y 6), porque tenemos 6 bordes de hojas hasta el final de la fase 8 anterior.

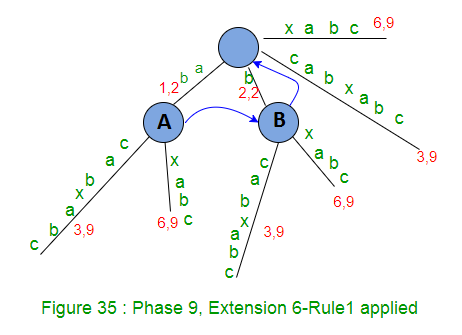
• Incremente el número de sufijos restantes en 1 (el número de sufijos restantes será 3 aquí, es decir, quedan tres extensiones por realizar, que son las extensiones 7, 8 y 9 para los sufijos ‘abc’, ‘bc’ y ‘c’ respectivamente)
• Ejecute un ciclo restante de SufijoContador veces (es decir, tres veces) como se muestra a continuación:
• Verifique si hay un borde que sale de activeNode (que es raíz en esta fase 9) para activeEdge. Si no, crea un borde de hoja. Si está presente, camine hacia abajo. En nuestro ejemplo, el borde ‘a’ está presente saliendo de activeNode (es decir, raíz).
• Haga una caminata hacia abajo (El truco 1 – saltar/contar) si es necesario. En la fase actual 9, caminar hacia abajo es necesario como activeLength(2) >= edgeLength(2). Mientras camina hacia abajo, activePoint cambia a (Node A, c, 0) según APCFWD (esta es la primera vez que se aplica APCFWD en nuestro ejemplo).
• Compruebe si el carácter actual de la string S (que es ‘c’) ya está presente después del punto activo. En caso afirmativo, no más procesamiento (regla 3). Lo mismo ocurre en nuestro ejemplo, por lo que incrementamos activeLength de 0 a 1 ( APCFER3 ) y nos detenemos aquí (Regla 3).
• En este punto, activePoint es (Node A, c, 1) y el número restante de sufijos permanece establecido en 3 (sin cambios en el número restante de sufijos)

Al final de la fase 9, el número de sufijos restantes es 3 (tres sufijos, ‘abc’, ‘bc’ y ‘c’, los últimos tres, no se agregan explícitamente en el árbol, pero sí lo están de forma implícita).

********************Fase 10*************************** ******
En la fase 10, leemos el ^décimo carácter (d) de la string S

• Establezca END en 10 (esto hará las extensiones 1, 2, 3, 4, 5 y 6), porque tenemos 6 bordes de hojas hasta el final de la fase 9 anterior.

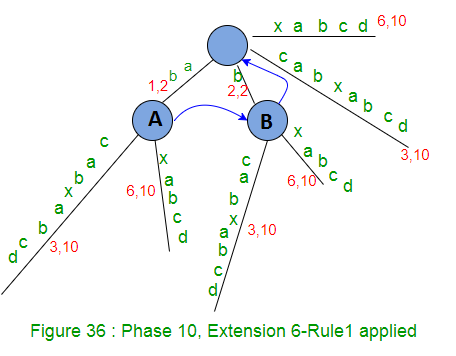
• Incremente el número de sufijos restantes en 1 (el número de sufijos restantes será 4 aquí, es decir, quedan cuatro extensiones por realizar, que son las extensiones 7, 8, 9 y 10 para los sufijos ‘abcd’, ‘bcd’, ‘cd’ y ‘d’ respectivamente)
• Ejecute un ciclo que resta SufijoCuenta veces (es decir, cuatro veces) como se muestra a continuación:
********************Extensión 7*************************** ******
• Compruebe si hay un borde que sale del Node activo (Node A) para el borde activo (c). Si no, crea un borde de hoja. Si está presente, camine hacia abajo. En nuestro ejemplo, el borde ‘c’ está presente al salir de activeNode (Node A).
• Haga una caminata hacia abajo (El truco 1 – saltar/contar) si es necesario. En la Extensión 7 actual, no es necesario caminar hacia abajo ya que activeLength < edgeLength.
• Compruebe si el carácter actual de la string S (que es ‘d’) ya está presente después del punto activo. En caso contrario, se aplicará la regla 2. En nuestro ejemplo, no hay una ruta que comience con ‘d’ que salga de activePoint, por lo que creamos un borde de hoja con la etiqueta ‘d’. Dado que activePoint termina en medio de un borde, crearemos un nuevo Node interno justo después del activePoint (Regla 2)

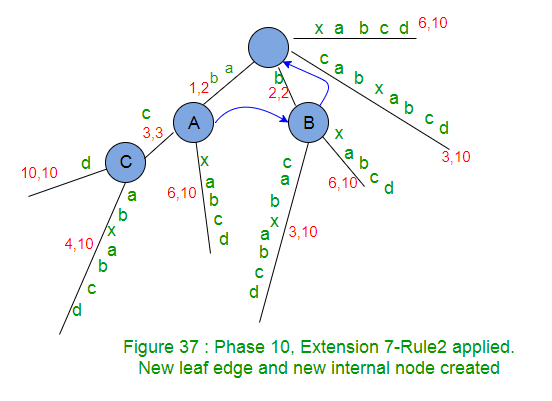
• Disminuya el RestanteSuffixCount en 1 (de 4 a 3) como sufijo «abcd» agregado en el árbol.
• Ahora activePoint cambiará para la próxima extensión 8. ActiveNode actual es un Node interno (Node A), por lo que debe haber un enlace de sufijo desde allí y lo seguiremos para obtener un nuevo activeNode y ese será ‘Node B’. No hay cambios en activeEdge y activeLength (Esto es APCFER2C2 ). Así que el nuevo punto activo es (Node B, c, 1).

********************Extensión 8*************************** ******

• Ahora, en la extensión 8 (aquí agregaremos el sufijo ‘bcd’), al agregar el carácter ‘d’ después del punto activo actual, se aplicará exactamente la misma lógica que en la extensión 7 anterior. En la extensión 7 anterior, agregamos el carácter ‘d’ en el punto activo ( Node A, c, 1) y en la extensión actual 8, vamos a agregar el mismo carácter ‘d’ en activePoint (Node B c, 1). Entonces, la lógica será la misma y aquí se creará un nuevo borde de hoja con la etiqueta ‘d’ y un nuevo Node interno. Y el nuevo Node interno (C) de la extensión anterior apuntará al nuevo Node (D) de la extensión actual a través del enlace de sufijo.

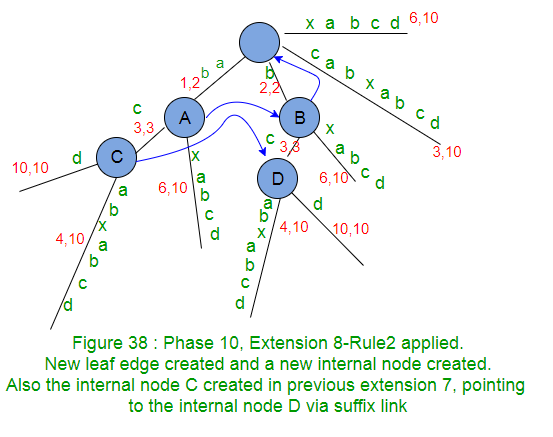
• Disminuya el resto de SuffixCount en 1 (de 3 a 2) como sufijo «bcd» agregado en el árbol.
• Ahora activePoint cambiará para la próxima extensión 9. ActiveNode actual es un Node interno (Node B), por lo que debe haber un enlace de sufijo desde allí y lo seguiremos para obtener un nuevo ActiveNode y ese es ‘Root Node’. No hay cambios en activeEdge y activeLength (Esto es APCFER2C2 ). Así que el nuevo punto activo es (raíz, c, 1).

********************Extensión 9*************************** ******

• Ahora, en la extensión 9 (aquí agregaremos el sufijo ‘cd’), al agregar el carácter ‘d’ después del ActivePoint actual, se aplicará exactamente la misma lógica que las extensiones anteriores 7 y 8. Tenga en cuenta que el Node interno D creado en la extensión 8 anterior, ahora apunta al Node interno E (creado en la extensión actual) a través del enlace de sufijo.

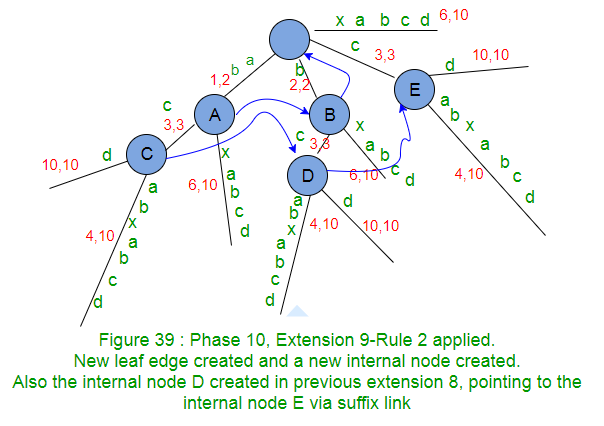
• Disminuya el resto de SuffixCount en 1 (de 2 a 1) como sufijo «cd» agregado en el árbol.
• Ahora activePoint cambiará para la próxima extensión 10. ActiveNode actual es root y activeLength es 1, según APCFER2C1 , activeNode seguirá siendo ‘root’, activeLength se reducirá en 1 (de 1 a CERO) y activeEdge será ‘d’. Así que el nuevo punto activo es (raíz, d, 0).

******************** Extensión 10*************************** ******

• Ahora, en la extensión 10 (aquí agregaremos el sufijo ‘d’), al agregar el carácter ‘d’ después del punto activo actual, no hay un borde que comience con d saliendo de la raíz del Node activo, por lo que se crea un nuevo borde de hoja con la etiqueta d ( Regla 2). Tenga en cuenta que el Node interno E creado en la extensión anterior 9, ahora apunta al Node raíz mediante un enlace de sufijo (ya que no se creó ningún Node interno nuevo en esta extensión).

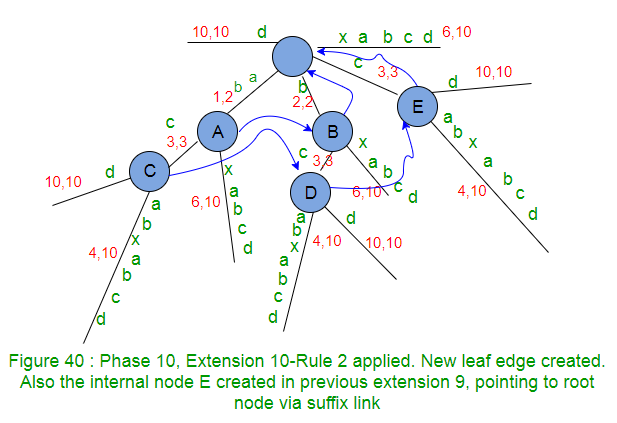
• Disminuya el RestanteSuffixCount en 1 (de 1 a 0) como sufijo «d» agregado en el árbol. Eso significa que no hay más sufijos para agregar, por lo que la fase 10 termina aquí. Tenga en cuenta que este árbol es un árbol explícito ya que todos los sufijos se agregan explícitamente en el árbol (¿Por qué? porque el carácter d no se había visto antes en la string S hasta ahora)
• activePoint para la siguiente fase 11 es (raíz, d, 0).

Vemos los siguientes hechos en la Fase 10:

• Los Nodes internos conectados a través de enlaces de sufijo tienen exactamente el mismo árbol debajo de ellos, por ejemplo, en la Figura 40 anterior, A y B tienen el mismo árbol debajo de ellos, de manera similar C, D y E tienen el mismo árbol debajo de ellos.
• Debido al hecho anterior, en cualquier extensión, cuando el Node activo actual se deriva a través del enlace de sufijo del Node activo de la extensión anterior, se aplica exactamente la misma lógica de extensión en la extensión actual que en la extensión anterior. (En la Fase 10, se aplica la misma lógica de extensión en las extensiones 7, 8 y 9)
• Si se crea un nuevo Node interno en la extensión j de cualquier fase i, entonces este Node interno recién creado obtendrá su enlace de sufijo establecido al final de la siguiente extensión j+1 de la misma fase, es decir, el Node C se creó en la extensión 7 de la fase 10 (Figura 37) y obtuvo su enlace de sufijo establecido en el Node D en la extensión 8 de la misma fase 10 (Figura 38). De manera similar, el Node D se creó en la extensión 8 de la fase 10 (Figura 38) y obtuvo su enlace de sufijo establecido en el Node E en la extensión 9 de la misma fase 10 (Figura 39). De manera similar, se creó el Node E en la extensión 9 de la fase 10 (Figura 39) y se estableció su enlace de sufijo como raíz en la extensión 10 de la misma fase 10 (Figura 40).
• Según el hecho anterior, cada Node interno tendrá un enlace de sufijo a algún otro Node interno o raíz. Root no es un Node interno y no tendrá enlace de sufijo.

********************Fase 11*************************** ******
En la fase 11, leemos el ^carácter 11 ($) de la string S

• Establezca END en 11 (esto hará las extensiones 1 a 10), porque tenemos 10 bordes de hojas hasta el final de la fase anterior 10.

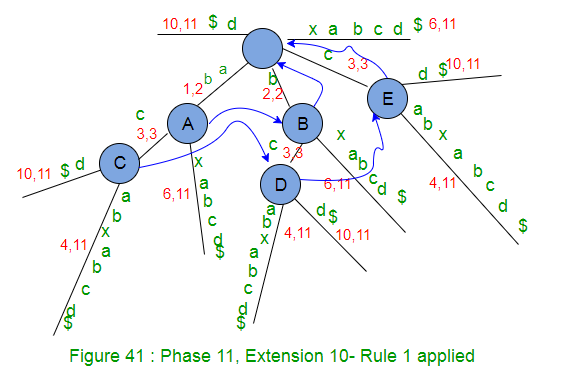
• Incremente el número de sufijos restantes en 1 (de 0 a 1), es decir, solo hay un sufijo ‘$’ para agregar en el árbol.
• Dado que activeLength es CERO, activeEdge cambiará al carácter actual ‘$’ de la string S que se está procesando ( APCFALZ ).
• No hay un borde que salga de la raíz de activeNode, por lo que se creará un borde de hoja con la etiqueta ‘$’ (Regla 2).

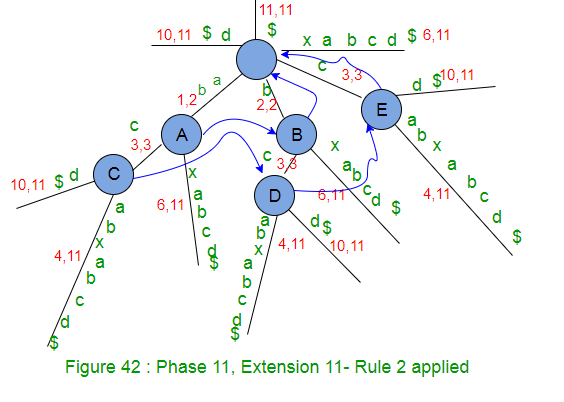
• Disminuya el RestanteSuffixCount en 1 (de 1 a 0) como sufijo «$» agregado en el árbol. Eso significa que no hay más sufijos para agregar, por lo que la fase 11 termina aquí. Tenga en cuenta que este árbol es un árbol explícito ya que todos los sufijos se agregan explícitamente en el árbol (¿Por qué? porque el carácter $no se había visto antes en la string S hasta ahora)

Ahora hemos agregado todos los sufijos de la string ‘abcabxabcd$’ en el árbol de sufijos. Hay 11 extremos de hoja en este árbol y las etiquetas en el camino desde la raíz hasta el extremo de la hoja representan un sufijo. Ahora lo único que queda es asignar un número (índice de sufijo) a cada extremo de la hoja y ese número sería la posición de inicio del sufijo en la string S. Esto se puede hacer mediante un recorrido DFS en el árbol. Durante el recorrido DFS, realice un seguimiento de la longitud de la etiqueta y, cuando se encuentre un final de hoja, establezca el índice de sufijo como «stringSize – labelSize + 1». El árbol de sufijos indexados se verá a continuación: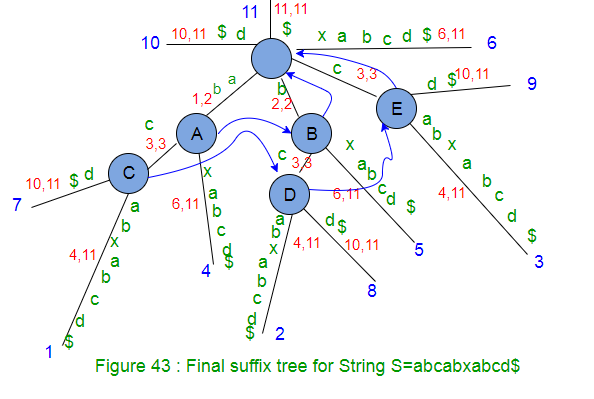

¡Y hemos terminado!

Estructura de datos para representar el árbol de sufijos
¿Cómo representar el árbol de sufijos? Hay Nodes, aristas, etiquetas y enlaces de sufijos e índices.
A continuación se muestran algunas de las operaciones/consultas que realizaremos mientras construimos el árbol de sufijos y más adelante mientras usamos el árbol de sufijos en diferentes aplicaciones/usos:

• ¿Qué longitud de etiqueta de ruta en algún borde?
• ¿Cuál es la etiqueta de ruta en algún borde?
• Compruebe si hay un borde saliente para un carácter dado desde un Node.
• ¿Cuál es el valor del carácter en un borde a cierta distancia de un Node?
• ¿Hacia dónde apunta un Node interno mediante un enlace de sufijo?
• ¿Cuál es el índice de sufijo en un camino de raíz a hoja?
• ¿Comprobar si una string determinada está presente en el árbol de sufijos (como substring, sufijo o prefijo)?

Podemos pensar en diferentes estructuras de datos que pueden cumplir con estos requisitos.
En la próxima Parte 6 , discutiremos la estructura de datos que usaremos en la implementación de nuestro código y también en el código.

Referencias :
http://web.stanford.edu/~mjkay/gusfield.pdf
Algoritmo de árbol de sufijos de Ukkonen en inglés simple

Este artículo es una contribución de Anurag Singh . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.