Consideremos los siguientes recorridos:
- Secuencia en orden: DBEAFC
- Secuencia de preorden: ABDECF
En una secuencia de pedido anticipado, el elemento más a la izquierda es la raíz del árbol. Entonces sabemos que ‘A’ es la raíz de las secuencias dadas. Al buscar ‘A’ en la secuencia Inorder, podemos encontrar que todos los elementos en el lado izquierdo de ‘A’ están en el subárbol izquierdo y los elementos a la derecha en el subárbol derecho. Ahora conocemos la siguiente estructura.
A
/ \
/ \
D B E F C
Seguimos recursivamente los pasos anteriores y obtenemos el siguiente árbol.
A
/ \
/ \
B C
/ \ /
/ \ /
D E F
Algoritmo: buildTree()
- Elija un elemento de Preorder. Incremente una variable de índice de pedido anticipado (preÍndice en el código a continuación) para elegir el siguiente elemento en la próxima llamada recursiva.
- Cree un nuevo Node de árbol tNode con los datos como elemento seleccionado.
- Encuentre el índice del elemento seleccionado en Inorder. Deje que el índice esté enIndex.
- Llame a buildTree para elementos antes de inIndex y haga que el árbol construido sea un subárbol izquierdo de tNode.
- Llame a buildTree para elementos después de inIndex y haga que el árbol construido sea un subárbol derecho de tNode.
- devolver tNode.
C++
/* C++ program to construct tree using
inorder and preorder traversals */
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node
{
public:
char data;
node* left;
node* right;
};
/* Prototypes for utility functions */
int search(char arr[], int strt, int end, char value);
node* newNode(char data);
/* Recursive function to construct binary
of size len from Inorder traversal in[]
and Preorder traversal pre[]. Initial values
of inStrt and inEnd should be 0 and len -1.
The function doesn't do any error checking
for cases where inorder and preorder do not
form a tree */
node* buildTree(char in[], char pre[], int inStrt, int inEnd)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
/* Pick current node from Preorder
traversal using preIndex
and increment preIndex */
node* tNode = newNode(pre[preIndex++]);
/* If this node has no children then return */
if (inStrt == inEnd)
return tNode;
/* Else find the index of this node in Inorder traversal */
int inIndex = search(in, inStrt, inEnd, tNode->data);
/* Using index in Inorder traversal, construct left and
right subtress */
tNode->left = buildTree(in, pre, inStrt, inIndex - 1);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
/* UTILITY FUNCTIONS */
/* Function to find index of value in arr[start...end]
The function assumes that value is present in in[] */
int search(char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++)
{
if (arr[i] == value)
return i;
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(char data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
/* This function is here just to test buildTree() */
void printInorder(node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout<<node->data<<" ";
/* now recur on right child */
printInorder(node->right);
}
/* Driver code */
int main()
{
char in[] = { 'D', 'B', 'E', 'A', 'F', 'C' };
char pre[] = { 'A', 'B', 'D', 'E', 'C', 'F' };
int len = sizeof(in) / sizeof(in[0]);
node* root = buildTree(in, pre, 0, len - 1);
/* Let us test the built tree by
printing Inorder traversal */
cout << "Inorder traversal of the constructed tree is \n";
printInorder(root);
}
// This is code is contributed by rathbhupendra
C
/* program to construct tree using inorder and preorder traversals */
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
char data;
struct node* left;
struct node* right;
};
/* Prototypes for utility functions */
int search(char arr[], int strt, int end, char value);
struct node* newNode(char data);
/* Recursive function to construct binary of size len from
Inorder traversal in[] and Preorder traversal pre[]. Initial values
of inStrt and inEnd should be 0 and len -1. The function doesn't
do any error checking for cases where inorder and preorder
do not form a tree */
struct node* buildTree(char in[], char pre[], int inStrt, int inEnd)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
struct node* tNode = newNode(pre[preIndex++]);
/* If this node has no children then return */
if (inStrt == inEnd)
return tNode;
/* Else find the index of this node in Inorder traversal */
int inIndex = search(in, inStrt, inEnd, tNode->data);
/* Using index in Inorder traversal, construct left and
right subtress */
tNode->left = buildTree(in, pre, inStrt, inIndex - 1);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
/* UTILITY FUNCTIONS */
/* Function to find index of value in arr[start...end]
The function assumes that value is present in in[] */
int search(char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value)
return i;
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(char data)
{
struct node* node = (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* This function is here just to test buildTree() */
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%c ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Driver program to test above functions */
int main()
{
char in[] = { 'D', 'B', 'E', 'A', 'F', 'C' };
char pre[] = { 'A', 'B', 'D', 'E', 'C', 'F' };
int len = sizeof(in) / sizeof(in[0]);
struct node* root = buildTree(in, pre, 0, len - 1);
/* Let us test the built tree by printing Inorder traversal */
printf("Inorder traversal of the constructed tree is \n");
printInorder(root);
getchar();
}
Java
// Java program to construct a tree using inorder and preorder traversal
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class Node {
char data;
Node left, right;
Node(char item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
static int preIndex = 0;
/* Recursive function to construct binary of size len from
Inorder traversal in[] and Preorder traversal pre[].
Initial values of inStrt and inEnd should be 0 and len -1.
The function doesn't do any error checking for cases where
inorder and preorder do not form a tree */
Node buildTree(char in[], char pre[], int inStrt, int inEnd)
{
if (inStrt > inEnd)
return null;
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
Node tNode = new Node(pre[preIndex++]);
/* If this node has no children then return */
if (inStrt == inEnd)
return tNode;
/* Else find the index of this node in Inorder traversal */
int inIndex = search(in, inStrt, inEnd, tNode.data);
/* Using index in Inorder traversal, construct left and
right subtress */
tNode.left = buildTree(in, pre, inStrt, inIndex - 1);
tNode.right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
/* UTILITY FUNCTIONS */
/* Function to find index of value in arr[start...end]
The function assumes that value is present in in[] */
int search(char arr[], int strt, int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value)
return i;
}
return i;
}
/* This function is here just to test buildTree() */
void printInorder(Node node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
System.out.print(node.data + " ");
/* now recur on right child */
printInorder(node.right);
}
// driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
char in[] = new char[] { 'D', 'B', 'E', 'A', 'F', 'C' };
char pre[] = new char[] { 'A', 'B', 'D', 'E', 'C', 'F' };
int len = in.length;
Node root = tree.buildTree(in, pre, 0, len - 1);
// building the tree by printing inorder traversal
System.out.println("Inorder traversal of constructed tree is : ");
tree.printInorder(root);
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# Python program to construct tree using inorder and
# preorder traversals
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
"""Recursive function to construct binary of size len from
Inorder traversal in[] and Preorder traversal pre[]. Initial values
of inStrt and inEnd should be 0 and len -1. The function doesn't
do any error checking for cases where inorder and preorder
do not form a tree """
def buildTree(inOrder, preOrder, inStrt, inEnd):
if (inStrt > inEnd):
return None
# Pick current node from Preorder traversal using
# preIndex and increment preIndex
tNode = Node(preOrder[buildTree.preIndex])
buildTree.preIndex += 1
# If this node has no children then return
if inStrt == inEnd :
return tNode
# Else find the index of this node in Inorder traversal
inIndex = search(inOrder, inStrt, inEnd, tNode.data)
# Using index in Inorder Traversal, construct left
# and right subtrees
tNode.left = buildTree(inOrder, preOrder, inStrt, inIndex-1)
tNode.right = buildTree(inOrder, preOrder, inIndex + 1, inEnd)
return tNode
# UTILITY FUNCTIONS
# Function to find index of value in arr[start...end]
# The function assumes that value is present in inOrder[]
def search(arr, start, end, value):
for i in range(start, end + 1):
if arr[i] == value:
return i
def printInorder(node):
if node is None:
return
# first recur on left child
printInorder(node.left)
# then print the data of node
print (node.data,end=' ')
# now recur on right child
printInorder(node.right)
# Driver program to test above function
inOrder = ['D', 'B', 'E', 'A', 'F', 'C']
preOrder = ['A', 'B', 'D', 'E', 'C', 'F']
# Static variable preIndex
buildTree.preIndex = 0
root = buildTree(inOrder, preOrder, 0, len(inOrder)-1)
# Let us test the build tree by printing Inorder traversal
print ("Inorder traversal of the constructed tree is")
printInorder(root)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// C# program to construct a tree using
// inorder and preorder traversal
using System;
/* A binary tree node has data, pointer
to left child and a pointer to right child */
public class Node {
public char data;
public Node left, right;
public Node(char item)
{
data = item;
left = right = null;
}
}
class GFG {
public Node root;
public static int preIndex = 0;
/* Recursive function to construct binary
of size len from Inorder traversal in[]
and Preorder traversal pre[]. Initial values
of inStrt and inEnd should be 0 and len -1.
The function doesn't do any error checking for
cases where inorder and preorder do not form a tree */
public virtual Node buildTree(char[] arr, char[] pre,
int inStrt, int inEnd)
{
if (inStrt > inEnd) {
return null;
}
/* Pick current node from Preorder traversal
using preIndex and increment preIndex */
Node tNode = new Node(pre[preIndex++]);
/* If this node has no children then return */
if (inStrt == inEnd) {
return tNode;
}
/* Else find the index of this
node in Inorder traversal */
int inIndex = search(arr, inStrt,
inEnd, tNode.data);
/* Using index in Inorder traversal,
construct left and right subtress */
tNode.left = buildTree(arr, pre, inStrt, inIndex - 1);
tNode.right = buildTree(arr, pre, inIndex + 1, inEnd);
return tNode;
}
/* UTILITY FUNCTIONS */
/* Function to find index of value in arr[start...end]
The function assumes that value is present in in[] */
public virtual int search(char[] arr, int strt,
int end, char value)
{
int i;
for (i = strt; i <= end; i++) {
if (arr[i] == value) {
return i;
}
}
return i;
}
/* This function is here just to test buildTree() */
public virtual void printInorder(Node node)
{
if (node == null) {
return;
}
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
Console.Write(node.data + " ");
/* now recur on right child */
printInorder(node.right);
}
// Driver Code
public static void Main(string[] args)
{
GFG tree = new GFG();
char[] arr = new char[] { 'D', 'B', 'E', 'A', 'F', 'C' };
char[] pre = new char[] { 'A', 'B', 'D', 'E', 'C', 'F' };
int len = arr.Length;
Node root = tree.buildTree(arr, pre, 0, len - 1);
// building the tree by printing inorder traversal
Console.WriteLine("Inorder traversal of "
+ "constructed tree is : ");
tree.printInorder(root);
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// Javascript program to construct a
// tree using inorder and preorder traversal
// A binary tree node has data, pointer
// to left child and a pointer to right child
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right = null;
}
}
let root;
let preIndex = 0;
// Recursive function to construct binary
// of size len from Inorder traversal in[]
// and Preorder traversal pre[]. Initial
// values of inStrt and inEnd should be 0
// and len -1. The function doesn't do any
// error checking for cases where inorder
// and preorder do not form a tree
function buildTree(In, pre, inStrt, inEnd)
{
if (inStrt > inEnd)
return null;
// Pick current node from Preorder
// traversal using preIndex and
// increment preIndex
let tNode = new Node(pre[preIndex++]);
// If this node has no children then return
if (inStrt == inEnd)
return tNode;
// Else find the index of this
// node in Inorder traversal
let inIndex = search(In, inStrt,
inEnd, tNode.data);
// Using index in Inorder traversal,
// construct left and right subtress
tNode.left = buildTree(In, pre, inStrt,
inIndex - 1);
tNode.right = buildTree(In, pre,
inIndex + 1,
inEnd);
return tNode;
}
/* UTILITY FUNCTIONS */
// Function to find index of value
// in arr[start...end]. The function
// assumes that value is present in in[]
function search(arr, strt, end, value)
{
let i;
for(i = strt; i <= end; i++)
{
if (arr[i] == value)
return i;
}
return i;
}
// This function is here just
// to test buildTree()
function printInorder(node)
{
if (node == null)
return;
// First recur on left child
printInorder(node.left);
// Then print the data of node
document.write(node.data + " ");
// Now recur on right child
printInorder(node.right);
}
// Driver code
let In = [ 'D', 'B', 'E', 'A', 'F', 'C' ];
let pre = [ 'A', 'B', 'D', 'E', 'C', 'F'];
let len = In.length;
root = buildTree(In, pre, 0, len - 1);
// Building the tree by printing
// inorder traversal
document.write("Inorder traversal of " +
"constructed tree is : <br>");
printInorder(root);
// This code is contributed by patel2127
</script>
Inorder traversal of the constructed tree is D B E A F C
Complejidad de tiempo: O(n^2) . El peor caso ocurre cuando el árbol está sesgado a la izquierda. Ejemplos de recorridos en orden previo y en orden para el peor de los casos son {A, B, C, D} y {D, C, B, A}.
Enfoque eficiente:
Podemos optimizar la solución anterior usando hashing (unordered_map en C++ o HashMap en Java). Almacenamos índices de recorrido en orden en una tabla hash. Entonces esa búsqueda se puede hacer O (1) tiempo.
C++
/* C++ program to construct tree using inorder
and preorder traversals */
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node {
char data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(char data)
{
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
/* Recursive function to construct binary of size
len from Inorder traversal in[] and Preorder traversal
pre[]. Initial values of inStrt and inEnd should be
0 and len -1. The function doesn't do any error
checking for cases where inorder and preorder
do not form a tree */
struct Node* buildTree(char in[], char pre[], int inStrt,
int inEnd, unordered_map<char, int>& mp)
{
static int preIndex = 0;
if (inStrt > inEnd)
return NULL;
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
char curr = pre[preIndex++];
struct Node* tNode = newNode(curr);
/* If this node has no children then return */
if (inStrt == inEnd)
return tNode;
/* Else find the index of this node in Inorder traversal */
int inIndex = mp[curr];
/* Using index in Inorder traversal, construct left and
right subtress */
tNode->left = buildTree(in, pre, inStrt, inIndex - 1, mp);
tNode->right = buildTree(in, pre, inIndex + 1, inEnd, mp);
return tNode;
}
// This function mainly creates an unordered_map, then
// calls buildTree()
struct Node* buldTreeWrap(char in[], char pre[], int len)
{
// Store indexes of all items so that we
// we can quickly find later
unordered_map<char, int> mp;
for (int i = 0; i < len; i++)
mp[in[i]] = i;
return buildTree(in, pre, 0, len - 1, mp);
}
/* This function is here just to test buildTree() */
void printInorder(struct Node* node)
{
if (node == NULL)
return;
printInorder(node->left);
printf("%c ", node->data);
printInorder(node->right);
}
/* Driver program to test above functions */
int main()
{
char in[] = { 'D', 'B', 'E', 'A', 'F', 'C' };
char pre[] = { 'A', 'B', 'D', 'E', 'C', 'F' };
int len = sizeof(in) / sizeof(in[0]);
struct Node* root = buldTreeWrap(in, pre, len);
/* Let us test the built tree by printing
Inorder traversal */
printf("Inorder traversal of the constructed tree is \n");
printInorder(root);
}
Java
/* Java program to construct tree using inorder
and preorder traversals */
import java.io.*;
import java.util.*;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class Node
{
char data;
Node left,right;
Node(char item)
{
data = item;
left = right = null;
}
}
class Tree
{
public static Node root;
// Store indexes of all items so that we
// we can quickly find later
static HashMap<Character,Integer> mp = new HashMap<>();
static int preIndex = 0;
/* Recursive function to construct binary of size
len from Inorder traversal in[] and Preorder traversal
pre[]. Initial values of inStrt and inEnd should be
0 and len -1. The function doesn't do any error
checking for cases where inorder and preorder
do not form a tree */
public static Node buildTree(char[] in, char[] pre, int inStrt, int inEnd)
{
if(inStrt > inEnd)
{
return null;
}
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
char curr = pre[preIndex++];
Node tNode;
tNode = new Node(curr);
/* If this node has no children then return */
if (inStrt == inEnd)
{
return tNode;
}
/* Else find the index of this node in Inorder traversal */
int inIndex = mp.get(curr);
/* Using index in Inorder traversal, construct left and
right subtress */
tNode.left = buildTree(in, pre, inStrt, inIndex - 1);
tNode.right = buildTree(in, pre, inIndex + 1, inEnd);
return tNode;
}
// This function mainly creates an unordered_map, then
// calls buildTree()
public static Node buldTreeWrap(char[] in, char[] pre, int len)
{
for(int i = 0; i < len; i++)
{
mp.put(in[i], i);
}
return buildTree(in, pre, 0, len - 1);
}
/* This function is here just to test buildTree() */
static void printInorder(Node node)
{
if(node == null)
{
return;
}
printInorder(node.left);
System.out.print(node.data + " ");
printInorder(node.right);
}
/* Driver code */
public static void main (String[] args)
{
char[] in = {'D', 'B', 'E', 'A', 'F', 'C'};
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F'};
int len = in.length;
Tree.root=buldTreeWrap(in, pre, len);
/* Let us test the built tree by printing
Inorder traversal */
System.out.println("Inorder traversal of the constructed tree is");
printInorder(root);
}
}
// This code is contributed by avanitrachhadiya2155
Python3
# Python3 program to construct tree using inorder
# and preorder traversals
# A binary tree node has data, pointer to left child
# and a pointer to right child
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Recursive function to construct binary of size
# len from Inorder traversal in[] and Preorder traversal
# pre[]. Initial values of inStrt and inEnd should be
# 0 and len -1. The function doesn't do any error
# checking for cases where inorder and preorder
# do not form a tree
def buildTree(inn, pre, inStrt, inEnd):
global preIndex, mp
if (inStrt > inEnd):
return None
# Pick current node from Preorder traversal
# using preIndex and increment preIndex
curr = pre[preIndex]
preIndex += 1
tNode = Node(curr)
# If this node has no children then return
if (inStrt == inEnd):
return tNode
# Else find the index of this
# node in Inorder traversal
inIndex = mp[curr]
# Using index in Inorder traversal,
# construct left and right subtress
tNode.left = buildTree(inn, pre, inStrt,
inIndex - 1)
tNode.right = buildTree(inn, pre, inIndex + 1,
inEnd)
return tNode
# This function mainly creates an
# unordered_map, then calls buildTree()
def buldTreeWrap(inn, pre, lenn):
global mp
# Store indexes of all items so that we
# we can quickly find later
# unordered_map<char, int> mp;
for i in range(lenn):
mp[inn[i]] = i
return buildTree(inn, pre, 0, lenn - 1)
# This function is here just to test buildTree()
def printInorder(node):
if (node == None):
return
printInorder(node.left)
print(node.data, end = " ")
printInorder(node.right)
# Driver code
if __name__ == '__main__':
mp = {}
preIndex = 0
inn = [ 'D', 'B', 'E', 'A', 'F', 'C' ]
pre = [ 'A', 'B', 'D', 'E', 'C', 'F' ]
lenn = len(inn)
root = buldTreeWrap(inn, pre,lenn)
# Let us test the built tree by printing
# Inorder traversal
print("Inorder traversal of "
"the constructed tree is")
printInorder(root)
# This code is contributed by mohit kumar 29
C#
/* C# program to construct tree using inorder
and preorder traversals */
using System;
using System.Collections.Generic;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
public class Node
{
public char data;
public Node left, right;
public Node(char d)
{
data = d;
left = right = null;
}
}
public class Tree
{
public static Node root;
// Store indexes of all items so that we
// we can quickly find later
static Dictionary<char,int> mp = new Dictionary<char,int>();
static int preIndex = 0;
/* Recursive function to construct binary of size
len from Inorder traversal in[] and Preorder traversal
pre[]. Initial values of inStrt and inEnd should be
0 and len -1. The function doesn't do any error
checking for cases where inorder and preorder
do not form a tree */
static Node buildTree(char[] In, char[] pre,
int inStrt, int inEnd)
{
if(inStrt > inEnd)
{
return null;
}
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
char curr = pre[preIndex++];
Node tNode;
tNode = new Node(curr);
/* If this node has no children then return */
if(inStrt == inEnd)
{
return tNode;
}
/* Else find the index of this node in Inorder traversal */
int inIndex = mp[curr];
/* Using index in Inorder traversal, construct left and
right subtress */
tNode.left = buildTree(In, pre, inStrt, inIndex - 1);
tNode.right = buildTree(In, pre, inIndex + 1, inEnd);
return tNode;
}
// This function mainly creates an unordered_map, then
// calls buildTree()
public static Node buldTreeWrap(char[] In, char[] pre, int len)
{
for(int i = 0; i < len; i++)
{
mp.Add(In[i], i);
}
return buildTree(In, pre, 0, len - 1);
}
/* This function is here just to test buildTree() */
static void printInorder(Node node)
{
if(node == null)
{
return;
}
printInorder(node.left);
Console.Write(node.data + " ");
printInorder(node.right);
}
/* Driver code */
static public void Main (){
char[] In = {'D', 'B', 'E', 'A', 'F', 'C'};
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F'};
int len = In.Length;
Tree.root = buldTreeWrap(In, pre, len);
/* Let us test the built tree by printing
Inorder traversal */
Console.WriteLine("Inorder traversal of the constructed tree is");
printInorder(Tree.root);
}
}
// This code is contributed by rag2127
Javascript
<script>
/* Javascript program to construct tree using inorder
and preorder traversals */
/* A binary tree node has data, pointer
to left child and a pointer to right child */
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right = null;
}
}
let root;
let preIndex = 0;
/* Recursive function to construct binary of size
len from Inorder traversal in[] and Preorder traversal
pre[]. Initial values of inStrt and inEnd should be
0 and len -1. The function doesn't do any error
checking for cases where inorder and preorder
do not form a tree */
function buildTree(In, pre, inStrt, inEnd, mp)
{
if (inStrt > inEnd)
return null;
/* Pick current node from Preorder traversal using preIndex
and increment preIndex */
const tNode = new Node(pre[preIndex++]);
// If this node has no children then return
if (inStrt === inEnd)
return tNode;
// Else find the index of this node in Inorder traversal
let inIndex = mp.get(tNode.data);
/* Using index in Inorder traversal, construct left and
right subtress */
tNode.left = buildTree(In, pre, inStrt, inIndex - 1);
tNode.right = buildTree(In, pre, inIndex + 1, inEnd);
return tNode;
}
/* This function mainly creates an unordered_map, then
calls buildTree() */
function buildTreeWrap(In, pre, start, end) {
const mp = new Map();
for (let i = 0; i < In.length; i++) {
mp.set(In[i], i);
}
return buildTree(In, pre, start, end, mp);
}
// This function is here just to test buildTree()
function printInorder(node)
{
if (node == null)
return;
// First recur on left child
printInorder(node.left);
// Then print the data of node
document.write(node.data + " ");
// Now recur on right child
printInorder(node.right);
}
// Driver code
let In = [ 'D', 'B', 'E', 'A', 'F', 'C' ];
let pre = [ 'A', 'B', 'D', 'E', 'C', 'F'];
let len = In.length;
root = buildTreeWrap(In, pre, 0, len - 1);
/* Let us test the built tree by printing
Inorder traversal */
document.write("Inorder traversal of constructed tree is : <br>");
printInorder(root);
// This code is contributed by thakurballary
</script>
Inorder traversal of the constructed tree is D B E A F C
Complejidad de tiempo: O(n)
Otro enfoque :
Utilice el hecho de que el recorrido InOrder es Izquierda-Raíz-Derecha y el recorrido PreOrder es Raíz-Izquierda-Derecha. Además, el primer Node del recorrido PreOrder siempre es el Node raíz y el primer Node del recorrido InOrder es el Node más a la izquierda del árbol.
Mantenga dos estructuras de datos: Stack (para almacenar la ruta que visitamos mientras atravesábamos la array PreOrder) y Set (para mantener el Node en el que se espera el siguiente subárbol derecho).
1. Haz lo siguiente hasta llegar al Node más a la izquierda.
Continúe creando los Nodes desde el recorrido PreOrder
Si el elemento superior de la pila no está en el conjunto, vincule el Node creado al elemento secundario izquierdo del elemento superior de la pila (si lo hay), sin extraer el elemento.
De lo contrario, vincule el Node creado al elemento secundario derecho del elemento superior de la pila. Retire el elemento superior de la pila del conjunto y la pila.
Empuje el Node a una pila.

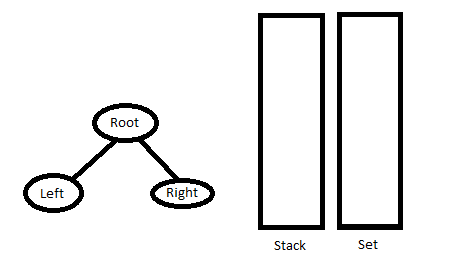
2. Siga extrayendo los Nodes de la pila hasta que la pila esté vacía o hasta que el elemento superior de la pila se compare con el elemento actual del recorrido InOrder. Una vez que finaliza el ciclo, empuje el último Node de vuelta a la pila y al conjunto.
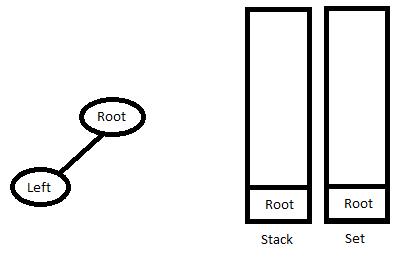
3. Vaya al Paso 1.
C++
// C++ program to construct a tree using
// inorder and preorder traversal
#include<bits/stdc++.h>
using namespace std;
class TreeNode
{
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) { val = x; }
};
set<TreeNode*> s;
stack<TreeNode*> st;
// Function to build tree using given traversal
TreeNode* buildTree(int preorder[], int inorder[],int n)
{
TreeNode* root = NULL;
for (int pre = 0, in = 0; pre < n;)
{
TreeNode* node = NULL;
do
{
node = new TreeNode(preorder[pre]);
if (root == NULL)
{
root = node;
}
if (st.size() > 0)
{
if (s.find(st.top()) != s.end())
{
s.erase(st.top());
st.top()->right = node;
st.pop();
}
else
{
st.top()->left = node;
}
}
st.push(node);
} while (preorder[pre++] != inorder[in] && pre < n);
node = NULL;
while (st.size() > 0 && in < n &&
st.top()->val == inorder[in])
{
node = st.top();
st.pop();
in++;
}
if (node != NULL)
{
s.insert(node);
st.push(node);
}
}
return root;
}
// Function to print tree in Inorder
void printInorder(TreeNode* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout << node->val << " ";
/* now recur on right child */
printInorder(node->right);
}
// Driver code
int main()
{
int in[] = { 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 };
int pre[] = { 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 };
int len = sizeof(in)/sizeof(int);
TreeNode *root = buildTree(pre, in, len);
printInorder(root);
return 0;
}
// This code is contributed by Arnab Kundu
Java
// Java program to construct a tree using inorder and preorder traversal
import java.util.*;
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class BinaryTree {
static Set<TreeNode> set = new HashSet<>();
static Stack<TreeNode> stack = new Stack<>();
// Function to build tree using given traversal
public TreeNode buildTree(int[] preorder, int[] inorder)
{
TreeNode root = null;
for (int pre = 0, in = 0; pre < preorder.length;) {
TreeNode node = null;
do {
node = new TreeNode(preorder[pre]);
if (root == null) {
root = node;
}
if (!stack.isEmpty()) {
if (set.contains(stack.peek())) {
set.remove(stack.peek());
stack.pop().right = node;
}
else {
stack.peek().left = node;
}
}
stack.push(node);
} while (preorder[pre++] != inorder[in] && pre < preorder.length);
node = null;
while (!stack.isEmpty() && in < inorder.length &&
stack.peek().val == inorder[in]) {
node = stack.pop();
in++;
}
if (node != null) {
set.add(node);
stack.push(node);
}
}
return root;
}
// Function to print tree in Inorder
void printInorder(TreeNode node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
System.out.print(node.val + " ");
/* now recur on right child */
printInorder(node.right);
}
// driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
int in[] = new int[] { 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 };
int pre[] = new int[] { 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 };
int len = in.length;
TreeNode root = tree.buildTree(pre, in);
tree.printInorder(root);
}
}
Python3
# Python3 program to construct a tree using # inorder and preorder traversal class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None s = set() st = [] # Function to build tree using given traversal def buildTree(preorder, inorder, n): root = None; pre = 0 in_t = 0 while pre < n: node = None; while True: node = TreeNode(preorder[pre]) if (root == None): root = node; if (len(st) > 0): if (st[-1] in s): s.discard(st[-1]); st[-1].right = node; st.pop(); else: st[-1].left = node; st.append(node); if pre>=n or preorder[pre] == inorder[in_t]: pre += 1 break pre += 1 node = None; while (len(st) > 0 and in_t < n and st[-1].val == inorder[in_t]): node = st[-1]; st.pop(); in_t += 1 if (node != None): s.add(node); st.append(node); return root; # Function to print tree in_t Inorder def printInorder( node): if (node == None): return; ''' first recur on left child ''' printInorder(node.left); ''' then print data of node ''' print(node.val, end=" "); ''' now recur on right child ''' printInorder(node.right); # Driver code if __name__=='__main__': in_t = [ 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 ] pre = [ 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 ] l = len(in_t) root = buildTree(pre, in_t, l); printInorder(root); # This code is contributed by rutvik_56.
C#
// C# program to construct a tree
// using inorder and preorder traversal
using System;
using System.Collections.Generic;
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) { val = x; }
}
class GFG
{
static HashSet<TreeNode> set = new HashSet<TreeNode>();
static Stack<TreeNode> stack = new Stack<TreeNode>();
// Function to build tree using given traversal
public TreeNode buildTree(int[] preorder, int[] inorder)
{
TreeNode root = null;
for (int pre = 0, iN = 0; pre < preorder.Length;)
{
TreeNode node = null;
do {
node = new TreeNode(preorder[pre]);
if (root == null)
{
root = node;
}
if (stack.Count != 0)
{
if (set.Contains(stack.Peek()))
{
set.Remove(stack.Peek());
stack.Pop().right = node;
}
else
{
stack.Peek().left = node;
}
}
stack.Push(node);
} while (preorder[pre++] != inorder[iN] &&
pre < preorder.Length);
node = null;
while (stack.Count != 0 && iN < inorder.Length &&
stack.Peek().val == inorder[iN])
{
node = stack.Pop();
iN++;
}
if (node != null)
{
set.Add(node);
stack.Push(node);
}
}
return root;
}
// Function to print tree in Inorder
void printInorder(TreeNode node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
Console.Write(node.val + " ");
/* now recur on right child */
printInorder(node.right);
}
// Driver Code
public static void Main(String []args)
{
GFG tree = new GFG();
int []iN = new int[] { 9, 8, 4, 2, 10, 5, 10,
1, 6, 3, 13, 12, 7 };
int []pre = new int[] { 1, 2, 4, 8, 9, 5, 10,
10, 3, 6, 7, 12, 13 };
int len = iN.Length;
TreeNode root = tree.buildTree(pre, iN);
tree.printInorder(root);
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to construct a tree using inorder and preorder traversal
class TreeNode
{
constructor(x) {
this.val = x;
this.left = null;
this.right = null;
}
}
let set = new Set();
let stack = [];
// Function to build tree using given traversal
function buildTree(preorder,inorder)
{
let root = null;
for (let pre = 0,In=0; pre < preorder.length;) {
let node = null;
do {
node = new TreeNode(preorder[pre]);
if (root == null) {
root = node;
}
if (stack.length!=0) {
if (set.has(stack[stack.length-1])) {
set.delete(stack[stack.length-1]);
stack.pop().right = node;
}
else {
stack[stack.length-1].left = node;
}
}
stack.push(node);
} while (preorder[pre++] != inorder[In] && pre < preorder.length);
node = null;
while (stack.length!=0 && In < inorder.length &&
stack[stack.length-1].val == inorder[In]) {
node = stack.pop();
In++;
}
if (node != null) {
set.add(node);
stack.push(node);
}
}
return root;
}
// Function to print tree in Inorder
function printInorder(node)
{
if (node == null)
return;
/* first recur on left child */
printInorder(node.left);
/* then print the data of node */
document.write(node.val + " ");
/* now recur on right child */
printInorder(node.right);
}
// driver program to test above functions
let In=[9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 ];
let pre=[1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 ];
let len = In.length;
let root=buildTree(pre, In);
printInorder(root);
// This code is contributed by unknown2108
</script>
9 8 4 2 10 5 10 1 6 3 13 12 7
Construya un árbol binario a partir de Postorder y Inorder
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA