Dados los recorridos en orden y en orden de nivel de un árbol binario, construya el árbol binario. A continuación se muestra un ejemplo para ilustrar el problema.
Input: Two arrays that represent Inorder
and level order traversals of a
Binary Tree
in[] = {4, 8, 10, 12, 14, 20, 22};
level[] = {20, 8, 22, 4, 12, 10, 14};
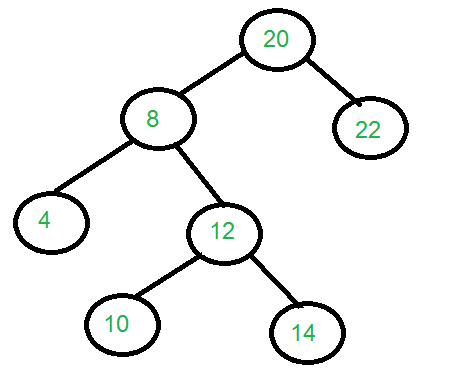
Output: Construct the tree represented
by the two arrays.
For the above two arrays, the
constructed tree is shown in
the diagram on right side
La siguiente publicación puede considerarse como un requisito previo para esto.
Construir un árbol a partir de recorridos en orden y en orden previo dados
Consideremos el ejemplo anterior.
- en[] = {4, 8, 10, 12, 14, 20, 22};
- nivel[] = {20, 8, 22, 4, 12, 10, 14};
En una secuencia de Levelorder, el primer elemento es la raíz del árbol. Entonces sabemos que ’20’ es raíz para secuencias dadas. Al buscar ’20’ en secuencia Inorder, podemos encontrar que todos los elementos del lado izquierdo de ’20’ están en el subárbol izquierdo y los elementos de la derecha están en el subárbol derecho. Entonces sabemos la estructura debajo ahora.
20
/ \
/ \
{4,8,10,12,14} {22}
Llamemos {4,8,10,12,14} como subarreglo izquierdo en el recorrido Inorder y {22} como subarreglo derecho en el recorrido Inorder.
En el recorrido por orden de niveles, las claves de los subárboles izquierdo y derecho no son consecutivas. Entonces extraemos todos los Nodes del recorrido de orden de nivel que están en el subarreglo izquierdo del recorrido de Inorder. Para construir el subárbol izquierdo de la raíz, recurrimos a los elementos extraídos del recorrido de orden de nivel y el subarreglo izquierdo del recorrido de orden. En el ejemplo anterior, recurrimos a las siguientes dos arrays.
// Recur for following arrays to construct the left subtree
In[] = {4, 8, 10, 12, 14}
level[] = {8, 4, 12, 10, 14}
De manera similar, recurrimos a los siguientes dos arreglos y construimos el subárbol derecho.
// Recur for following arrays to construct the right subtree
In[] = {22}
level[] = {22}
La siguiente es la implementación del enfoque anterior:
C++
/* program to construct tree using inorder and levelorder
* traversals */
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node */
struct Node {
int key;
struct Node *left, *right;
};
/* Function to find index of value in arr[start...end] */
int search(int arr[], int strt, int end, int value)
{
for (int i = strt; i <= end; i++)
if (arr[i] == value)
return i;
return -1;
}
// n is size of level[], m is size of in[] and m < n. This
// function extracts keys from level[] which are present in
// in[]. The order of extracted keys must be maintained
int* extrackKeys(int in[], int level[], int m, int n)
{
int *newlevel = new int[m], j = 0;
for (int i = 0; i < n; i++)
if (search(in, 0, m - 1, level[i]) != -1)
newlevel[j] = level[i], j++;
return newlevel;
}
/* function that allocates a new node with the given key */
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return (node);
}
/* Recursive function to construct binary tree of size n
from Inorder traversal in[] and Level Order traversal
level[]. inStrt and inEnd are start and end indexes of
array in[] Initial values of inStrt and inEnd should be 0
and n -1. The function doesn't do any error checking for
cases where inorder and levelorder do not form a tree */
Node* buildTree(int in[], int level[], int inStrt,
int inEnd, int n)
{
// If start index is more than the end index
if (inStrt > inEnd)
return NULL;
/* The first node in level order traversal is root */
Node* root = newNode(level[0]);
/* If this node has no children then return */
if (inStrt == inEnd)
return root;
/* Else find the index of this node in Inorder traversal
*/
int inIndex = search(in, inStrt, inEnd, root->key);
// Extract left subtree keys from level order traversal
int* llevel = extrackKeys(in, level, inIndex, n);
// Extract right subtree keys from level order traversal
int* rlevel
= extrackKeys(in + inIndex + 1, level, n - 1, n);
/* construct left and right subtrees */
root->left = buildTree(in, llevel, inStrt, inIndex - 1,
inIndex - inStrt);
root->right = buildTree(in, rlevel, inIndex + 1, inEnd,
inEnd - inIndex);
// Free memory to avoid memory leak
delete[] llevel;
delete[] rlevel;
return root;
}
/* utility function to print inorder traversal of binary
* tree */
void printInorder(Node* node)
{
if (node == NULL)
return;
printInorder(node->left);
cout << node->key << " ";
printInorder(node->right);
}
/* Driver program to test above functions */
int main()
{
int in[] = { 4, 8, 10, 12, 14, 20, 22 };
int level[] = { 20, 8, 22, 4, 12, 10, 14 };
int n = sizeof(in) / sizeof(in[0]);
Node* root = buildTree(in, level, 0, n - 1, n);
/* Let us test the built tree by printing Inorder
* traversal */
cout << "Inorder traversal of the constructed tree is "
"\n";
printInorder(root);
return 0;
}
Java
// Java program to construct a tree from level order and
// and inorder traversal
// A binary tree node
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
public void setLeft(Node left) { this.left = left; }
public void setRight(Node right) { this.right = right; }
}
class Tree {
Node root;
Node buildTree(int in[], int level[])
{
Node startnode = null;
return constructTree(startnode, level, in, 0,
in.length - 1);
}
Node constructTree(Node startNode, int[] levelOrder,
int[] inOrder, int inStart,
int inEnd)
{
// if start index is more than end index
if (inStart > inEnd)
return null;
if (inStart == inEnd)
return new Node(inOrder[inStart]);
boolean found = false;
int index = 0;
// it represents the index in inOrder array of
// element that appear first in levelOrder array.
for (int i = 0; i < levelOrder.length - 1; i++) {
int data = levelOrder[i];
for (int j = inStart; j < inEnd; j++) {
if (data == inOrder[j]) {
startNode = new Node(data);
index = j;
found = true;
break;
}
}
if (found == true)
break;
}
// elements present before index are part of left
// child of startNode. elements present after index
// are part of right child of startNode.
startNode.setLeft(
constructTree(startNode, levelOrder, inOrder,
inStart, index - 1));
startNode.setRight(
constructTree(startNode, levelOrder, inOrder,
index + 1, inEnd));
return startNode;
}
/* Utility function to print inorder traversal of binary
* tree */
void printInorder(Node node)
{
if (node == null)
return;
printInorder(node.left);
System.out.print(node.data + " ");
printInorder(node.right);
}
// Driver program to test the above functions
public static void main(String args[])
{
Tree tree = new Tree();
int in[] = new int[] { 4, 8, 10, 12, 14, 20, 22 };
int level[]
= new int[] { 20, 8, 22, 4, 12, 10, 14 };
int n = in.length;
Node node = tree.buildTree(in, level);
/* Let us test the built tree by printing Inorder
* traversal */
System.out.print(
"Inorder traversal of the constructed tree is ");
tree.printInorder(node);
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# Python program to construct tree using
# inorder and level order traversals
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, key):
self.data = key
self.left = None
self.right = None
"""Recursive function to construct binary tree of size n from
Inorder traversal ino[] and Level Order traversal level[].
The function doesn't do any error checking for cases
where inorder and levelorder do not form a tree """
def buildTree(level, ino):
# If ino array is not empty
if ino:
# Check if that element exist in level order
for i in range(0, len(level)):
if level[i] in ino:
# Create a new node with
# the matched element
node = Node(level[i])
# Get the index of the matched element
# in level order array
io_index = ino.index(level[i])
break
# Construct left and right subtree
node.left = buildTree(level, ino[0:io_index])
node.right = buildTree(level, ino[io_index + 1:len(ino)])
return node
else:
return None
def printInorder(node):
if node is None:
return
# first recur on left child
printInorder(node.left)
# then print the data of node
print(node.data, end=" ")
# now recur on right child
printInorder(node.right)
# Driver code
levelorder = [20, 8, 22, 4, 12, 10, 14]
inorder = [4, 8, 10, 12, 14, 20, 22]
ino_len = len(inorder)
root = buildTree(levelorder, inorder)
# Let us test the build tree by
# printing Inorder traversal
print("Inorder traversal of the constructed tree is")
printInorder(root)
# This code is contributed by 'Vaibhav Kumar'
C#
// C# program to construct a tree from
// level order and and inorder traversal
using System;
// A binary tree node
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
public virtual Node Left
{
set { this.left = value; }
}
public virtual Node Right
{
set { this.right = value; }
}
}
class GFG {
public Node root;
public virtual Node buildTree(int[] arr, int[] level)
{
Node startnode = null;
return constructTree(startnode, level, arr, 0,
arr.Length - 1);
}
public virtual Node
constructTree(Node startNode, int[] levelOrder,
int[] inOrder, int inStart, int inEnd)
{
// if start index is more than end index
if (inStart > inEnd) {
return null;
}
if (inStart == inEnd) {
return new Node(inOrder[inStart]);
}
bool found = false;
int index = 0;
// it represents the index in inOrder
// array of element that appear first
// in levelOrder array.
for (int i = 0; i < levelOrder.Length - 1; i++) {
int data = levelOrder[i];
for (int j = inStart; j < inEnd; j++) {
if (data == inOrder[j]) {
startNode = new Node(data);
index = j;
found = true;
break;
}
}
if (found == true) {
break;
}
}
// elements present before index are
// part of left child of startNode.
// elements present after index are
// part of right child of startNode.
startNode.Left
= constructTree(startNode, levelOrder, inOrder,
inStart, index - 1);
startNode.Right
= constructTree(startNode, levelOrder, inOrder,
index + 1, inEnd);
return startNode;
}
/* Utility function to print inorder
traversal of binary tree */
public virtual void printInorder(Node node)
{
if (node == null) {
return;
}
printInorder(node.left);
Console.Write(node.data + " ");
printInorder(node.right);
}
// Driver Code
public static void Main(string[] args)
{
GFG tree = new GFG();
int[] arr = new int[] { 4, 8, 10, 12, 14, 20, 22 };
int[] level
= new int[] { 20, 8, 22, 4, 12, 10, 14 };
int n = arr.Length;
Node node = tree.buildTree(arr, level);
/* Let us test the built tree by
printing Inorder traversal */
Console.Write("Inorder traversal of the "
+ "constructed tree is "
+ "\n");
tree.printInorder(node);
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// inorder and level order traversals
// A binary tree node
class Node{
// Constructor to create a new node
constructor(key){
this.data = key
this.left = null
this.right = null
}
}
// Recursive function to construct binary tree of size n from
// Inorder traversal ino[] and Level Order traversal level[].
// The function doesn't do any error checking for cases
// where inorder and levelorder do not form a tree
function buildTree(level, ino)
{
// If ino array is not empty
if(ino.length > 0)
{
// Check if that element exist in level order
let io_index;
let node;
for (let i = 0; i < level.length; i++)
{
if(ino.indexOf(level[i]) !== -1)
{
// Create a new node with
// the matched element
node = new Node(level[i])
// Get the index of the matched element
// in level order array
io_index = ino.indexOf(level[i]);
break
}
}
// Construct left and right subtree
node.left = buildTree(level, ino.slice(0,io_index))
node.right = buildTree(level, ino.slice(io_index+1,ino.length))
return node
}
else return null;
}
function printInorder(node){
if(node === null)
return
// first recur on left child
printInorder(node.left)
// then print the data of node
document.write(node.data," ")
// now recur on right child
printInorder(node.right)
}
// Driver code
let levelorder = [20, 8, 22, 4, 12, 10, 14];
let inorder = [4, 8, 10, 12, 14, 20, 22];
root = buildTree(levelorder, inorder);
// Let us test the build tree by
// printing Inorder traversal
document.write("Inorder traversal of the constructed tree is","</br>");
printInorder(root);
// This code is contributed by shinjanpatra
</script>
Inorder traversal of the constructed tree is 4 8 10 12 14 20 20
Un límite superior en la complejidad del tiempo del método anterior es O(n 3 ). En la función recursiva principal, se llama a extractNodes(), lo que lleva un tiempo O(n 2 ).
El código se puede optimizar de muchas maneras y puede haber mejores soluciones.
Complejidad de tiempo : O (n ^ 3)
Complejidad espacial: O(n) donde n es el número de Nodes.
Construir un árbol a partir de recorridos en orden Inorder y Level | conjunto 2
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA