Requisito previo: Árbol de segmentos y búsqueda en profundidad primero .
En este artículo, se analiza un enfoque para convertir un árbol con raíz N-aria (un árbol con más de 2 hijos) en un árbol de segmento que se utiliza para realizar consultas de actualización de rango.
¿Por qué necesitamos un árbol de segmentos cuando ya tenemos un árbol con raíces n-arias?
Muchas veces, ocurre una situación en la que se debe realizar la misma operación en múltiples Nodes y sus subárboles junto con operaciones de consulta varias veces.
Digamos que tenemos que realizar N actualizaciones en diferentes subárboles. Cada operación puede tardar hasta O(N), ya que es un árbol N-ario, por lo que la complejidad general será O(N^2), que es demasiado lenta para procesar más de 10^3 consultas de actualizaciones. Así que tenemos que ir al revés y construiremos un árbol de segmentos para lo mismo.
Enfoque: se realiza una primera búsqueda en profundidad para recorrer todos los Nodes y realizar un seguimiento de los índices del subárbol de cada Node en una array convertida utilizando dos arrays tin y tout (que serán el rango para realizar actualizaciones y consultas). El DFS realizará una caminata de Euler . La idea es crear una array y agregarle Nodes en el orden en que se visitan en la array convertida.
Veamos cómo las arrays tin y tout ayudan a determinar el rango en la array convertida.
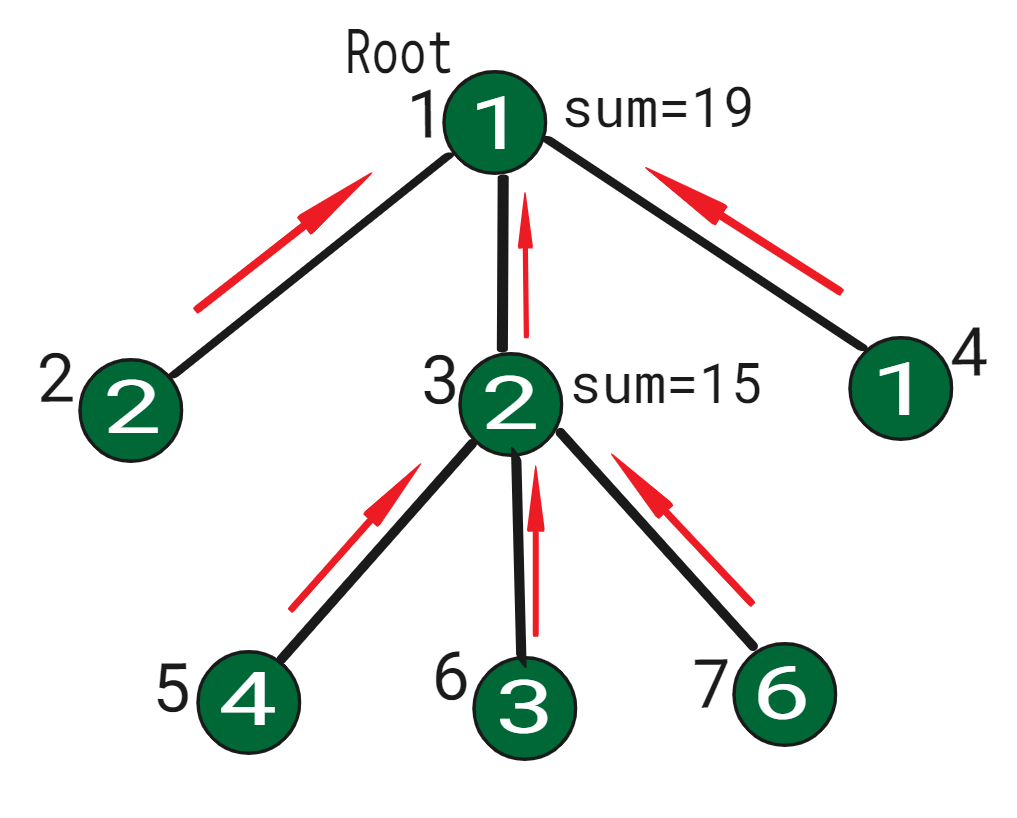
Sea N-árbol con raíces arias:
real values on nodes: 1 2 2 1 4 3 6 converted arr(indexes): 1 2 3 5 6 7 4 Node 3 has three children 5, 6, 7. Therefore, the range of node 3 is index 3-6. NODE: RANGE(tin-tout) NODE 1: 1 - 7 NODE 2: 2 - 2 NODE 3: 3 - 6 NODE 5: 4 - 4 NODE 6: 5 - 5 NODE 7: 6 - 6 NODE 4: 7 - 7
Aquí, el Node 1 tiene un rango de 1 a 7 (todos los Nodes), por lo que la actualización y la consulta se realizarán en todos los Nodes. Los Nodes de hoja como 2 que no tienen hijos solo actualizarán el rango 2-2 (solo en sí mismos), lo que demuestra que nuestras arrays de rango tin y tout son correctas. De manera similar, tin y tout para todos los Nodes determinan el rango de consulta y actualización en el árbol de segmentos.
La siguiente es la implementación del enfoque:
C++
// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define N 100005
// Keeping the values array indexed by 1.
int arr[8] = { 0, 1, 2, 2, 1, 4, 3, 6 };
vector<int> tree[N];
int idx, tin[N], tout[N], converted[N];
// Function to perform DFS in the tree
void dfs(ll node, ll parent)
{
++idx;
converted[idx] = node;
// To store starting range of a node
tin[node] = idx;
for (auto i : tree[node]) {
if (i != parent)
dfs(i, node);
}
// To store ending range of a node
tout[node] = idx;
}
// Segment tree
ll t[N * 4];
// Build using the converted array indexes.
// Here a simple n-ary tree is converted
// into a segment tree.
// Now O(NlogN) range updates and queries
// can be performed.
void build(ll node, ll start, ll end)
{
if (start == end)
t[node] = arr[converted[start]];
else {
ll mid = (start + end) >> 1;
build(2 * node, start, mid);
build(2 * node + 1, mid + 1, end);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to perform update operation
// on the tree
void update(ll node, ll start, ll end,
ll lf, ll rg, ll c)
{
if (start > end or start > rg or end < lf)
return;
if (start == end) {
t[node] = c;
}
else {
ll mid = (start + end) >> 1;
update(2 * node, start, mid, lf, rg, c);
update(2 * node + 1, mid + 1, end, lf, rg, c);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to find the sum at every node
ll query(ll node, ll start, ll end, ll lf, ll rg)
{
if (start > rg or end < lf)
return 0;
if (lf <= start and end <= rg) {
return t[node];
}
else {
ll ans = 0;
ll mid = (start + end) >> 1;
ans += query(2 * node, start, mid, lf, rg);
ans += query(2 * node + 1, mid + 1,
end, lf, rg);
return ans;
}
}
// Function to print the tree
void printTree(int q, int node, int n)
{
while (q--) {
// Calculating range of node in segment tree
ll lf = tin[node];
ll rg = tout[node];
ll res = query(1, 1, n, lf, rg);
cout << "sum at node " << node
<< ": " << res << endl;
node++;
}
}
// Driver code
int main()
{
int n = 7;
int q = 7;
// Creating the tree.
tree[1].pb(2);
tree[1].pb(3);
tree[1].pb(4);
tree[3].pb(5);
tree[3].pb(6);
tree[3].pb(7);
// DFS to get converted array.
idx = 0;
dfs(1, -1);
// Build segment tree with converted array.
build(1, 1, n);
printTree(7, 1, 7);
// Updating the value at node 3
int node = 3;
ll lf = tin[node];
ll rg = tout[node];
ll value = 4;
update(1, 1, n, lf, rg, value);
cout << "After Update" << endl;
printTree(7, 1, 7);
return 0;
}
Java
// Java implementation of the above approach
import java.util.*;
class GFG
{
static final int N = 100005;
// Keeping the values array indexed by 1.
static int arr[] = { 0, 1, 2, 2, 1, 4, 3, 6 };
static Vector<Integer> []tree = new Vector[N];
static int idx;
static int []tin = new int[N];
static int []tout = new int[N];
static int []converted = new int[N];
// Function to perform DFS in the tree
static void dfs(int node, int parent)
{
++idx;
converted[idx] = node;
// To store starting range of a node
tin[node] = idx;
for (int i : tree[node])
{
if (i != parent)
dfs(i, node);
}
// To store ending range of a node
tout[node] = idx;
}
// Segment tree
static int []t = new int[N * 4];
// Build using the converted array indexes.
// Here a simple n-ary tree is converted
// into a segment tree.
// Now O(NlogN) range updates and queries
// can be performed.
static void build(int node, int start, int end)
{
if (start == end)
t[node] = arr[converted[start]];
else
{
int mid = (start + end) >> 1;
build(2 * node, start, mid);
build(2 * node + 1, mid + 1, end);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to perform update operation
// on the tree
static void update(int node, int start, int end,
int lf, int rg, int c)
{
if (start > end || start > rg || end < lf)
return;
if (start == end)
{
t[node] = c;
}
else
{
int mid = (start + end) >> 1;
update(2 * node, start, mid, lf, rg, c);
update(2 * node + 1, mid + 1, end, lf, rg, c);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to find the sum at every node
static int query(int node, int start, int end,
int lf, int rg)
{
if (start > rg || end < lf)
return 0;
if (lf <= start && end <= rg)
{
return t[node];
}
else
{
int ans = 0;
int mid = (start + end) >> 1;
ans += query(2 * node, start, mid, lf, rg);
ans += query(2 * node + 1, mid + 1,
end, lf, rg);
return ans;
}
}
// Function to print the tree
static void printTree(int q, int node, int n)
{
while (q-- > 0)
{
// Calculating range of node in segment tree
int lf = tin[node];
int rg = tout[node];
int res = query(1, 1, n, lf, rg);
System.out.print("sum at node " + node
+ ": " + res +"\n");
node++;
}
}
// Driver code
public static void main(String[] args)
{
int n = 7;
int q = 7;
for(int i = 0; i < N; i++)
tree[i] = new Vector<Integer>();
// Creating the tree.
tree[1].add(2);
tree[1].add(3);
tree[1].add(4);
tree[3].add(5);
tree[3].add(6);
tree[3].add(7);
// DFS to get converted array.
idx = 0;
dfs(1, -1);
// Build segment tree with converted array.
build(1, 1, n);
printTree(7, 1, 7);
// Updating the value at node 3
int node = 3;
int lf = tin[node];
int rg = tout[node];
int value = 4;
update(1, 1, n, lf, rg, value);
System.out.print("After Update" + "\n");
printTree(7, 1, 7);
}
}
// This code is contributed by 29AjayKumar
Python3
# Python3 implementation of the above approach
N = 100005
# Keeping the values array indexed by 1.
arr = [0, 1, 2, 2, 1, 4, 3, 6]
tree = [[] for i in range(N)]
idx = 0
tin = [0]*N
tout = [0]*N
converted = [0]*N
# Function to perform DFS in the tree
def dfs(node, parent):
global idx
idx += 1
converted[idx] = node
# To store starting range of a node
tin[node] = idx
for i in tree[node]:
if (i != parent):
dfs(i, node)
# To store ending range of a node
tout[node] = idx
# Segment tree
t = [0]*(N * 4)
# Build using the converted array indexes.
# Here a simple n-ary tree is converted
# into a segment tree.
# Now O(NlogN) range updates and queries
# can be performed.
def build(node, start, end):
if (start == end):
t[node] = arr[converted[start]]
else:
mid = (start + end) >> 1
build(2 * node, start, mid)
build(2 * node + 1, mid + 1, end)
t[node] = t[2 * node] + t[2 * node + 1]
# Function to perform update operation
# on the tree
def update(node, start, end,lf, rg, c):
if (start > end or start > rg or end < lf):
return
if (start == end):
t[node] = c
else:
mid = (start + end) >> 1
update(2 * node, start, mid, lf, rg, c)
update(2 * node + 1, mid + 1, end, lf, rg, c)
t[node] = t[2 * node] + t[2 * node + 1]
# Function to find the sum at every node
def query(node, start, end, lf, rg):
if (start > rg or end < lf):
return 0
if (lf <= start and end <= rg):
return t[node]
else:
ans = 0
mid = (start + end) >> 1
ans += query(2 * node, start, mid, lf, rg)
ans += query(2 * node + 1, mid + 1,
end, lf, rg)
return ans
# Function to print tree
def printTree(q, node, n):
while (q > 0):
# Calculating range of node in segment tree
lf = tin[node]
rg = tout[node]
res = query(1, 1, n, lf, rg)
print("sum at node",node,":",res)
node += 1
q -= 1
# Driver code
if __name__ == '__main__':
n = 7
q = 7
# Creating the tree.
tree[1].append(2)
tree[1].append(3)
tree[1].append(4)
tree[3].append(5)
tree[3].append(6)
tree[3].append(7)
# DFS to get converted array.
idx = 0
dfs(1, -1)
# Build segment tree with converted array.
build(1, 1, n)
printTree(7, 1, 7)
# Updating the value at node 3
node = 3
lf = tin[node]
rg = tout[node]
value = 4
update(1, 1, n, lf, rg, value)
print("After Update")
printTree(7, 1, 7)
# This code is contributed by mohit kumar 29
C#
// C# implementation of the above approach
using System;
using System.Collections.Generic;
class GFG
{
static readonly int N = 100005;
// Keeping the values array indexed by 1.
static int []arr = { 0, 1, 2, 2, 1, 4, 3, 6 };
static List<int> []tree = new List<int>[N];
static int idx;
static int []tin = new int[N];
static int []tout = new int[N];
static int []converted = new int[N];
// Function to perform DFS in the tree
static void dfs(int node, int parent)
{
++idx;
converted[idx] = node;
// To store starting range of a node
tin[node] = idx;
foreach (int i in tree[node])
{
if (i != parent)
dfs(i, node);
}
// To store ending range of a node
tout[node] = idx;
}
// Segment tree
static int []t = new int[N * 4];
// Build using the converted array indexes.
// Here a simple n-ary tree is converted
// into a segment tree.
// Now O(NlogN) range updates and queries
// can be performed.
static void build(int node, int start, int end)
{
if (start == end)
t[node] = arr[converted[start]];
else
{
int mid = (start + end) >> 1;
build(2 * node, start, mid);
build(2 * node + 1, mid + 1, end);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to perform update operation
// on the tree
static void update(int node, int start, int end,
int lf, int rg, int c)
{
if (start > end || start > rg || end < lf)
return;
if (start == end)
{
t[node] = c;
}
else
{
int mid = (start + end) >> 1;
update(2 * node, start, mid, lf, rg, c);
update(2 * node + 1, mid + 1, end, lf, rg, c);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to find the sum at every node
static int query(int node, int start, int end,
int lf, int rg)
{
if (start > rg || end < lf)
return 0;
if (lf <= start && end <= rg)
{
return t[node];
}
else
{
int ans = 0;
int mid = (start + end) >> 1;
ans += query(2 * node, start, mid, lf, rg);
ans += query(2 * node + 1, mid + 1,
end, lf, rg);
return ans;
}
}
// Function to print the tree
static void printTree(int q, int node, int n)
{
while (q-- > 0)
{
// Calculating range of node in segment tree
int lf = tin[node];
int rg = tout[node];
int res = query(1, 1, n, lf, rg);
Console.Write("sum at node " + node
+ ": " + res +"\n");
node++;
}
}
// Driver code
public static void Main(String[] args)
{
int n = 7;
for(int i = 0; i < N; i++)
tree[i] = new List<int>();
// Creating the tree.
tree[1].Add(2);
tree[1].Add(3);
tree[1].Add(4);
tree[3].Add(5);
tree[3].Add(6);
tree[3].Add(7);
// DFS to get converted array.
idx = 0;
dfs(1, -1);
// Build segment tree with converted array.
build(1, 1, n);
printTree(7, 1, 7);
// Updating the value at node 3
int node = 3;
int lf = tin[node];
int rg = tout[node];
int value = 4;
update(1, 1, n, lf, rg, value);
Console.Write("After Update" + "\n");
printTree(7, 1, 7);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript implementation of the above approach
let N = 100005;
// Keeping the values array indexed by 1.
let arr = [ 0, 1, 2, 2, 1, 4, 3, 6];
let tree = new Array(N);
let idx;
let tin = new Array(N);
let tout = new Array(N);
let converted = new Array(N);
// Function to perform DFS in the tree
function dfs(node,parent)
{
++idx;
converted[idx] = node;
// To store starting range of a node
tin[node] = idx;
for (let i=0;i<tree[node].length;i++)
{
if (tree[node][i] != parent)
dfs(tree[node][i], node);
}
// To store ending range of a node
tout[node] = idx;
}
// Segment tree
let t = new Array(N * 4);
// Build using the converted array indexes.
// Here a simple n-ary tree is converted
// into a segment tree.
// Now O(NlogN) range updates and queries
// can be performed
function build(node,start,end)
{
if (start == end)
t[node] = arr[converted[start]];
else
{
let mid = (start + end) >> 1;
build(2 * node, start, mid);
build(2 * node + 1, mid + 1, end);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to perform update operation
// on the tree
function update(node,start,end,lf,rg,c)
{
if (start > end || start > rg || end < lf)
return;
if (start == end)
{
t[node] = c;
}
else
{
let mid = (start + end) >> 1;
update(2 * node, start, mid, lf, rg, c);
update(2 * node + 1, mid + 1, end, lf, rg, c);
t[node] = t[2 * node] + t[2 * node + 1];
}
}
// Function to find the sum at every node
function query(node,start,end,lf,rg)
{
if (start > rg || end < lf)
return 0;
if (lf <= start && end <= rg)
{
return t[node];
}
else
{
let ans = 0;
let mid = (start + end) >> 1;
ans += query(2 * node, start, mid, lf, rg);
ans += query(2 * node + 1, mid + 1,
end, lf, rg);
return ans;
}
}
// Function to print the tree
function printTree(q,node,n)
{
while (q-- > 0)
{
// Calculating range of node in segment tree
let lf = tin[node];
let rg = tout[node];
let res = query(1, 1, n, lf, rg);
document.write("sum at node " + node
+ ": " + res +"<br>");
node++;
}
}
// Driver code
let n = 7;
let q = 7;
for(let i = 0; i < N; i++)
tree[i] = [];
// Creating the tree.
tree[1].push(2);
tree[1].push(3);
tree[1].push(4);
tree[3].push(5);
tree[3].push(6);
tree[3].push(7);
// DFS to get converted array.
idx = 0;
dfs(1, -1);
// Build segment tree with converted array.
build(1, 1, n);
printTree(7, 1, 7);
// Updating the value at node 3
let node = 3;
let lf = tin[node];
let rg = tout[node];
let value = 4;
update(1, 1, n, lf, rg, value);
document.write("After Update" + "<br>");
printTree(7, 1, 7);
// This code is contributed by patel2127
</script>
sum at node 1: 19 sum at node 2: 2 sum at node 3: 15 sum at node 4: 1 sum at node 5: 4 sum at node 6: 3 sum at node 7: 6 After Update sum at node 1: 20 sum at node 2: 2 sum at node 3: 16 sum at node 4: 1 sum at node 5: 4 sum at node 6: 4 sum at node 7: 4
Tema relacionado: Árbol de segmentos