Construya un gráfico usando N vértices cuya distancia más corta entre K pares de vértices sea 2

Dados dos enteros positivos N y K , la tarea es construir un gráfico simple y conectado que consta de N vértices con la longitud de cada borde como 1 unidad, de modo que la distancia más corta entre exactamente K pares de vértices sea 2 . Si no es posible construir el gráfico, imprima -1 . De lo contrario, imprima los bordes del gráfico.

Ejemplos:

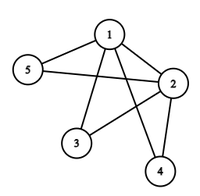
Entrada: N = 5, K = 3 
Salida: { { 1, 2 }, { 1, 3}, { 1, 4 }, { 1, 5 }, { 2, 3 }, { 2, 4 }, { 2 , 5 } } 
Explicación: 
La distancia entre los pares de vértices { (3, 4), (4, 5), (3, 5) } es 2. 
 

Entrada: N = 5, K = 8 
Salida: -1

Enfoque: siga los pasos a continuación para resolver el problema:

• Dado que el gráfico es simple y conectado, por lo tanto, el máximo número posible de aristas, por ejemplo, Max es ((N – 1) * (N – 2)) / 2 .
• Si K es mayor que Max , imprima -1 .
• Inicialice una array, digamos edge[] , para almacenar los bordes del gráfico.
• De lo contrario, primero conecta todos los vértices con 1 y guárdalo en edge[] , luego conecta todos los pares de vértices (i, j) de manera que i >= 2 y j > i y guárdalo en edge[] .
• Finalmente, imprima los primeros ((N – 1) + Max – K ) elementos de la array edge[] .

A continuación se muestra la implementación del enfoque anterior:

// C++ program to implement
// the above approach
 
#include <iostream>
#include <vector>
using namespace std;
 
// Function to construct the simple and
// connected graph such that the distance
// between exactly K pairs of vertices is 2
void constGraphWithCon(int N, int K)
{
 
    // Stores maximum possible count
    // of edges in a graph
    int Max = ((N - 1) * (N - 2)) / 2;
 
    // Base Case
    if (K > Max) {
        cout << -1 << endl;
        return;
    }
 
    // Stores edges of a graph
    vector<pair<int, int> > ans;
 
    // Connect all vertices of pairs (i, j)
    for (int i = 1; i < N; i++) {
        for (int j = i + 1; j <= N; j++) {
            ans.emplace_back(make_pair(i, j));
        }
    }
 
    // Print first ((N - 1) + Max - K)  elements
    // of edges[]
    for (int i = 0; i < (N - 1) + Max - K; i++) {
        cout << ans[i].first << " "
             << ans[i].second << endl;
    }
}
 
// Driver Code
int main()
{
    int N = 5, K = 3;
    constGraphWithCon(N, K);
 
    return 0;
}

// C program to implement
// the above approach
 
#include <stdio.h>
 
// Function to construct the simple and
// connected graph such that the distance
// between exactly K pairs of vertices is 2
void constGraphWithCon(int N, int K)
{
 
    // Stores maximum possible count
    // of edges in a graph
    int Max = ((N - 1) * (N - 2)) / 2;
 
    // Base Case
    if (K > Max) {
        printf("-1");
        return;
    }
 
    // Stores count of edges in a graph
    int count = 0;
 
    // Connect all vertices of pairs (i, j)
    for (int i = 1; i < N; i++) {
 
        for (int j = i + 1; j <= N; j++) {
 
            printf("%d %d\n", i, j);
 
            // Update
            count++;
 
            if (count == N * (N - 1) / 2 - K)
                break;
        }
 
        if (count == N * (N - 1) / 2 - K)
            break;
    }
}
 
// Driver Code
int main()
{
    int N = 5, K = 3;
    constGraphWithCon(N, K);
 
    return 0;
}

// Java program to implement
// the above approach
import java.util.*;
 
class GFG{
     
static class pair
{
    int first, second;
     
    public pair(int first, int second) 
    {
        this.first = first;
        this.second = second;
    }   
}
 
// Function to construct the simple and connected
// graph such that the distance between
// exactly K pairs of vertices is 2
static void constGraphWithCon(int N, int K)
{
     
    // Stores maximum possible count
    // of edges in a graph
    int Max = ((N - 1) * (N - 2)) / 2;
 
    // Base Case
    if (K > Max)
    {
        System.out.print(-1 + "\n");
        return;
    }
 
    // Stores edges of a graph
    Vector<pair> ans = new Vector<>();
 
    // Connect all vertices of pairs (i, j)
    for(int i = 1; i < N; i++)
    {
        for(int j = i + 1; j <= N; j++)
        {
            ans.add(new pair(i, j));
        }
    }
 
    // Print first ((N - 1) + Max - K)  elements
    // of edges[]
    for(int i = 0; i < (N - 1) + Max - K; i++)
    {
        System.out.print(ans.get(i).first + " " +
                         ans.get(i).second +"\n");
    }
}
 
// Driver Code
public static void main(String[] args)
{
    int N = 5, K = 3;
     
    constGraphWithCon(N, K);
}
}
 
// This code is contributed by 29AjayKumar

# Python3 program to implement
# the above approach
 
# Function to construct the simple and
# connected graph such that the distance
# between exactly K pairs of vertices is 2
def constGraphWithCon(N, K):
   
    # Stores maximum possible count
    # of edges in a graph
    Max = ((N - 1) * (N - 2)) // 2
     
    # Base case
    if (K > Max):
        print(-1)
        return
     
    # Stores edges of a graph
    ans = []
 
    # Connect all vertices of pairs (i, j)
    for i in range(1, N):
        for j in range(i + 1, N + 1):
            ans.append([i, j])
             
    # Print first ((N - 1) + Max - K)  elements
    # of edges[]
    for i in range(0, (N - 1) + Max - K):
        print(ans[i][0], ans[i][1], sep = " ")
 
# Driver code
if __name__ == '__main__':
     
    N = 5
    K = 3
     
    constGraphWithCon(N, K)
 
# This code is contributed by MuskanKalra1

// C# program to implement
// the above approach
using System;
using System.Collections.Generic;
 
public class GFG{
     
class pair
{
    public int first, second;
     
    public pair(int first, int second) 
    {
        this.first = first;
        this.second = second;
    }   
}
 
// Function to construct the simple and connected
// graph such that the distance between
// exactly K pairs of vertices is 2
static void constGraphWithCon(int N, int K)
{
     
    // Stores maximum possible count
    // of edges in a graph
    int Max = ((N - 1) * (N - 2)) / 2;
 
    // Base Case
    if (K > Max)
    {
        Console.Write(-1 + "\n");
        return;
    }
 
    // Stores edges of a graph
    List<pair> ans = new List<pair>();
 
    // Connect all vertices of pairs (i, j)
    for(int i = 1; i < N; i++)
    {
        for(int j = i + 1; j <= N; j++)
        {
            ans.Add(new pair(i, j));
        }
    }
 
    // Print first ((N - 1) + Max - K)  elements
    // of edges[]
    for(int i = 0; i < (N - 1) + Max - K; i++)
    {
        Console.Write(ans[i].first + " " +
                         ans[i].second +"\n");
    }
}
 
// Driver Code
public static void Main(String[] args)
{
    int N = 5, K = 3;
    constGraphWithCon(N, K);
}
}
 
// This code is contributed by 29AjayKumar

<script>
 
// Javascript program to implement
// the above approach
     
class pair
{
    constructor(first, second)
    {
        this[0] = first;
        this[1] = second;
    }
}
 
// Function to construct the simple and connected
// graph such that the distance between
// exactly K pairs of vertices is 2
function constGraphWithCon(N, K)
{
     
    // Stores maximum possible count
    // of edges in a graph
    var Max = ((N - 1) * (N - 2)) / 2;
 
    // Base Case
    if (K > Max)
    {
        document.write(-1 + "<br>");
        return;
    }
 
    // Stores edges of a graph
    var ans = [];
 
    // Connect all vertices of pairs (i, j)
    for(var i = 1; i < N; i++)
    {
        for(var j = i + 1; j <= N; j++)
        {
            ans.push([i, j]);
        }
    }
 
    // Print first ((N - 1) + Max - K)  elements
    // of edges[]
    for(var i = 0; i < (N - 1) + Max - K; i++)
    {
        document.write(ans[i][0] + " " +
                         ans[i][1] +"<br>");
    }
}
 
// Driver Code
var N = 5, K = 3;
constGraphWithCon(N, K);
 
</script>

1 2
1 3
1 4
1 5
2 3
2 4
2 5

Tiempo Complejidad: O(N ² )  
Espacio Auxiliar: O(N ² )