Requisito previo – Máquina de Turing
En el idioma dado L = {a i b j c k | yo < j < k; i≥ 1}, cada string de ‘a’, ‘b’ y ‘c’ tiene cierto número de a, luego cierto número de b y luego cierto número de c. La condición es que el recuento de los primeros símbolos debe ser al menos 1. ‘b’ y ‘c’ pueden tener a partir de entonces tantos pero el recuento de a es menor que el recuento de ‘b’ y el recuento de ‘b’ es menor que el recuento de ‘ C’. Suponga que la string termina con ‘$’.
Ejemplos:
Input: a a a b b c
Here a = 3, b = 2, c = 1 but |a|<|b|<|c|
Output: NOT ACCEPTED
Input: a b b c c c
Here a = 1, b = 2, c = 3
Output:ACCEPTED
Representación de cinta:

Acercarse:
- Comparando dos elementos haciendo D & C como un solo elemento.
- Después de eso Comparando D & C.
- Si |A| es mayor que |(D, C)|, entonces no se acepta.
- Si |C| es mayor que |D|, entonces no se acepta.
- De lo contrario, se acepta.
Pasos:
- Paso 1: Convierta A en X y muévase a la derecha y vaya al paso 2. Si encuentra Y, ignórelo y muévase a la derecha al paso 5.
- Paso 2: sigue ignorando A e Y y muévete hacia la derecha. Convierta D en Y y muévase a la derecha y vaya al paso 3.
- Paso 3: siga ignorando D y Z y muévase hacia la derecha. Si se encuentra C, hágalo Z y muévase hacia la izquierda hasta el paso 4.
- Paso 4: siga ignorando Z, A, Y y D y muévase hacia la izquierda. Si encuentra X, ignórelo, muévase a la derecha y vaya al paso 1.
- Paso 5: Sigue ignorando Y y muévete hacia la derecha. Ignore Z, muévase a la izquierda y vaya al paso 8. Si se encuentra D, conviértalo en Y y muévase a la derecha al paso 6.
- Paso 6: siga ignorando D y Z y muévase hacia la derecha. Convierta C en Z y muévase a la izquierda y vaya al paso 7.
- Paso 7: siga ignorando D y Z y muévase hacia la izquierda. Si encuentra Y, ignórelo, muévase a la derecha y vaya al paso 5.
- Paso 8: detener la máquina (se acepta la string)
Diagrama de transición de estado:
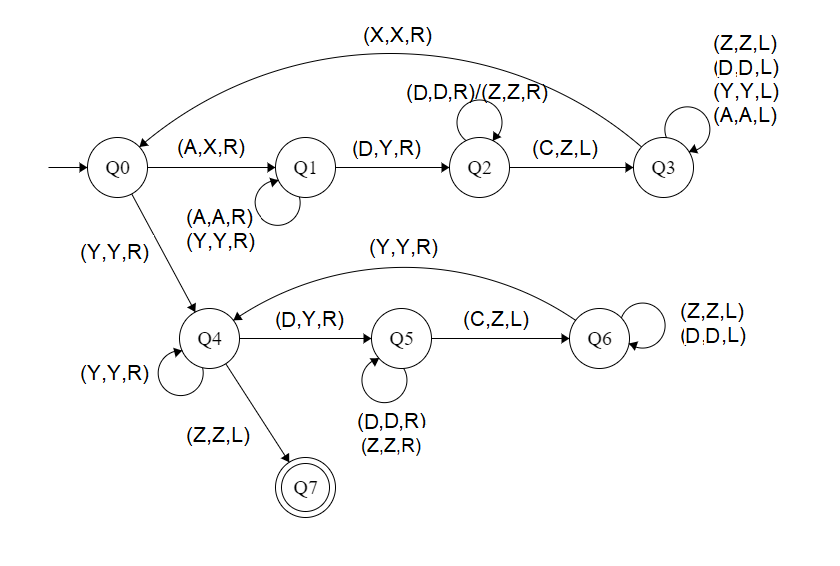
Aquí, Q0 muestra el estado inicial y Q1, Q2, Q3, Q4, Q5, Q6 muestra el estado de transición y Q7 muestra el estado final. A, C, D son las variables utilizadas y R, L muestra derecha e izquierda.
Explicación:
- Usando Q0, cuando se encuentre A, conviértalo en X y vaya a la derecha al estado Q1. Y, cuando se encuentre Y, ignórelo y vaya a la derecha y diga Q4
- En el estado Q1, ignore todo A e Y y vaya a la derecha. Si se encuentra D, conviértalo en Y y vaya directamente al siguiente estado Q2.
- En Q2, ignora todo D, Z y muévete a la derecha. Si se encuentra C, haga que Z se mueva hacia la izquierda y hacia Q3.
- En el estado Q3, ignora todo Z, D, Y, A y muévete a la izquierda. Si encuentra X, ignórelo y muévase a la derecha hasta Q0.
- En Q4, ignora todo Y y muévete a la derecha. Si encuentra Z, ignórelo, muévase hacia la izquierda hasta el estado Q6. Si se encuentra D, conviértalo en Y y muévase a la derecha hasta Q5.
- En el estado Q5, ignora todo D, Z y muévete a la derecha. Si se encuentra C, haga que Z se mueva hacia la izquierda hasta el estado Q6
- En Q6, ignora todo D, Z y muévete a la izquierda. Si encuentra Y, ignórelo y muévase a la derecha al estado Q4.
- Si se alcanza el estado Q7, producirá el resultado de la aceptación de la string.
Nota: Para la comparación de |A|, |D|, |C|, se utiliza el concepto de Máquina de Turing como Comparador .
Publicación traducida automáticamente
Artículo escrito por SHUBHAMSINGH10 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA