El término Redes Neuronalesse refiere al sistema de neuronas ya sea de naturaleza orgánica o artificial. En referencia a la inteligencia artificial, las redes neuronales son un conjunto de algoritmos que están diseñados para reconocer un patrón como un cerebro humano. Interpretan los datos sensoriales a través de una especie de entrada sin procesar de percepción, etiquetado o agrupación de máquinas. El reconocimiento es numérico, que se almacena en vectores, a los que se deben traducir todos los datos del mundo real, ya sean imágenes, sonido, texto o series temporales. Una red neuronal puede representarse como un sistema que consta de una serie de Nodes altamente interconectados, llamados «neuronas», que están organizados en capas que procesan información utilizando respuestas de estado dinámico a entradas externas. Antes de comprender el funcionamiento y la arquitectura de las redes neuronales, intentemos comprender qué son realmente las neuronas artificiales.
neuronas artificiales
Perceptrón: Los perceptrones son un tipo de neuronas artificiales desarrolladas en las décadas de 1950 y 1960 por el científico Frank Rosenbalt, inspirado en trabajos anteriores de Warren McCulloch y Walter Pitts. Entonces, ¿cómo funciona el perceptrón? Un perceptrón toma varias salidas binarias x 1 , x 2 , …., y produce una sola salida binaria.

Puede tener más o menos entradas. Calcular/calcular los pesos de salida juega un papel importante. Los pesos w 1 , w 2 , …., son números reales que expresan la importancia de las entradas respectivas a las salidas. La salida de la neurona (o o 1) depende totalmente de un valor de umbral y se calcula de acuerdo con la función:
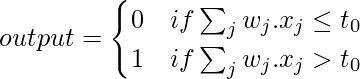
Aquí t 0 es el valor umbral. Es un número real que es un parámetro de la neurona. Ese es el modelo matemático básico. El perceptrón es que es un dispositivo que toma decisiones sopesando la evidencia. Al variar los pesos y el umbral, podemos obtener diferentes modelos de toma de decisiones.
Neuronas sigmoideas: las neuronas sigmoideas están mucho más cerca de los perceptrones, pero están modificadas para que pequeños cambios en sus pesos y sesgos causen solo un pequeño cambio en su salida. Permitirá que una red de neuronas sigmoideas aprenda de manera más eficiente. Al igual que un perceptrón, la neurona sigmoidea tiene entradas, x 1 , x 2 , …. Pero en lugar de ser solo 0 o 1, estas entradas también pueden tener cualquier valor entre 0 y 1. Entonces, por ejemplo, 0.567… es una entrada válida para una neurona sigmoidea. Una neurona sigmoidea también tiene pesos para cada entrada, w 1 , w 2 , …, y un sesgo general, b. Pero la salida no es 0 ni 1. En cambio, es σ(wx + b), donde σ se denomina función sigmoidea:
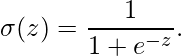
La salida de una neurona sigmoidea con entradas x 1 , x 2 , …, pesos w 1 , w 2 , … y sesgo b es:
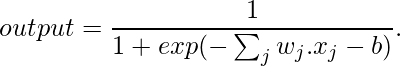
La arquitectura de las redes neuronales
Una red neuronal consta de tres capas:
- Capa de entrada: capas que toman entradas basadas en datos existentes.
- Capa oculta: capas que utilizan la retropropagación para optimizar los pesos de las variables de entrada con el fin de mejorar el poder predictivo del modelo.
- Capa de salida: salida de predicciones basadas en los datos de las capas de entrada y ocultas.

Los datos de entrada se introducen en la red neuronal a través de la capa de entrada que tiene una neurona por cada componente presente en los datos de entrada y se comunica a las capas ocultas (una o más) presentes en la red. Se llama ‘oculto’ solo porque no constituyen la capa de entrada o salida. En las capas ocultas, todo el procesamiento en realidad ocurre a través de un sistema de conexiones caracterizado por pesos y sesgos (como se discutió anteriormente). Una vez que se recibe la entrada, la neurona calcula una suma ponderada agregando también el sesgo y de acuerdo con el resultado y una función de activación (la más común es sigmoide), decide si debe ser ‘disparada’ o ‘activada’. Luego, la neurona transmite la información corriente abajo a otras neuronas conectadas en un proceso llamado «paso hacia adelante». Al final de este proceso,
Implementación de redes neuronales en programación R
Es mucho más fácil implementar una red neuronal utilizando el lenguaje R debido a sus excelentes bibliotecas en su interior. Antes de implementar una red neuronal en R, comprendamos primero la estructura de los datos.
Entender la estructura de los datos.
Aquí vamos a usar los conjuntos de datos binarios. El objetivo es predecir si un candidato será admitido en una universidad con variables como gre, gpa y rank. El script R se proporciona uno al lado del otro y se comenta para una mejor comprensión del usuario. Los datos están en formato .csv. Obtendremos el directorio de trabajo con la getwd()función y colocaremos conjuntos de datos binary.csv dentro de él para continuar. Descargue el archivo csv aquí .
# preparing the dataset
getwd()
data <- read.csv("binary.csv" )
str(data)
Producción:
'data.frame': 400 obs. of 4 variables: $ admit: int 0 1 1 1 0 1 1 0 1 0 ... $ gre : int 380 660 800 640 520 760 560 400 540 700 ... $ gpa : num 3.61 3.67 4 3.19 2.93 3 2.98 3.08 3.39 3.92 ... $ rank : int 3 3 1 4 4 2 1 2 3 2 ...
Al observar la estructura de los conjuntos de datos, podemos observar que tiene 4 variables, donde admitir indica si un candidato será admitido o no admitido (1 si es admitido y 0 si no es admitido) gre, gpa y rank le dan a los candidatos la puntuación gre, su /su gpa en la universidad anterior y el rango de la universidad anterior, respectivamente. Usamos admitir como variable dependiente y gre, gpa y rango como variables independientes. Ahora comprenda todo el proceso paso a paso.
Paso 1: Escalado de los datos
Para configurar una red neuronal a un conjunto de datos es muy importante que garanticemos un escalado adecuado de los datos. La escala de los datos es esencial porque, de lo contrario, una variable puede tener un gran impacto en la variable de predicción solo debido a su escala. El uso de datos sin escalar puede conducir a resultados sin sentido. Las técnicas comunes para escalar datos son la normalización min-max, la normalización de puntuación Z, la mediana y la MAD, y los estimadores tan-h. La normalización min-max transforma los datos en un rango común, eliminando así el efecto de escala de todas las variables. Aquí estamos usando la normalización min-max para escalar datos.
# Draw a histogram for gre data hist(data$gre)
Producción:
Del histograma anterior de gre podemos ver que el gre varía de 200 a 800. Invocamos la siguiente función para normalizar nuestros datos:
normalize <- function(x) {
return ((x - min(x)) / (max(x) - min(x)))
}
# Min-Max Normalization data$gre <- (data$gre - min(data$gre)) / (max(data$gre) - min(data$gre)) hist(data$gre)
Producción:
De la representación anterior podemos ver que los datos de gre se escalan en el rango de 0 a 1. Lo mismo hacemos para gpa y rango.
# Min-Max Normalization data$gpa <- (data$gpa - min(data$gpa)) / (max(data$gpa) - min(data$gpa)) hist(data$gpa) data$rank <- (data$rank - min(data$rank)) / (max(data$rank) - min(data$rank)) hist(data$rank)
Producción:
Se puede ver en las dos representaciones de histograma anteriores que el gpa y el rango también están escalados en el rango de 0 a 1. Los datos escalados se usan para ajustar la red neuronal.
Paso 2: Muestreo de los datos
Ahora divida los datos en un conjunto de entrenamiento y un conjunto de prueba. El conjunto de entrenamiento se utiliza para encontrar la relación entre las variables dependientes e independientes, mientras que el conjunto de prueba analiza el rendimiento del modelo. Utilizamos el 60% del conjunto de datos como conjunto de entrenamiento. La asignación de los datos al conjunto de entrenamiento y prueba se realiza mediante un muestreo aleatorio. Realizamos un muestreo aleatorio en R usando sample()la función. Úselo set.seed()para generar la misma muestra aleatoria cada vez y mantener la consistencia. Use la variable de índice mientras ajusta la red neuronal para crear conjuntos de datos de entrenamiento y prueba. El guión R es el siguiente:
set.seed(222) inp <- sample(2, nrow(data), replace = TRUE, prob = c(0.7, 0.3)) training_data <- data[inp==1, ] test_data <- data[inp==2, ]
Paso 3: Ajuste de una red neuronal
Ahora ajuste una red neuronal en nuestros datos. Usamos la biblioteca neuralnet para lo mismo. neuralnet()La función nos ayuda a establecer una red neuronal para nuestros datos. La neuralnet()función que estamos usando aquí tiene la siguiente sintaxis.
Sintaxis:
neuralnet(fórmula, datos, oculto = 1, stepmax = 1e+05, rep = 1, lifesign = “ninguno”, algoritmo = “rprop+”, err.fct = “sse”, linear.output = TRUE)
Parámetros:
| Argumento | Descripción |
|---|---|
| fórmula | una descripción simbólica del modelo a montar. |
| datos | un marco de datos que contiene las variables especificadas en la fórmula. |
| oculto | un vector de números enteros que especifica el número de neuronas ocultas (vértices) en cada capa |
| err.fct | una función diferenciable que se utiliza para el cálculo del error. Alternativamente, se pueden usar las strings ‘sse’ y ‘ce’ que representan la suma de los errores al cuadrado y la entropía cruzada. |
| salida.lineal | lógico. Si act.fct no se debe aplicar a las neuronas de salida, establezca la salida lineal en VERDADERO; de lo contrario, en FALSO. |
| señal de vida | una string que especifica cuánto imprimirá la función durante el cálculo de la red neuronal. ‘ninguno’, ‘mínimo’ o ‘completo’. |
| reps | el número de repeticiones para el entrenamiento de la red neuronal. |
| algoritmo | una string que contiene el tipo de algoritmo para calcular la red neuronal. Son posibles los siguientes tipos: ‘backprop’, ‘rprop+’, ‘rprop-‘, ‘sag’ o ‘slr’. ‘backprop’ se refiere a la retropropagación, ‘rprop+’ y ‘rprop-‘ se refieren a la retropropagación resistente con y sin retroceso de peso, mientras que ‘sag’ y ‘slr’ inducen el uso del algoritmo convergente global modificado (grprop). |
| paso máximo | los pasos máximos para el entrenamiento de la red neuronal. Alcanzar este máximo conduce a una detención del proceso de entrenamiento de la red neuronal. |
library(neuralnet) set.seed(333) n <- neuralnet(admit~gre + gpa + rank, data = training_data, hidden = 5, err.fct = "ce", linear.output = FALSE, lifesign = 'full', rep = 2, algorithm = "rprop+", stepmax = 100000)
hidden: 5 thresh: 0.01 rep: 1/2 steps: 1000 min thresh: 0.092244246452834
2000 min thresh: 0.092244246452834
3000 min thresh: 0.092244246452834
4000 min thresh: 0.092244246452834
5000 min thresh: 0.092244246452834
6000 min thresh: 0.092244246452834
7000 min thresh: 0.092244246452834
8000 min thresh: 0.0657773918077728
9000 min thresh: 0.0492128119805471
10000 min thresh: 0.0350341801886022
11000 min thresh: 0.0257113452845989
12000 min thresh: 0.0175961794629306
13000 min thresh: 0.0108791716102531
13253 error: 139.80883 time: 7.51 secs
hidden: 5 thresh: 0.01 rep: 2/2 steps: 1000 min thresh: 0.147257381292693
2000 min thresh: 0.147257381292693
3000 min thresh: 0.091389043508166
4000 min thresh: 0.0648814957085886
5000 min thresh: 0.0472858320232246
6000 min thresh: 0.0359632940146351
7000 min thresh: 0.0328699898176084
8000 min thresh: 0.0305035254157369
9000 min thresh: 0.0305035254157369
10000 min thresh: 0.0241743801258625
11000 min thresh: 0.0182557959333173
12000 min thresh: 0.0136844933371039
13000 min thresh: 0.0120885410813301
14000 min thresh: 0.0109156031403791
14601 error: 147.41304 time: 8.25 secs
Del resultado anterior concluimos que ambas repeticiones convergen. Pero usaremos la salida impulsada en la primera repetición porque da menos error (139.80883) que el error (147.41304) derivado de la segunda repetición. Ahora, tracemos nuestra red neuronal y visualicemos la red neuronal computada.
# plot our neural network plot(n, rep = 1)
Producción:
El modelo tiene 5 neuronas en su capa oculta. Las líneas negras muestran las conexiones con pesos. Los pesos se calculan utilizando el algoritmo de retropropagación. La línea azul muestra el término de sesgo (constante en una ecuación de regresión). Ahora genere el error del modelo de red neuronal, junto con los pesos entre las entradas, las capas ocultas y las salidas:
# error n$result.matrix
Producción:
[, 1] [, 2] error 1.398088e+02 1.474130e+02 reached.threshold 9.143429e-03 9.970574e-03 steps 1.325300e+04 1.460100e+04 Intercept.to.1layhid1 -6.713132e+01 -1.136151e+02 gre.to.1layhid1 -2.448706e+01 1.469138e+02 gpa.to.1layhid1 8.326628e+01 1.290251e+02 rank.to.1layhid1 2.974782e+01 -5.733805e+01 Intercept.to.1layhid2 -2.582341e+01 2.508958e-01 gre.to.1layhid2 -5.800955e+01 1.302115e+00 gpa.to.1layhid2 3.206933e+01 -4.856419e+00 rank.to.1layhid2 6.723053e+01 1.540390e+01 Intercept.to.1layhid3 3.174853e+01 -3.495968e+01 gre.to.1layhid3 1.050214e+01 1.325498e+02 gpa.to.1layhid3 -6.478704e+01 -4.536649e+01 rank.to.1layhid3 -7.706895e+01 -1.844943e+02 Intercept.to.1layhid4 1.625662e+01 2.188646e+01 gre.to.1layhid4 -3.552645e+01 1.956271e+01 gpa.to.1layhid4 -1.151684e+01 2.052294e+01 rank.to.1layhid4 -2.263859e+01 1.347474e+01 Intercept.to.1layhid5 2.448949e+00 -3.978068e+01 gre.to.1layhid5 -2.924269e+00 -1.569897e+02 gpa.to.1layhid5 -7.773543e+00 1.500767e+02 rank.to.1layhid5 -1.107282e+03 4.045248e+02 Intercept.to.admit -5.480278e-01 -3.622384e+00 1layhid1.to.admit 1.580944e+00 1.717584e+00 1layhid2.to.admit -1.943969e+00 -6.195182e+00 1layhid3.to.admit -5.137650e+01 6.731498e+00 1layhid4.to.admit -1.112174e+03 -4.245278e+00 1layhid5.to.admit 7.259237e+02 1.156083e+01
Paso 4: Predicción
Predigamos la calificación usando el modelo de red neuronal. Debemos recordar que la calificación pronosticada estará escalada y deberá transformarse para poder hacer una comparación con la calificación real. También compare la calificación predicha con la calificación real.
# Prediction output <- compute(n, rep = 1, training_data[, -1]) head(output$net.result)
Producción:
[, 1]
2 0.34405929
3 0.41148373
4 0.07642387
7 0.98152454
8 0.26230256
9 0.07660906
head(training_data[1, ])
Producción:
admit gre gpa rank 2 1 0.7586207 0.8103448 0.6666667
Paso 5: Array de confusión y error de clasificación errónea
Luego, redondeamos nuestros resultados usando el compute()método y creamos una array de confusión para comparar el número de verdaderos/falsos positivos y negativos. Formaremos una array de confusión con datos de entrenamiento
# confusion Matrix $Misclassification error -Training data output <- compute(n, rep = 1, training_data[, -1]) p1 <- output$net.result pred1 <- ifelse(p1 > 0.5, 1, 0) tab1 <- table(pred1, training_data$admit) tab1
Producción:
pred1 0 1
0 177 58
1 12 34
El modelo genera 177 verdaderos negativos (0), 34 verdaderos positivos (1), mientras que hay 12 falsos negativos y 58 falsos positivos. Ahora, calculemos el error de clasificación errónea (para datos de entrenamiento) que {1 – error de clasificación}
1 - sum(diag(tab1)) / sum(tab1)
Producción:
[1] 0.2491103
El error de clasificación errónea resulta ser del 24,9%. Podemos aumentar aún más la precisión y la eficiencia de nuestro modelo aumentando los Nodes decrecientes y el sesgo en las capas ocultas.
La fuerza de los algoritmos de aprendizaje automático radica en su capacidad para aprender y mejorar cada vez que predicen un resultado. En el contexto de las redes neuronales, implica que los pesos y sesgos que definen la conexión entre neuronas se vuelven más precisos. Esta es la razón por la cual los pesos y sesgos se seleccionan de manera que la salida de la red se aproxime al valor real de todas las entradas de entrenamiento. De manera similar, podemos hacer modelos de redes neuronales más eficientes en R para predecir e impulsar decisiones.
Publicación traducida automáticamente
Artículo escrito por misraaakash1998 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA




