Consultas de valores decimales de subarreglos de un arreglo binario

Dado un arreglo binario arr[], buscamos el número representado por el subarreglo a[l..r]. Hay múltiples consultas de este tipo.

Ejemplos: 

Input :  arr[] = {1, 0, 1, 0, 1, 1};
         l = 2, r = 4
         l = 4, r = 5
Output : 5
         3 
Subarray 2 to 4 is 101 which is 5 in decimal.
Subarray 4 to 5 is 11 which is 3 in decimal.

Input : arr[] = {1, 1, 1}
        l = 0, r = 2
        l = 1, r = 2
Output : 7
         3

Una solución simple es calcular el valor decimal para cada rango dado usando una conversión simple de binario a decimal. Aquí, cada consulta toma el tiempo O (len) donde len es la longitud del rango.

Una Solución Eficiente es hacer por-cómputos, para que las consultas puedan ser respondidas en tiempo O(1). 

El número representado por el subarreglo arr[l..r] es arr[l]* + arr[l+1]* ….. + arr[r]*

1. Cree una array pre[] del mismo tamaño que la array dada donde pre[i] almacena la suma de arr[j]* 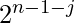donde j incluye cada valor de i a n-1.
2. El número representado por el subarreglo arr[l..r] será igual a (pre[l] – pre[r+1])/ 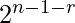.pre[l] – pre[r+1] es igual a arr[l]* + arr[l+1]* 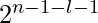+……arr[r]* 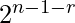. Entonces, si lo dividimos por  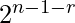, obtenemos la respuesta requerida

 diagrama de flujo

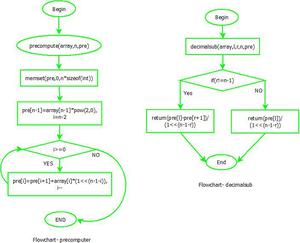
diagrama de flujo

Implementación:

// C++ implementation of finding number
// represented by binary subarray
#include <bits/stdc++.h>
using namespace std;
 
// Fills pre[]
void precompute(int arr[], int n, int pre[])
{
    memset(pre, 0, n * sizeof(int));
    pre[n - 1] = arr[n - 1] * pow(2, 0);
    for (int i = n - 2; i >= 0; i--)
        pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
}
 
// returns the number represented by a binary
// subarray l to r
int decimalOfSubarr(int arr[], int l, int r,
                    int n, int pre[])
{
    // if r is equal to n-1 r+1 does not exist
    if (r != n - 1)
        return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));
 
    return pre[l] / (1 << (n - 1 - r));
}
 
// Driver Function
int main()
{
    int arr[] = { 1, 0, 1, 0, 1, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    int pre[n];
    precompute(arr, n, pre);
    cout << decimalOfSubarr(arr, 2, 4, n, pre) << endl;
    cout << decimalOfSubarr(arr, 4, 5, n, pre) << endl;
    return 0;
}

// Java implementation of finding number
// represented by binary subarray
import java.util.Arrays;
 
class GFG {
 
    // Fills pre[]
    static void precompute(int arr[], int n, int pre[])
    {
        Arrays.fill(pre, 0);
 
        pre[n - 1] = arr[n - 1] * (int)(Math.pow(2, 0));
        for (int i = n - 2; i >= 0; i--)
            pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
    }
 
    // returns the number represented by a binary
    // subarray l to r
    static int decimalOfSubarr(int arr[], int l, int r,
                               int n, int pre[])
    {
 
        // if r is equal to n-1 r+1 does not exist
        if (r != n - 1)
            return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));
 
        return pre[l] / (1 << (n - 1 - r));
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 1, 0, 1, 0, 1, 1 };
        int n = arr.length;
 
        int pre[] = new int[n];
        precompute(arr, n, pre);
 
        System.out.println(decimalOfSubarr(arr,
                                           2, 4, n, pre));
 
        System.out.println(decimalOfSubarr(arr,
                                           4, 5, n, pre));
    }
}
 
// This code is contributed by Anant Agarwal.

# implementation of finding number
# represented by binary subarray
from math import pow
 
# Fills pre[]
def precompute(arr, n, pre):
     
    pre[n - 1] = arr[n - 1] * pow(2, 0)
    i = n - 2
    while(i >= 0):
        pre[i] = (pre[i + 1] + arr[i] *
                 (1 << (n - 1 - i)))
        i -= 1
 
# returns the number represented by
# a binary subarray l to r
def decimalOfSubarr(arr, l, r, n, pre):
     
    # if r is equal to n-1 r+1 does not exist
    if (r != n - 1):
        return ((pre[l] - pre[r + 1]) /
                (1 << (n - 1 - r)))
 
    return pre[l] / (1 << (n - 1 - r))
 
# Driver Code
if __name__ == '__main__':
    arr = [1, 0, 1, 0, 1, 1]
    n = len(arr)
 
    pre = [0 for i in range(n)]
    precompute(arr, n, pre)
    print(int(decimalOfSubarr(arr, 2, 4, n, pre)))
    print(int(decimalOfSubarr(arr, 4, 5, n, pre)))
 
# This code is contributed by
# Surendra_Gangwar

// C# implementation of finding number
// represented by binary subarray
using System;
 
class GFG {
 
    // Fills pre[]
    static void precompute(int[] arr, int n, int[] pre)
    {
        for (int i = 0; i < n; i++)
            pre[i] = 0;
 
        pre[n - 1] = arr[n - 1] * (int)(Math.Pow(2, 0));
        for (int i = n - 2; i >= 0; i--)
            pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
    }
 
    // returns the number represented by
    // a binary subarray l to r
    static int decimalOfSubarr(int[] arr, int l, int r,
                                      int n, int[] pre)
    {
        // if r is equal to n-1 r+1 does not exist
        if (r != n - 1)
            return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));
 
        return pre[l] / (1 << (n - 1 - r));
    }
 
    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 0, 1, 0, 1, 1 };
        int n = arr.Length;
 
        int[] pre = new int[n];
        precompute(arr, n, pre);
 
        Console.WriteLine(decimalOfSubarr(arr,
                                        2, 4, n, pre));
 
        Console.WriteLine(decimalOfSubarr(arr,
                                        4, 5, n, pre));
    }
}
 
// This code is contributed by vt_m.

<?php
// PHP implementation of finding number
// represented by binary subarray
 
// Fills pre[]
function precompute(&$arr, $n, &$pre)
{
    $pre[$n - 1] = $arr[$n - 1] * pow(2, 0);
    for ($i = $n - 2; $i >= 0; $i--)
        $pre[$i] = $pre[$i + 1] + $arr[$i] *
                           (1 << ($n - 1 - $i));
}
 
// returns the number represented by
// a binary subarray l to r
function decimalOfSubarr(&$arr, $l, $r, $n, &$pre)
{
    // if r is equal to n-1 r+1 does not exist
    if ($r != $n - 1)
        return ($pre[$l] - $pre[$r + 1]) /
                    (1 << ($n - 1 - $r));
 
    return $pre[$l] / (1 << ($n - 1 - $r));
}
 
// Driver Code
$arr = array(1, 0, 1, 0, 1, 1 );
$n = sizeof($arr);
 
$pre = array_fill(0, $n, NULL);
precompute($arr, $n, $pre);
echo decimalOfSubarr($arr, 2, 4, $n, $pre) . "\n";
echo decimalOfSubarr($arr, 4, 5, $n, $pre) . "\n";
 
// This code is contributed by ita_c
?>

<script>
 
// Javascript implementation of finding number
// represented by binary subarray
 
 
// Fills pre[]
function precompute(arr, n, pre)
{
    for (let i = 0; i < n; i++)
        pre[i] = 0;
 
    pre[n - 1] = arr[n - 1] * (Math.pow(2, 0));
    for (let i = n - 2; i >= 0; i--)
        pre[i] = pre[i + 1] + arr[i] *
                 (1 << (n - 1 - i));
}
 
// returns the number represented by
// a binary subarray l to r
function decimalOfSubarr(arr, l, r,n, pre)
{
    // if r is equal to n-1 r+1 does not exist
    if (r != n - 1)
        return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));
 
    return pre[l] / (1 << (n - 1 - r));
}
 
// Driver code
 
let arr = [1, 0, 1, 0, 1, 1];
let n = arr.length;
 
let pre = new Array(n)
precompute(arr, n, pre);
 
document.write(decimalOfSubarr(arr,2, 4, n, pre)+"<br>");
 
document.write(decimalOfSubarr(arr, 4, 5, n, pre));
 
</script>

5
3

Complejidad temporal: O(n)
Espacio auxiliar: O(n)

Este artículo es una contribución de Ayush Jha . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.