Dado un árbol de N Nodes y N-1 aristas. La tarea es imprimir el DFS del subárbol de un Node dado para múltiples consultas. El DFS debe incluir el Node dado como la raíz del subárbol.
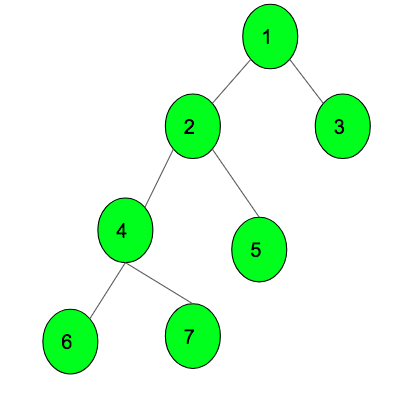
En el árbol anterior, si se da 1 como Node, entonces el DFS del subárbol será 1 2 4 6 7 5 3 .
Si se da 2 como Node, entonces el DFS del subárbol será 2 4 6 7 5. .
Acercarse:
- Agregue los bordes entre los Nodes en una lista de adyacencia.
- Llame a la función DFS para generar el DFS del árbol completo.
- Use una array under[] para almacenar la altura del subárbol debajo del Node dado, incluido el Node.
- En la función DFS, siga incrementando el tamaño del subárbol en cada llamada recursiva.
- Marque el índice de Node en el DFS de completo usando hashing.
- El DFS de un subárbol de un Node siempre será un subarreglo contiguo que comienza desde el Node ( por ejemplo, index ind ) hasta (ind+height of subtree) .
- Obtenga el índice del Node que se almacenó usando hashing e imprima los Nodes desde el DFS original hasta el índice = ind + altura del subárbol que se almacenó en debajo de [Node].
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program for Queries
// for DFS of subtree of a node in a tree
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
// Adjacency list to store the
// tree nodes connection
vector<int> v[N];
// stores the index of node in DFS
unordered_map<int, int> mp;
// stores the index of node in
// original node
vector<int> a;
// Function to call DFS and count nodes
// under that subtree
void dfs(int under[], int child, int parent)
{
// stores the DFS of tree
a.push_back(child);
// height of subtree
under[child] = 1;
// iterate for children
for (auto it : v[child]) {
// if not equal to parent
// so that it does not traverse back
if (it != parent) {
// call DFS for subtree
dfs(under, it, child);
// add the height
under[child] += under[it];
}
}
}
// Function to print the DFS of subtree of node
void printDFSofSubtree(int node, int under[])
{
// index of node in the original DFS
int ind = mp[node];
// height of subtree of node
int height = under[node];
cout << "The DFS of subtree " << node << ": ";
// print the DFS of subtree
for (int i = ind; i < ind + under[node]; i++) {
cout << a[i] << " ";
}
cout << endl;
}
// Function to add edges to a tree
void addEdge(int x, int y)
{
v[x].push_back(y);
v[y].push_back(x);
}
// Marks the index of node in original DFS
void markIndexDfs()
{
int size = a.size();
// marks the index
for (int i = 0; i < size; i++) {
mp[a[i]] = i;
}
}
// Driver Code
int main()
{
int n = 7;
// add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// array to store the height of subtree
// of every node in a tree
int under[n + 1];
// Call the function DFS to generate the DFS
dfs(under, 1, 0);
// Function call to mark the index of node
markIndexDfs();
// Query 1
printDFSofSubtree(2, under);
// Query 1
printDFSofSubtree(4, under);
return 0;
}
Java
// Java program for queries for DFS
// of subtree of a node in a tree
import java.util.*;
class GFG{
static int N = 100000;
// Adjacency list to store the
// tree nodes connection
@SuppressWarnings("unchecked")
static Vector<Integer> []v = new Vector[N];
// Stores the index of node in DFS
static HashMap<Integer,
Integer> mp = new HashMap<Integer,
Integer>();
// Stores the index of node in
// original node
static Vector<Integer> a = new Vector<>();
// Function to call DFS and count nodes
// under that subtree
static void dfs(int under[], int child,
int parent)
{
// Stores the DFS of tree
a.add(child);
// Height of subtree
under[child] = 1;
// Iterate for children
for(int it : v[child])
{
// If not equal to parent so that
// it does not traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// Add the height
under[child] += under[it];
}
}
}
// Function to print the DFS of subtree of node
static void printDFSofSubtree(int node, int under[])
{
// Index of node in the original DFS
int ind = mp.get(node);
// Height of subtree of node
int height = under[node];
System.out.print("The DFS of subtree " +
node + ": ");
// Print the DFS of subtree
for(int i = ind; i < ind + under[node]; i++)
{
System.out.print(a.get(i) + " ");
}
System.out.println();
}
// Function to add edges to a tree
static void addEdge(int x, int y)
{
v[x].add(y);
v[y].add(x);
}
// Marks the index of node in original DFS
static void markIndexDfs()
{
int size = a.size();
// Marks the index
for(int i = 0; i < size; i++)
{
mp.put(a.get(i), i);
}
}
// Driver Code
public static void main(String[] args)
{
int n = 7;
for(int i = 0; i < v.length; i++)
v[i] = new Vector<Integer>();
// Add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height of
// subtree of every node in a tree
int []under = new int[n + 1];
// Call the function DFS to
// generate the DFS
dfs(under, 1, 0);
// Function call to mark the
// index of node
markIndexDfs();
// Query 1
printDFSofSubtree(2, under);
// Query 1
printDFSofSubtree(4, under);
}
}
// This code is contributed by Amit Katiyar
Python3
# Python3 program for Queries
# for DFS of subtree of a node in a tree
N = 100000
# Adjacency list to store the
# tree nodes connection
v = [[]for i in range(N)]
# stores the index of node in DFS
mp = {}
# stores the index of node in
# original node
a = []
# Function to call DFS and count nodes
# under that subtree
def dfs(under, child, parent):
# stores the DFS of tree
a.append(child)
# height of subtree
under[child] = 1
# iterate for children
for it in v[child]:
# if not equal to parent
# so that it does not traverse back
if (it != parent):
# call DFS for subtree
dfs(under, it, child)
# add the height
under[child] += under[it]
# Function to return the DFS of subtree of node
def printDFSofSubtree(node, under):
# index of node in the original DFS
ind = mp[node]
# height of subtree of node
height = under[node]
print("The DFS of subtree", node, ":", end=" ")
# print the DFS of subtree
for i in range(ind,ind + under[node]):
print(a[i], end=" ")
print()
# Function to add edges to a tree
def addEdge(x, y):
v[x].append(y)
v[y].append(x)
# Marks the index of node in original DFS
def markIndexDfs():
size = len(a)
# marks the index
for i in range(size):
mp[a[i]] = i
# Driver Code
n = 7
# add edges of a tree
addEdge(1, 2)
addEdge(1, 3)
addEdge(2, 4)
addEdge(2, 5)
addEdge(4, 6)
addEdge(4, 7)
# array to store the height of subtree
# of every node in a tree
under = [0]*(n + 1)
# Call the function DFS to generate the DFS
dfs(under, 1, 0)
# Function call to mark the index of node
markIndexDfs()
# Query 1
printDFSofSubtree(2, under)
# Query 2
printDFSofSubtree(4, under)
# This code is contributed by SHUBHAMSINGH10
C#
// C# program for queries for DFS
// of subtree of a node in a tree
using System;
using System.Collections.Generic;
class GFG{
static int N = 100000;
// Adjacency list to
// store the tree nodes
// connection
static List<int> []v =
new List<int>[N];
// Stores the index of node in DFS
static Dictionary<int,
int> mp = new Dictionary<int,
int>();
// Stores the index of node in
// original node
static List<int> a = new List<int>();
// Function to call DFS and
// count nodes under that
// subtree
static void dfs(int []under,
int child,
int parent)
{
// Stores the DFS of tree
a.Add(child);
// Height of subtree
under[child] = 1;
// Iterate for children
foreach(int it in v[child])
{
// If not equal to parent
// so that it does not
// traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// Add the height
under[child] += under[it];
}
}
}
// Function to print the DFS of
// subtree of node
static void printDFSofSubtree(int node,
int []under)
{
// Index of node in the
// original DFS
int ind = mp[node];
// Height of subtree of node
int height = under[node];
Console.Write("The DFS of subtree " +
node + ": ");
// Print the DFS of subtree
for(int i = ind;
i < ind + under[node]; i++)
{
Console.Write(a[i] + " ");
}
Console.WriteLine();
}
// Function to add edges
// to a tree
static void addEdge(int x,
int y)
{
v[x].Add(y);
v[y].Add(x);
}
// Marks the index of node
// in original DFS
static void markIndexDfs()
{
int size = a.Count;
// Marks the index
for(int i = 0; i < size; i++)
{
mp.Add(a[i], i);
}
}
// Driver Code
public static void Main(String[] args)
{
int n = 7;
for(int i = 0; i < v.Length; i++)
v[i] = new List<int>();
// Add edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height
// of subtree of every node
// in a tree
int []under = new int[n + 1];
// Call the function DFS to
// generate the DFS
dfs(under, 1, 0);
// Function call to mark the
// index of node
markIndexDfs();
// Query 1
printDFSofSubtree(2, under);
// Query 1
printDFSofSubtree(4, under);
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// Javascript program for queries for DFS
// of subtree of a node in a tree
var N = 100000;
// Adjacency list to
// store the tree nodes
// connection
var v = Array.from(Array(N), () => Array());
// Stores the index of node in DFS
var mp = new Map();
// Stores the index of node in
// original node
var a = [];
// Function to call DFS and
// count nodes under that
// subtree
function dfs(under, child, parent)
{
// Stores the DFS of tree
a.push(child);
// Height of subtree
under[child] = 1;
// Iterate for children
for(var it of v[child])
{
// If not equal to parent
// so that it does not
// traverse back
if (it != parent)
{
// Call DFS for subtree
dfs(under, it, child);
// push the height
under[child] += under[it];
}
}
}
// Function to print the DFS of
// subtree of node
function printDFSofSubtree(node, under)
{
// Index of node in the
// original DFS
var ind = mp.get(node);
// Height of subtree of node
var height = under[node];
document.write("The DFS of subtree " +
node + ": ");
// Print the DFS of subtree
for(var i = ind;
i < ind + under[node]; i++)
{
document.write(a[i] + " ");
}
document.write("<br>");
}
// Function to add edges
// to a tree
function addEdge(x, y)
{
v[x].push(y);
v[y].push(x);
}
// Marks the index of node
// in original DFS
function markIndexDfs()
{
var size = a.length;
// Marks the index
for(var i = 0; i < size; i++)
{
mp.set(a[i], i);
}
}
// Driver Code
var n = 7;
for(var i = 0; i < v.length; i++)
v[i] = Array();
// push edges of a tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(4, 6);
addEdge(4, 7);
// Array to store the height
// of subtree of every node
// in a tree
var under = Array(n + 1);
// Call the function DFS to
// generate the DFS
dfs(under, 1, 0);
// Function call to mark the
// index of node
markIndexDfs();
// Query 1
printDFSofSubtree(2, under);
// Query 1
printDFSofSubtree(4, under);
// This code is contributed by rutvik_56
</script>
Producción:
The DFS of subtree 2: 2 4 6 7 5 The DFS of subtree 4: 4 6 7
Complejidad Temporal: O( N + M ), donde N es el número de Nodes y M es el número de aristas para precálculo, y O(N) para consultas en el peor de los casos.
Espacio Auxiliar: O(N)