Dado un árbol binario, la tarea es encontrar la distancia entre dos claves en un árbol binario, no se dan punteros principales. La distancia entre dos Nodes es el número mínimo de aristas a recorrer para llegar a un Node desde otro.
Ya hemos discutido un método que usa el árbol de segmentos para reducir el tiempo de consulta a O(logn), aquí la tarea es reducir el tiempo de consulta a O(1) al comprometer la complejidad del espacio a O(nlogn). En esta publicación, usaremos una tabla dispersa en lugar de un árbol de segmentos para encontrar el mínimo en un rango dado, que usa programación dinámica y manipulación de bits para lograr un tiempo de consulta O(1).
Una tabla dispersa preprocesará los valores mínimos del rango dado para la array L en el espacio Nlogn, es decir, cada Node contendrá una string de valores de longitud log(i) donde i es el índice del i-ésimo Node en la array L. Cada entrada en la tabla dispersa dice que M[i][j] representará el índice del valor mínimo en el subarreglo que comienza en i y tiene una longitud de 2^j.
La distancia entre dos Nodes se puede obtener en términos del ancestro común más bajo.
Dist(n1, n2) = Level[n1] + Level[n2] - 2*Level[lca]
Este problema se puede dividir en:
- Encontrar niveles de cada Node
- Encontrar el recorrido de Euler del árbol binario
- Construyendo una tabla dispersa para LCA.
Estos pasos se explican a continuación:
- Encuentre los niveles de cada Node aplicando un recorrido de orden de nivel .
- Encuentre el LCA de dos Nodes en un árbol binario en O (logn) almacenando el recorrido de Euler del árbol binario en una array y calculando otras dos arrays con la ayuda de los niveles de cada Node y el recorrido de Euler.
Estos pasos se muestran a continuación:
(I) Primero, encuentre Euler Tour of binary tree .
- (II) Luego, almacene los niveles de cada Node en la array de Euler.
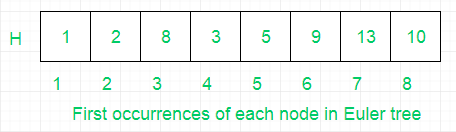
- (III) Luego, almacene las primeras ocurrencias de todos los Nodes del árbol binario en la array de Euler. H almacena los índices de los Nodes de la array de Euler, por lo que el rango de consulta para encontrar el mínimo se puede minimizar y optimizar aún más el tiempo de consulta.
- Luego construya una tabla dispersa en la array L y encuentre el valor mínimo, digamos X en el rango ( H[A] a H[B] ). Luego, usamos el índice del valor X como índice de la array de Euler para obtener LCA , es decir, Euler[índice(X)].
Sea A=8 y B=5.
(I) H[8]= 1 y H[5]=2
(II) obtenemos el valor mínimo en la array L entre 1 y 2 como X=0, índice=7
(III) Entonces, LCA= Euler[7], es decir, LCA=1.- Finalmente, aplique la fórmula de distancia discutida anteriormente para obtener la distancia entre dos Nodes.
C++
#include <bits/stdc++.h>
#define MAX 100001
using namespace std;
/* A tree node structure */
struct Node {
int data;
struct Node* left;
struct Node* right;
};
/* Utility function to create a new Binary Tree node */
struct Node* newNode(int data)
{
struct Node* temp = new struct Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Array to store level of each node
int level[MAX];
// Utility Function to store level of all nodes
void FindLevels(struct Node* root)
{
if (!root)
return;
// queue to hold tree node with level
queue<pair<struct Node*, int> > q;
// let root node be at level 0
q.push({ root, 0 });
pair<struct Node*, int> p;
// Do level Order Traversal of tree
while (!q.empty()) {
p = q.front();
q.pop();
// Node p.first is on level p.second
level[p.first->data] = p.second;
// If left child exits, put it in queue
// with current_level +1
if (p.first->left)
q.push({ p.first->left, p.second + 1 });
// If right child exists, put it in queue
// with current_level +1
if (p.first->right)
q.push({ p.first->right, p.second + 1 });
}
}
// Stores Euler Tour
int Euler[MAX];
// index in Euler array
int idx = 0;
// Find Euler Tour
void eulerTree(struct Node* root)
{
// store current node's data
Euler[++idx] = root->data;
// If left node exists
if (root->left) {
// traverse left subtree
eulerTree(root->left);
// store parent node's data
Euler[++idx] = root->data;
}
// If right node exists
if (root->right) {
// traverse right subtree
eulerTree(root->right);
// store parent node's data
Euler[++idx] = root->data;
}
}
// checks for visited nodes
int vis[MAX];
// Stores level of Euler Tour
int L[MAX];
// Stores indices of the first occurrence
// of nodes in Euler tour
int H[MAX];
// Preprocessing Euler Tour for finding LCA
void preprocessEuler(int size)
{
for (int i = 1; i <= size; i++) {
L[i] = level[Euler[i]];
// If node is not visited before
if (vis[Euler[i]] == 0) {
// Add to first occurrence
H[Euler[i]] = i;
// Mark it visited
vis[Euler[i]] = 1;
}
}
}
// Sparse table of size [MAX][LOGMAX]
// M[i][j] is the index of the minimum value in
// the sub array starting at i having length 2^j
int M[MAX][18];
// Utility function to preprocess Sparse table
void preprocessLCA(int N)
{
for (int i = 0; i < N; i++)
M[i][0] = i;
for (int j = 1; 1 << j <= N; j++)
for (int i = 0; i + (1 << j) - 1 < N; i++)
if (L[M[i][j - 1]] < L[M[i + (1 << (j - 1))][j - 1]])
M[i][j] = M[i][j - 1];
else
M[i][j] = M[i + (1 << (j - 1))][j - 1];
}
// Utility function to find the index of the minimum
// value in range a to b
int LCA(int a, int b)
{
// Subarray of length 2^j
int j = log2(b - a + 1);
if (L[M[a][j]] <= L[M[b - (1 << j) + 1][j]])
return M[a][j];
else
return M[b - (1 << j) + 1][j];
}
// Function to return distance between
// two nodes n1 and n2
int findDistance(int n1, int n2)
{
// Maintain original Values
int prevn1 = n1, prevn2 = n2;
// Get First Occurrence of n1
n1 = H[n1];
// Get First Occurrence of n2
n2 = H[n2];
// Swap if low>high
if (n2 < n1)
swap(n1, n2);
// Get position of minimum value
int lca = LCA(n1, n2);
// Extract value out of Euler tour
lca = Euler[lca];
// return calculated distance
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
void preProcessing(Node* root, int N)
{
// Build Tree
eulerTree(root);
// Store Levels
FindLevels(root);
// Find L and H array
preprocessEuler(2 * N - 1);
// Build sparse table
preprocessLCA(2 * N - 1);
}
/* Driver function to test above functions */
int main()
{
// Number of nodes
int N = 8;
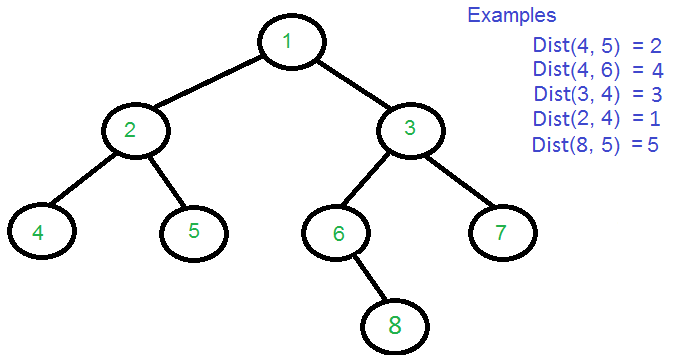
/* Constructing tree given in the above figure */
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
// Function to do all preprocessing
preProcessing(root, N);
cout << "Dist(4, 5) = " << findDistance(4, 5) << "\n";
cout << "Dist(4, 6) = " << findDistance(4, 6) << "\n";
cout << "Dist(3, 4) = " << findDistance(3, 4) << "\n";
cout << "Dist(2, 4) = " << findDistance(2, 4) << "\n";
cout << "Dist(8, 5) = " << findDistance(8, 5) << "\n";
return 0;
}
Java
// Java implementation of the approach
import java.util.*;
class GFG {
static class Pair<T, V> {
T first;
V second;
Pair() {
}
Pair(T first, V second) {
this.first = first;
this.second = second;
}
}
static class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
this.left = this.right = null;
}
}
static int MAX = 100001;
// Array to store level of each node
static int[] level = new int[MAX];
// Utility Function to store level of all nodes
static void FindLevels(Node root) {
if (root == null)
return;
// queue to hold tree node with level
Queue<Pair<Node, Integer>> q = new LinkedList<>();
// let root node be at level 0
q.add(new Pair<>(root, 0));
Pair<Node, Integer> p = new Pair<>();
// Do level Order Traversal of tree
while (!q.isEmpty()) {
p = q.poll();
// Node p.first is on level p.second
level[p.first.data] = p.second;
// If left child exits, put it in queue
// with current_level +1
if (p.first.left != null)
q.add(new Pair<>(p.first.left, p.second + 1));
// If right child exists, put it in queue
// with current_level +1
if (p.first.right != null)
q.add(new Pair<>(p.first.right, p.second + 1));
}
}
// Stores Euler Tour
static int[] Euler = new int[MAX];
// index in Euler array
static int idx = 0;
// Find Euler Tour
static void eulerTree(Node root) {
// store current node's data
Euler[++idx] = root.data;
// If left node exists
if (root.left != null) {
// traverse left subtree
eulerTree(root.left);
// store parent node's data
Euler[++idx] = root.data;
}
// If right node exists
if (root.right != null) {
// traverse right subtree
eulerTree(root.right);
// store parent node's data
Euler[++idx] = root.data;
}
}
// checks for visited nodes
static int[] vis = new int[MAX];
// Stores level of Euler Tour
static int[] L = new int[MAX];
// Stores indices of the first occurrence
// of nodes in Euler tour
static int[] H = new int[MAX];
// Preprocessing Euler Tour for finding LCA
static void preprocessEuler(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[Euler[i]];
// If node is not visited before
if (vis[Euler[i]] == 0) {
// Add to first occurrence
H[Euler[i]] = i;
// Mark it visited
vis[Euler[i]] = 1;
}
}
}
// Sparse table of size [MAX][LOGMAX]
// M[i][j] is the index of the minimum value in
// the sub array starting at i having length 2^j
static int[][] M = new int[MAX][18];
// Utility function to preprocess Sparse table
static void preprocessLCA(int N) {
for (int i = 0; i < N; i++)
M[i][0] = i;
for (int j = 1; 1 << j <= N; j++)
for (int i = 0; i + (1 << j) - 1 < N; i++)
if (L[M[i][j - 1]] < L[M[i + (1 << (j - 1))][j - 1]])
M[i][j] = M[i][j - 1];
else
M[i][j] = M[i + (1 << (j - 1))][j - 1];
}
// Utility function to find the index of the minimum
// value in range a to b
static int LCA(int a, int b) {
// Subarray of length 2^j
int j = (int) (Math.log(b - a + 1) / Math.log(2));
if (L[M[a][j]] <= L[M[b - (1 << j) + 1][j]])
return M[a][j];
else
return M[b - (1 << j) + 1][j];
}
// Function to return distance between
// two nodes n1 and n2
static int findDistance(int n1, int n2) {
// Maintain original Values
int prevn1 = n1, prevn2 = n2;
// Get First Occurrence of n1
n1 = H[n1];
// Get First Occurrence of n2
n2 = H[n2];
// Swap if low>high
if (n2 < n1) {
int temp = n1;
n1 = n2;
n2 = temp;
}
// Get position of minimum value
int lca = LCA(n1, n2);
// Extract value out of Euler tour
lca = Euler[lca];
// return calculated distance
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
static void preProcessing(Node root, int N) {
// Build Tree
eulerTree(root);
// Store Levels
FindLevels(root);
// Find L and H array
preprocessEuler(2 * N - 1);
// Build sparse table
preprocessLCA(2 * N - 1);
}
// Driver Code
public static void main(String[] args) {
// Number of nodes
int N = 8;
/* Constructing tree given in the above figure */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
// Function to do all preprocessing
preProcessing(root, N);
System.out.println("Dist(4, 5) = " + findDistance(4, 5));
System.out.println("Dist(4, 6) = " + findDistance(4, 6));
System.out.println("Dist(3, 4) = " + findDistance(3, 4));
System.out.println("Dist(2, 4) = " + findDistance(2, 4));
System.out.println("Dist(8, 5) = " + findDistance(8, 5));
}
}
// This code is contributed by
// sanjeev2552
Python3
from collections import deque
from math import log2
MAX = 100001
# A tree node structure
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Array to store level of each node
level = [0] * MAX
# Utility Function to store level of all nodes
def findLevels(root: Node):
global level
if root is None:
return
# queue to hold tree node with level
q = deque()
# let root node be at level 0
q.append((root, 0))
# Do level Order Traversal of tree
while q:
p = q[0]
q.popleft()
# Node p.first is on level p.second
level[p[0].data] = p[1]
# If left child exits, put it in queue
# with current_level +1
if p[0].left:
q.append((p[0].left, p[1] + 1))
# If right child exists, put it in queue
# with current_level +1
if p[0].right:
q.append((p[0].right, p[1] + 1))
# Stores Euler Tour
Euler = [0] * MAX
# index in Euler array
idx = 0
# Find Euler Tour
def eulerTree(root: Node):
global Euler, idx
idx += 1
# store current node's data
Euler[idx] = root.data
# If left node exists
if root.left:
# traverse left subtree
eulerTree(root.left)
idx += 1
# store parent node's data
Euler[idx] = root.data
# If right node exists
if root.right:
# traverse right subtree
eulerTree(root.right)
idx += 1
# store parent node's data
Euler[idx] = root.data
# checks for visited nodes
vis = [0] * MAX
# Stores level of Euler Tour
L = [0] * MAX
# Stores indices of the first occurrence
# of nodes in Euler tour
H = [0] * MAX
# Preprocessing Euler Tour for finding LCA
def preprocessEuler(size: int):
global L, H, vis
for i in range(1, size + 1):
L[i] = level[Euler[i]]
# If node is not visited before
if vis[Euler[i]] == 0:
# Add to first occurrence
H[Euler[i]] = i
# Mark it visited
vis[Euler[i]] = 1
# Sparse table of size [MAX][LOGMAX]
# M[i][j] is the index of the minimum value in
# the sub array starting at i having length 2^j
M = [[0 for i in range(18)] for j in range(MAX)]
# Utility function to preprocess Sparse table
def preprocessLCA(N: int):
global M
for i in range(N):
M[i][0] = i
j = 1
while 1 << j <= N:
i = 0
while i + (1 << j) - 1 < N:
if L[M[i][j - 1]] < L[M[i +
(1 << (j - 1))][j - 1]]:
M[i][j] = M[i][j - 1]
else:
M[i][j] = M[i + (1 << (j - 1))][j - 1]
i += 1
j += 1
# Utility function to find the index of the minimum
# value in range a to b
def LCA(a: int, b: int) -> int:
# Subarray of length 2^j
j = int(log2(b - a + 1))
if L[M[a][j]] <= L[M[b - (1 << j) + 1][j]]:
return M[a][j]
else:
return M[b - (1 << j) + 1][j]
# Function to return distance between
# two nodes n1 and n2
def findDistance(n1: int, n2: int) -> int:
# Maintain original Values
prevn1 = n1
prevn2 = n2
# Get First Occurrence of n1
n1 = H[n1]
# Get First Occurrence of n2
n2 = H[n2]
# Swap if low>high
if n2 < n1:
n1, n2 = n2, n1
# Get position of minimum value
lca = LCA(n1, n2)
# Extract value out of Euler tour
lca = Euler[lca]
# return calculated distance
return level[prevn1] + level[prevn2] - 2 * level[lca]
def preProcessing(root: Node, N: int):
# Build Tree
eulerTree(root)
# Store Levels
findLevels(root)
# Find L and H array
preprocessEuler(2 * N - 1)
# Build sparse table
preprocessLCA(2 * N - 1)
# Driver Code
if __name__ == "__main__":
# Number of nodes
N = 8
# Constructing tree given in the above figure
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
# Function to do all preprocessing
preProcessing(root, N)
print("Dist(4, 5) =", findDistance(4, 5))
print("Dist(4, 6) =", findDistance(4, 6))
print("Dist(3, 4) =", findDistance(3, 4))
print("Dist(2, 4) =", findDistance(2, 4))
print("Dist(8, 5) =", findDistance(8, 5))
# This code is contributed by
# sanjeev2552
C#
// C# implementation of the approach
using System;
using System.Collections.Generic;
public class GFG
{
public
class Pair<T, V>
{
public
T first;
public
V second;
public
Pair() {
}
public
Pair(T first, V second)
{
this.first = first;
this.second = second;
}
}
public
class Node
{
public
int data;
public
Node left, right;
public
Node(int data)
{
this.data = data;
this.left = this.right = null;
}
}
static int MAX = 100001;
// Array to store level of each node
static int[] level = new int[MAX];
// Utility Function to store level of all nodes
static void FindLevels(Node root)
{
if (root == null)
return;
// queue to hold tree node with level
Queue<Pair<Node, int>> q = new Queue<Pair<Node, int>>();
// let root node be at level 0
q.Enqueue(new Pair<Node,int>(root, 0));
Pair<Node, int> p = new Pair<Node,int>();
// Do level Order Traversal of tree
while (q.Count != 0)
{
p = q.Peek();
q.Dequeue();
// Node p.first is on level p.second
level[p.first.data] = p.second;
// If left child exits, put it in queue
// with current_level +1
if (p.first.left != null)
q.Enqueue(new Pair<Node,int>(p.first.left, p.second + 1));
// If right child exists, put it in queue
// with current_level +1
if (p.first.right != null)
q.Enqueue(new Pair<Node,int>(p.first.right, p.second + 1));
}
}
// Stores Euler Tour
static int[] Euler = new int[MAX];
// index in Euler array
static int idx = 0;
// Find Euler Tour
static void eulerTree(Node root)
{
// store current node's data
Euler[++idx] = root.data;
// If left node exists
if (root.left != null)
{
// traverse left subtree
eulerTree(root.left);
// store parent node's data
Euler[++idx] = root.data;
}
// If right node exists
if (root.right != null)
{
// traverse right subtree
eulerTree(root.right);
// store parent node's data
Euler[++idx] = root.data;
}
}
// checks for visited nodes
static int[] vis = new int[MAX];
// Stores level of Euler Tour
static int[] L = new int[MAX];
// Stores indices of the first occurrence
// of nodes in Euler tour
static int[] H = new int[MAX];
// Preprocessing Euler Tour for finding LCA
static void preprocessEuler(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[Euler[i]];
// If node is not visited before
if (vis[Euler[i]] == 0)
{
// Add to first occurrence
H[Euler[i]] = i;
// Mark it visited
vis[Euler[i]] = 1;
}
}
}
// Sparse table of size [MAX,LOGMAX]
// M[i,j] is the index of the minimum value in
// the sub array starting at i having length 2^j
static int[,] M = new int[MAX, 18];
// Utility function to preprocess Sparse table
static void preprocessLCA(int N)
{
for (int i = 0; i < N; i++)
M[i, 0] = i;
for (int j = 1; 1 << j <= N; j++)
for (int i = 0; i + (1 << j) - 1 < N; i++)
if (L[M[i, j - 1]] < L[M[i + (1 << (j - 1)), j - 1]])
M[i, j] = M[i, j - 1];
else
M[i, j] = M[i + (1 << (j - 1)), j - 1];
}
// Utility function to find the index of the minimum
// value in range a to b
static int LCA(int a, int b)
{
// Subarray of length 2^j
int j = (int) (Math.Log(b - a + 1) / Math.Log(2));
if (L[M[a,j]] <= L[M[b - (1 << j) + 1,j]])
return M[a,j];
else
return M[b - (1 << j) + 1,j];
}
// Function to return distance between
// two nodes n1 and n2
static int findDistance(int n1, int n2) {
// Maintain original Values
int prevn1 = n1, prevn2 = n2;
// Get First Occurrence of n1
n1 = H[n1];
// Get First Occurrence of n2
n2 = H[n2];
// Swap if low>high
if (n2 < n1)
{
int temp = n1;
n1 = n2;
n2 = temp;
}
// Get position of minimum value
int lca = LCA(n1, n2);
// Extract value out of Euler tour
lca = Euler[lca];
// return calculated distance
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
static void preProcessing(Node root, int N)
{
// Build Tree
eulerTree(root);
// Store Levels
FindLevels(root);
// Find L and H array
preprocessEuler(2 * N - 1);
// Build sparse table
preprocessLCA(2 * N - 1);
}
// Driver Code
public static void Main(String[] args)
{
// Number of nodes
int N = 8;
/* Constructing tree given in the above figure */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
// Function to do all preprocessing
preProcessing(root, N);
Console.WriteLine("Dist(4, 5) = " + findDistance(4, 5));
Console.WriteLine("Dist(4, 6) = " + findDistance(4, 6));
Console.WriteLine("Dist(3, 4) = " + findDistance(3, 4));
Console.WriteLine("Dist(2, 4) = " + findDistance(2, 4));
Console.WriteLine("Dist(8, 5) = " + findDistance(8, 5));
}
}
// This code is contributed by aashish1995
Javascript
<script>
// Javascript implementation of the approach
class Pair{
constructor(first, second)
{
this.first = first;
this.second = second;
}
}
class Node{
constructor(data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
var MAX = 100001;
// Array to store level of each node
var level = Array(MAX);
// Utility Function to store level of all nodes
function FindLevels(root)
{
if (root == null)
return;
// queue to hold tree node with level
var q = [];
// let root node be at level 0
q.push(new Pair(root, 0));
var p = new Pair();
// Do level Order Traversal of tree
while (q.length != 0)
{
p = q[0];
q.shift();
// Node p.first is on level p.second
level[p.first.data] = p.second;
// If left child exits, put it in queue
// with current_level +1
if (p.first.left != null)
q.push(new Pair(p.first.left, p.second + 1));
// If right child exists, put it in queue
// with current_level +1
if (p.first.right != null)
q.push(new Pair(p.first.right, p.second + 1));
}
}
// Stores Euler Tour
var Euler = Array(MAX);
// index in Euler array
var idx = 0;
// Find Euler Tour
function eulerTree(root)
{
// store current node's data
Euler[++idx] = root.data;
// If left node exists
if (root.left != null)
{
// traverse left subtree
eulerTree(root.left);
// store parent node's data
Euler[++idx] = root.data;
}
// If right node exists
if (root.right != null)
{
// traverse right subtree
eulerTree(root.right);
// store parent node's data
Euler[++idx] = root.data;
}
}
// checks for visited nodes
var vis = Array(MAX).fill(0);
// Stores level of Euler Tour
var L = Array(MAX).fill(0);
// Stores indices of the first occurrence
// of nodes in Euler tour
var H = Array(MAX).fill(0);
// Preprocessing Euler Tour for finding LCA
function preprocessEuler(size)
{
for (var i = 1; i <= size; i++)
{
L[i] = level[Euler[i]];
// If node is not visited before
if (vis[Euler[i]] == 0)
{
// Add to first occurrence
H[Euler[i]] = i;
// Mark it visited
vis[Euler[i]] = 1;
}
}
}
// Sparse table of size [MAX,LOGMAX]
// M[i,j] is the index of the minimum value in
// the sub array starting at i having length 2^j
var M = Array.from(Array(MAX), ()=>Array(18));
// Utility function to preprocess Sparse table
function preprocessLCA(N)
{
for (var i = 0; i < N; i++)
M[i][0] = i;
for (var j = 1; 1 << j <= N; j++)
for (var i = 0; i + (1 << j) - 1 < N; i++)
if (L[M[i][j - 1]] < L[M[i + (1 << (j - 1))][j - 1]])
M[i][j] = M[i][j - 1];
else
M[i][j] = M[i + (1 << (j - 1))][j - 1];
}
// Utility function to find the index of the minimum
// value in range a to b
function LCA(a, b)
{
// Subarray of length 2^j
var j = parseInt(Math.log(b - a + 1) / Math.log(2));
if (L[M[a][j]] <= L[M[b - (1 << j) + 1][j]])
return M[a][j];
else
return M[b - (1 << j) + 1][j];
}
// Function to return distance between
// two nodes n1 and n2
function findDistance( n1, n2)
{
// Maintain original Values
var prevn1 = n1, prevn2 = n2;
// Get First Occurrence of n1
n1 = H[n1];
// Get First Occurrence of n2
n2 = H[n2];
// Swap if low>high
if (n2 < n1)
{
var temp = n1;
n1 = n2;
n2 = temp;
}
// Get position of minimum value
var lca = LCA(n1, n2);
// Extract value out of Euler tour
lca = Euler[lca];
// return calculated distance
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
function preProcessing(root, N)
{
// Build Tree
eulerTree(root);
// Store Levels
FindLevels(root);
// Find L and H array
preprocessEuler(2 * N - 1);
// Build sparse table
preprocessLCA(2 * N - 1);
}
// Driver Code
// Number of nodes
var N = 8;
/* Constructing tree given in the above figure */
var root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
// Function to do all preprocessing
preProcessing(root, N);
document.write("Dist(4, 5) = " + findDistance(4, 5) + "<br>");
document.write("Dist(4, 6) = " + findDistance(4, 6) + "<br>");
document.write("Dist(3, 4) = " + findDistance(3, 4) + "<br>");
document.write("Dist(2, 4) = " + findDistance(2, 4) + "<br>");
document.write("Dist(8, 5) = " + findDistance(8, 5) + "<br>");
// This code is contributed by itsok.
</script>
Salida :
Dist(4, 5) = 2 Dist(4, 6) = 4 Dist(3, 4) = 3 Dist(2, 4) = 1 Dist(8, 5) = 5
Complejidad de tiempo : O(1)
Complejidad de espacio : O(N log N)
Publicación traducida automáticamente
Artículo escrito por Abhishek rajput y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA