Función booleana de conteo con algunas variables

Requisito previo: forma canónica y estándar
En los siguientes artículos, veremos algunas variedades de problemas con tres variables.

Declaración-1:
Contar el número de funciones booleanas posibles con dos variables de modo que haya exactamente dos términos mínimos.
Explicación:
Como ya sabemos que a partir de dos variables (a y b) $(2^2)$ se pueden formar cuatro números (0, 1, 2, 3), es decir, en dígitos binarios 00, 01, 10, 11 y los posibles términos Min son a’b’ , a’b, ab’, ab respectivamente, lo que da ‘1’ como salida para los respectivos dígitos binarios como entrada.

Por lo tanto, el número de funciones posibles con dos variables como entrada de modo que haya exactamente dos términos mínimos son,
```
 
```
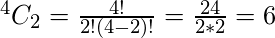
Donde ‘4’ es el número posible de dos variables y ‘2’ es el número deseado de términos mínimos para los que se necesita calcular el número de la función.
Declaración-2:
Contar el número de funciones booleanas posibles con tres variables de modo que haya exactamente tres términos mínimos.
Explicación:
Como ya sabemos que a partir de tres variables (a, b y c), $(2^3)$ se pueden formar 8 números (0, 1, 2, 3, 4, 5, 6, 7), es decir, en dígitos binarios 000, 001, 010 , 011, 100, 101, 110, 111 y los posibles términos Min son a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectivamente, lo que da ‘1 ‘ como salida para los respectivos dígitos binarios como entrada.

Por lo tanto, el número de funciones posibles con tres variables como entrada tales que hay exactamente tres términos mínimos son,
```
 
```
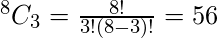
Donde ‘8’ es el número posible de tres variables y ‘3’ es el número deseado de términos mínimos para los que se necesita calcular el número de la función.
Declaración-3:
Contando el número de funciones booleanas posibles con tres variables tales que hay al menos 4 términos mínimos.
Explicación:
Como ya sabemos que a partir de tres variables (a, b y c) $(2^3)$ se pueden formar 8 números (0, 1, 2, 3, 4, 5, 6, 7), es decir, en dígitos binarios 000, 001, 010, 011, 100, 101, 110, 111 y los posibles términos mínimos son a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectivamente, lo que da ‘ 1’ como salida para los respectivos dígitos binarios como entrada.
Por lo tanto, el número de funciones posibles con tres variables como entrada de modo que haya como máximo 4 términos mínimos son,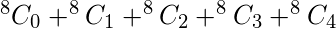
```
 
```
Donde ‘8’ es el número posible de tres variables y 0, 1, 2, 3, 4 son el número deseado de términos mínimos para los que se necesita calcular el número de la función.
Declaración-4:
Contar el número de funciones booleanas posibles con tres variables de modo que haya términos mínimos de 4 min.
Explicación:
Como ya sabemos que a partir de tres variables (a, b y c),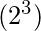 $(2^3)$ se pueden formar 8 números (0, 1, 2, 3, 4, 5, 6, 7), es decir, en dígitos binarios 000, 001, 010 , 011, 100, 101, 110, 111 y los posibles términos Min son a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectivamente, lo que da ‘1 ‘ como salida para los respectivos dígitos binarios como entrada.
Por lo tanto, el número de funciones posibles con tres variables como entrada de modo que haya un mínimo de 4 términos mínimos es,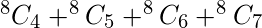
```
 
```
Donde ‘8’ es el número posible de tres variables y 4, 5, 6, 7 son el número deseado de términos mínimos para los que se necesita calcular el número de la función.
Declaración-5:
Contar el número de funciones booleanas posibles con variables ‘k’ de modo que haya términos mínimos ‘m’.
Explicación:
Como ya sabemos que a partir de ‘k’ variables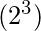 $(2^3)$ se pueden formar números.
Por lo tanto, el número de funciones posibles con variables ‘k’ como entrada, de modo que haya términos mínimos ‘m’ son,
```
 
```
Donde 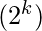$(2^k)$ es el número posible de las variables ‘k’ y ‘m’ es el número deseado de términos mínimos para los que se necesita calcular el número de la función.
Declaración-6:
Contando el número de funciones booleanas posibles en función neutral de ‘3’ variables donde hay igual número de términos mínimos y máximos.
Explicación:
Como ya sabemos que a partir de tres variables (a, b y c),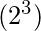 $(2^3)$ se pueden formar 8 números (0, 1, 2, 3, 4, 5, 6, 7), es decir, en dígitos binarios 000, 001, 010 , 011, 100, 101, 110, 111 y hay el mismo número de términos máximos y mínimos, lo que da ‘1’ como salida para los términos mínimos y ‘0’ como salida para los términos máximos para los respectivos dígitos binarios como entrada.

Por ejemplo, suponga que 000 son los dígitos binarios, entonces los términos mínimos serán a’b’c’ y los términos máximos serán abc.
Por lo tanto, el número de posibles funciones booleanas con tres variables en la función neutra son,
```
 
```
Donde ‘8’ es el número posible de tres variables y 4 es el número deseado de términos mínimos o máximos para los que se necesita calcular el número de la función.
Declaración-7:
Contar el número de funciones booleanas posibles en función neutral de variables ‘k’ donde hay un número igual de términos mínimos y máximos.
Explicación:
Como ya sabemos que a partir de ‘k’ variables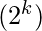 $(2^k)$ se pueden formar números.
Por lo tanto, el número de funciones booleanas posibles con variables ‘k’ como entrada donde hay un número igual de términos mínimos y máximos,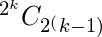
```
 
```
Donde 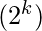$(2^k)$ es el número posible de las variables ‘k’ y 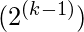$(2^{(k-1)})$ son el número deseado de términos mínimos o máximos para los que se necesita calcular el número de la función.

Publicación traducida automáticamente

Artículo escrito por Kanchan_Ray y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta