Cuente el número de pares de líneas que se cruzan en un punto

N líneas dadas tienen la forma a*x + b*y = c (a>0 o a==0 & b>0). Halla el número de pares de rectas que se cortan en un punto. Ejemplos:

Entrada: N=5 x + y = 2 x + y = 4 x = 1 x – y = 2 y = 3 Salida: 9 Entrada: N=2 x + 2y = 2 x + 2y = 4 Salida: 0

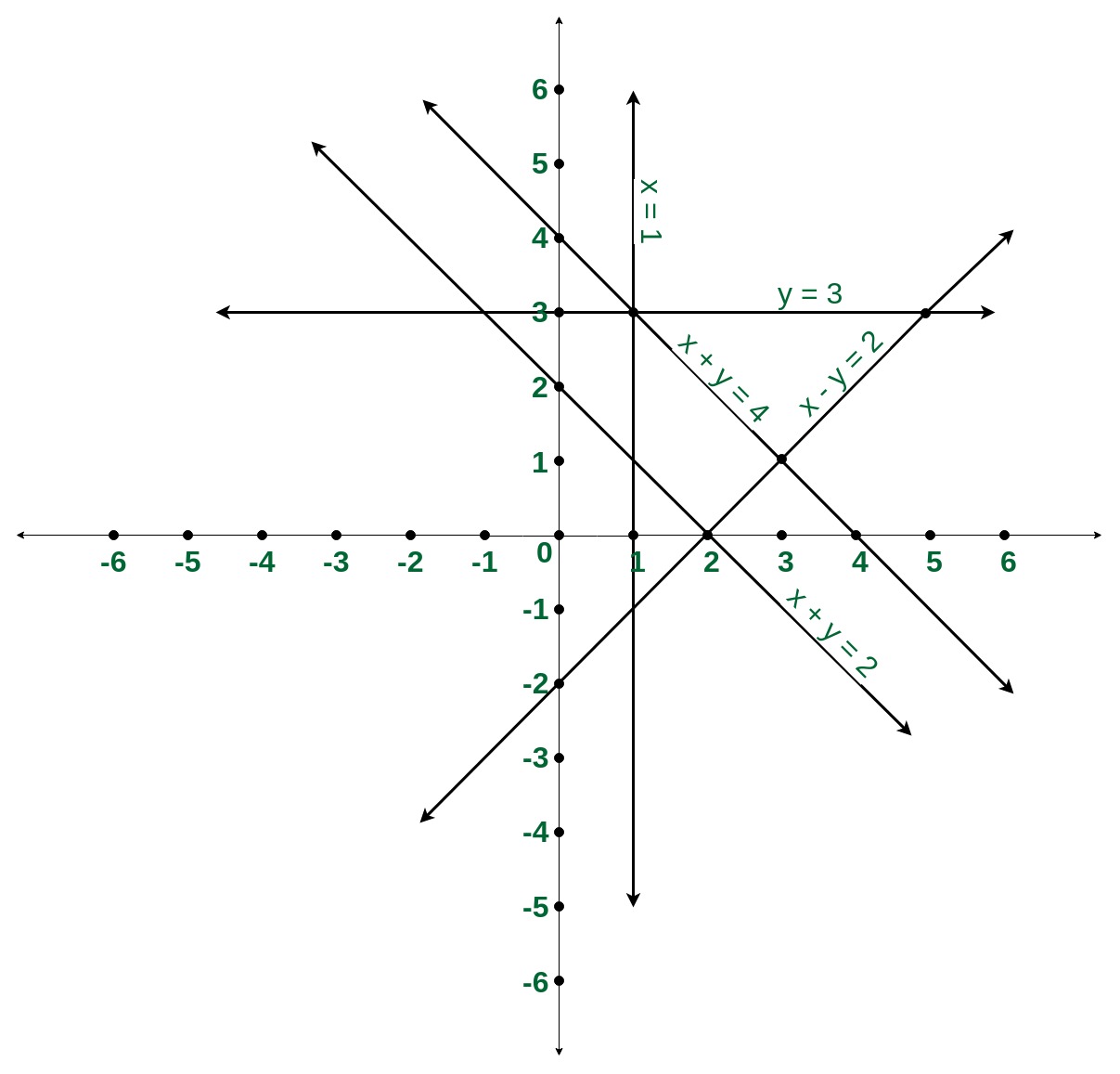
Acercarse: 

• Las líneas paralelas nunca se cruzan, por lo que se necesita un método para excluir líneas paralelas para cada línea.
• La pendiente de una línea se puede representar como un par (a, b). Construya un mapa con clave como pendiente y valor como un conjunto con c como entradas para que tenga una cuenta de las líneas paralelas.
• Itere sobre las líneas, agréguelas al mapa y mantenga una variable Tot que cuente el número total de líneas hasta ahora.
• Ahora, para cada línea, actualice la variable Tot , luego agregue Tot a la respuesta y reste el número de líneas paralelas a esa línea, incluyéndose a sí misma.

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation to calculate
// pair of intersecting lines
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the number
// of intersecting pair of lines
void numberOfPairs(int a[],int b[],int c[],int N){
 
    int count = 0, Tot = 0;
 
    // Construct a map of slope and
    // corresponding c value
    map<pair<int, int>, set<int> > LineMap;
 
    // iterate over each line
    for (int i = 0; i < N; i++) {
 
        // Slope can be represented
        // as pair(a, b)
        pair<int, int> Slope =
                    make_pair(a[i], b[i]);
 
        // Checking if the line does
        // not already exist
        if (!LineMap[Slope].count(c[i])){
            // maintaining a count
            // of total lines
            Tot++;
            LineMap[Slope].insert(c[i]);
 
            // subtracting the count of
            // parallel lines including itself
            count += Tot -
                    LineMap[Slope].size();
        }
    }
 
    cout << count << endl;
}
 
// Driver code
int main()
{
    // A line can be represented as ax+by=c
    // such that (a>0 || (a==0 & b>0) )
    // a and b are already in there lowest
    // form i.e gcd(a, b)=1
    int N = 5;
    int a[] = { 1, 1, 1, 1, 0 };
    int b[] = { 1, 1, 0, -1, 1 };
    int c[] = { 2, 4, 1, 2, 3 };
     
    numberOfPairs(a,b,c,N);
 
    return 0;
}

// JavaScript implementation to calculate
// pair of intersecting lines
 
// Function to return the number
// of intersecting pair of lines
function numberOfPairs(a, b, c, N){
 
    let count = 0;
    let Tot = 0;
 
    // Construct a map of slope and
    // corresponding c value
    let LineMap = new Map();
    // map<pair<int, int>, set<int> > LineMap;
 
    // iterate over each line
    for (let i = 0; i < N; i++) {
 
        // Slope can be represented
        // as pair(a, b)
        let Slope = [a[i], b[i]].join();
 
        // Checking if the line does
        // not already exist
        if (!LineMap.has(Slope) || !LineMap.get(Slope).has(c[i])){
            // maintaining a count
            // of total lines
            Tot = Tot + 1;
            if(!LineMap.has(Slope))
                LineMap.set(Slope, new Set().add(c[i]));
            else
                LineMap.set(Slope, LineMap.get(Slope).add(c[i]));
 
            // subtracting the count of
            // parallel lines including itself
            count = count +  Tot - LineMap.get(Slope).size;
        }
    }
 
    console.log(count);
}
 
// Driver code
// A line can be represented as ax+by=c
// such that (a>0 || (a==0 & b>0) )
// a and b are already in there lowest
// form i.e gcd(a, b)=1
let N = 5;
let a = [1, 1, 1, 1, 0];
let b = [1, 1, 0, -1, 1];
let c = [2, 4, 1, 2, 3 ];
 
numberOfPairs(a,b,c,N);
 
// The code is contributed by Gatuam goel (gautamgoel962)

9

Complejidad del tiempo: 

Complejidad espacial : O (N) desde que se usa un mapa