Dada una array de enteros positivos (puede contener duplicados) y un número ‘m’, encuentre el número de tripletes desordenados ((A i , A j , Ak ) y (A j , A i , Ak ) y otras permutaciones son contados como uno solo) con producto igual a ‘m’.
Ejemplos:
Entrada: arr[] = { 1, 4, 6, 2, 3, 8}, M = 24
Salida: 3
Los tripletes son {1, 4, 6} {1, 3, 8} {4, 2, 3}Entrada: arr[] = { 0, 4, 6, 2, 3, 8}, M = 18
Salida: 0
No hay tripletes en este caso
Una solución con O(N 2 ) ha sido discutida en la publicación anterior . En esta publicación se ha discutido un mejor enfoque con menor complejidad.
Enfoque: Se sigue el siguiente algoritmo para resolver el problema anterior.
- Use un mapa hash para contar la frecuencia de cada elemento en la array dada.
- Declare un conjunto que pueda almacenar trillizos, de modo que solo se tomen en cuenta los trillizos desordenados.
- Iterar de 1 a sqrt(m) en un ciclo (deje que la variable sea i), ya que el número máximo por el cual M es divisible es sqrt(M) omitiendo M.
- Verifique si M es divisible por i o no y si i está presente en la array de enteros o no, si lo está, luego vuelva a hacer un bucle de 1 a M/i (deje que la variable de bucle sea j).
- Nuevamente, verifique si M es divisible por j o no y si j está presente en la array de enteros o no, si es así, verifique si el número restante que es ((M / i) / j) está presente o no.
- Si está presente, entonces se ha formado un triplete. Para evitar trillizos duplicados, insértelos en el conjunto en orden ordenado.
- Verifique si el tamaño del conjunto aumenta después de la inserción del triplete, si lo hace, luego use la combinatoria para encontrar el número de tripletes.
- Para encontrar el número de trillizos, se cumplirán las siguientes condiciones.
- Si todos los A i , A j y A k son únicos, entonces el número de combinaciones será el producto de sus frecuencias.
- Si todos son iguales, entonces solo podemos elegir tres de ellos, por lo tanto, la fórmula se encuentra en
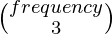 .
. - Si cualquiera de los dos es igual (sean Ai y Aj), el conteo será
![Rendered by QuickLaTeX.com frequency[Ai] \choose 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2b0dad5d13cee469cf62e2bf9172550_l3.png) * frecuencia[A k ]
* frecuencia[A k ]
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to find the
// number of triplets in array
// whose product is equal to M
#include <bits/stdc++.h>
using namespace std;
// Function to count the triplets
int countTriplets(int a[], int m, int n)
{
// hash-map to store the frequency of every number
unordered_map<int, int> frequency;
// set to store the unique triplets
set<pair<int, pair<int, int> > > st;
// count the number of times
// every element appears in a map
for (int i = 0; i < n; i++) {
frequency[a[i]] += 1;
}
// stores the answer
int ans = 0;
// iterate till sqrt(m) since tnum2t is the
// maximum number tnum2t can divide M except itself
for (int i = 1; i * i <= m; i++) {
// if divisible and present
if (m % i == 0 and frequency[i]) {
// remaining number after division
int num1 = m / i;
// iterate for the second number of the triplet
for (int j = 1; j * j <= num1; j++) {
// if divisible and present
if (num1 % j == 0 and frequency[j]) {
// remaining number after division
int num2 = num1 / j;
// if the third number is present in array
if (frequency[num2]) {
// a temp array to store the triplet
int temp[] = { num2, i, j };
// sort the triplets
sort(temp, temp + 3);
// get the size of set
int setsize = st.size();
// insert the triplet in ascending order
st.insert({ temp[0], { temp[1], temp[2] } });
// if the set size increases after insertion,
// it means a new triplet is found
if (setsize != st.size()) {
// if all the number in triplets are unique
if (i != j and j != num2)
ans += frequency[i] * frequency[j] * frequency[num2];
// if Ai and Aj are same among triplets
else if (i == j && j != num2)
ans += (frequency[i] * (frequency[i] - 1) / 2)
* frequency[num2];
// if Aj and Ak are same among triplets
else if (j == num2 && j != i)
ans += (frequency[j] * (frequency[j] - 1) / 2)
* frequency[i];
// if three of them are
// same among triplets
else if (i == j and j == num2)
ans += (frequency[i] * (frequency[i] - 1) * (frequency[i] - 2) / 6);
// if Ai and Ak are same among triplets
else
ans += (frequency[i] * (frequency[i] - 1) / 2)
* frequency[j];
}
}
}
}
}
}
return ans;
}
// Driver Code
int main()
{
int a[] = { 1, 4, 6, 2, 3, 8 };
int m = 24;
int n = sizeof(a) / sizeof(a[0]);
cout << countTriplets(a, m, n);
return 0;
}
Java
// Java program to find the
// number of triplets in array
// whose product is equal to M
import java.util.*;
class GFG
{
// Function to count the triplets
static int countTriplets(int a[], int m, int n)
{
// hash-map to store
// the frequency of every number
HashMap<Integer, Integer> frequency
= new HashMap<>();
// put to store the unique triplets
Set<String> st = new HashSet<String>();
// count the number of times
// every element appears in a map
for (int i = 0; i < n; i++)
{
frequency.put(a[i],(frequency.get(a[i]) ==
null ? 1:(frequency.get(a[i]) + 1)));
}
// stores the answer
int ans = 0;
// iterate till sqrt(m) since tnum2t is the
// maximum number tnum2t can divide M except itself
for (int i = 1; i * i <= m; i++)
{
// if divisible && present
if (m % i == 0 && frequency.get(i)!=null)
{
// remaining number after division
int num1 = m / i;
// iterate for the second number of the triplet
for (int j = 1; j * j <= num1; j++)
{
// if divisible && present
if (num1 % j == 0 && frequency.get(j) != null)
{
// remaining number after division
int num2 = num1 / j;
// if the third number is present in array
if (frequency.get(num2) != null)
{
// a temp array to store the triplet
int temp[] = { num2, i, j };
// sort the triplets
Arrays.sort(temp);
// get the size of put
int setsize = st.size();
// add the triplet in ascending order
st.add(temp[0]+" "+ temp[1]+" " +temp[2] );
// if the put size increases after addition,
// it means a new triplet is found
if (setsize != st.size())
{
// if all the number in triplets are unique
if (i != j && j != num2)
ans += frequency.get(i) *
frequency.get(j) *
frequency.get(num2);
// if Ai && Aj are same among triplets
else if (i == j && j != num2)
ans += (frequency.get(i) *
(frequency.get(i) - 1) / 2)
* frequency.get(num2);
// if Aj && Ak are same among triplets
else if (j == num2 && j != i)
ans += (frequency.get(j) *
(frequency.get(j) - 1) / 2)
* frequency.get(i);
// if three of them are
// same among triplets
else if (i == j && j == num2)
ans += (frequency.get(i) *
(frequency.get(i) - 1) *
(frequency.get(i) - 2) / 6);
// if Ai && Ak are same among triplets
else
ans += (frequency.get(i) *
(frequency.get(i) - 1) / 2)
* frequency.get(j);
}
}
}
}
}
}
return ans;
}
// Driver Code
public static void main(String args[])
{
int a[] = { 1, 4, 6, 2, 3, 8 };
int m = 24;
int n = a.length;
System.out.println(countTriplets(a, m, n));
}
}
// This code is contributed by Arnab Kundu
Python3
# Python3 program to find the
# number of triplets in array
# whose product is equal to M
import math
# Function to count the triplets
def countTriplets(a, m, n):
# hash-map to store
# the frequency of every number
frequency = {}
# put to store the unique triplets
st = set({})
# count the number of times
# every element appears in a map
for i in range(n):
if a[i] in frequency:
frequency[a[i]] += 1
else:
frequency[a[i]] = 1
# stores the answer
ans = 0
# iterate till sqrt(m) since tnum2t is the
# maximum number tnum2t can divide M except itself
i = 1
while i * i <= m:
# if divisible && present
if (m % i == 0 and i in frequency):
# remaining number after division
num1 = int(m / i)
# iterate for the second number of the triplet
j = 1
while j * j <= num1:
# if divisible && present
if (num1 % j == 0 and j in frequency):
# remaining number after division
num2 = math.floor(num1 / j)
# if the third number is present in array
if num2 in frequency:
# a temp array to store the triplet
temp = [ num2, i, j ]
# sort the triplets
temp.sort()
# get the size of put
setsize = len(st)
# add the triplet in ascending order
st.add(str(temp[0])+" "+ str(temp[1])+" " +str(temp[2]))
# if the put size increases after addition,
# it means a new triplet is found
if setsize != len(st):
# if all the number in
# triplets are unique
if (i != j and j != num2):
ans += frequency[i] * frequency[j] * frequency[num2]
# if Ai && Aj are same among triplets
elif (i == j and j != num2):
ans += (frequency[i] * (frequency[i] - 1) / 2) * frequency[num2]
# if Aj && Ak are same among triplets
elif (j == num2 and j != i):
ans += (frequency[j] * (frequency[j] - 1) / 2) * frequency[i]
# if three of them are
# same among triplets
elif (i == j and j == num2):
ans += (frequency[i] * (frequency[i] - 1) * (frequency[i] - 2) / 6)
# if Ai && Ak are same among triplets
else:
ans += (frequency[i] * (frequency[i] - 1) / 2) * frequency[j]
j += 1
i += 1
return int(ans)
a=[1, 4, 6, 2, 3, 8 ]
m = 24;
n = len(a)
print(countTriplets(a, m, n))
# This code is contributed by rameshtravel07.
C#
// C# program to find the
// number of triplets in array
// whose product is equal to M
using System;
using System.Collections.Generic;
class GFG {
// Function to count the triplets
static int countTriplets(int[] a, int m, int n)
{
// hash-map to store
// the frequency of every number
Dictionary<int, int> frequency = new Dictionary<int, int>();
// put to store the unique triplets
HashSet<string> st = new HashSet<string>();
// count the number of times
// every element appears in a map
for (int i = 0; i < n; i++)
{
if(frequency.ContainsKey(a[i]))
{
frequency[a[i]] += 1;
}
else{
frequency[a[i]] = 1;
}
}
// stores the answer
int ans = 0;
// iterate till sqrt(m) since tnum2t is the
// maximum number tnum2t can divide M except itself
for (int i = 1; i * i <= m; i++)
{
// if divisible && present
if (m % i == 0 && frequency.ContainsKey(i))
{
// remaining number after division
int num1 = m / i;
// iterate for the second number of the triplet
for (int j = 1; j * j <= num1; j++)
{
// if divisible && present
if (num1 % j == 0 && frequency.ContainsKey(j))
{
// remaining number after division
int num2 = num1 / j;
// if the third number is present in array
if (frequency.ContainsKey(num2))
{
// a temp array to store the triplet
int[] temp = { num2, i, j };
// sort the triplets
Array.Sort(temp);
// get the size of put
int setsize = st.Count;
// add the triplet in ascending order
st.Add(temp[0].ToString()+" "+ temp[1].ToString()+" " +temp[2].ToString());
// if the put size increases after addition,
// it means a new triplet is found
if (setsize != st.Count)
{
// if all the number in triplets are unique
if (i != j && j != num2)
ans += frequency[i] *
frequency[j] *
frequency[num2];
// if Ai && Aj are same among triplets
else if (i == j && j != num2)
ans += (frequency[i] *
(frequency[i] - 1) / 2)
* frequency[num2];
// if Aj && Ak are same among triplets
else if (j == num2 && j != i)
ans += (frequency[j] *
(frequency[j] - 1) / 2)
* frequency[i];
// if three of them are
// same among triplets
else if (i == j && j == num2)
ans += (frequency[i] *
(frequency[i] - 1) *
(frequency[i] - 2) / 6);
// if Ai && Ak are same among triplets
else
ans += (frequency[i] *
(frequency[i] - 1) / 2)
* frequency[j];
}
}
}
}
}
}
return ans;
}
// Driver code
static void Main() {
int[] a = { 1, 4, 6, 2, 3, 8 };
int m = 24;
int n = a.Length;
Console.Write(countTriplets(a, m, n));
}
}
// This code is contributed by decode2207.
Javascript
<script>
// JavaScript program to find the
// number of triplets in array
// whose product is equal to M
// Function to count the triplets
function countTriplets(a,m,n)
{
// hash-map to store
// the frequency of every number
let frequency = new Map();
// put to store the unique triplets
let st = new Set();
// count the number of times
// every element appears in a map
for (let i = 0; i < n; i++)
{
frequency.set(a[i],(frequency.get(a[i]) ==
null ? 1:(frequency.get(a[i]) + 1)));
}
// stores the answer
let ans = 0;
// iterate till sqrt(m) since tnum2t is the
// maximum number tnum2t can divide M except itself
for (let i = 1; i * i <= m; i++)
{
// if divisible && present
if (m % i == 0 && frequency.get(i)!=null)
{
// remaining number after division
let num1 = m / i;
// iterate for the second number of the triplet
for (let j = 1; j * j <= num1; j++)
{
// if divisible && present
if (num1 % j == 0 && frequency.get(j) != null)
{
// remaining number after division
let num2 = Math.floor(num1 / j);
// if the third number is present in array
if (frequency.get(num2) != null)
{
// a temp array to store the triplet
let temp = [ num2, i, j ];
// sort the triplets
temp.sort(function(a,b){return a-b;});
// get the size of put
let setsize = st.size;
// add the triplet in ascending order
st.add(temp[0]+" "+ temp[1]+" " +temp[2] );
// if the put size increases after addition,
// it means a new triplet is found
if (setsize != st.size)
{
// if all the number in
// triplets are unique
if (i != j && j != num2)
ans += frequency.get(i) *
frequency.get(j) *
frequency.get(num2);
// if Ai && Aj are same among triplets
else if (i == j && j != num2)
ans += (frequency.get(i) *
(frequency.get(i) - 1) / 2)
* frequency.get(num2);
// if Aj && Ak are same among triplets
else if (j == num2 && j != i)
ans += (frequency.get(j) *
(frequency.get(j) - 1) / 2)
* frequency.get(i);
// if three of them are
// same among triplets
else if (i == j && j == num2)
ans += (frequency.get(i) *
(frequency.get(i) - 1) *
(frequency.get(i) - 2) / 6);
// if Ai && Ak are same among triplets
else
ans += (frequency.get(i) *
(frequency.get(i) - 1) / 2)
* frequency.get(j);
}
}
}
}
}
}
return ans;
}
// Driver Code
let a=[1, 4, 6, 2, 3, 8 ];
let m = 24;
let n = a.length;
document.write(countTriplets(a, m, n));
// This code is contributed by avanitrachhadiya2155
</script>
3
Complejidad de tiempo: O(N * log N)