Conversión de forma cuadrática a forma canónica en MATLAB

La forma cuadrática es un polinomio homogéneo de segundo grado en cualquier número de variables. En este artículo veremos, Conversión de la Forma Cuadrática a la Forma Canónica.

Por ejemplo, 

si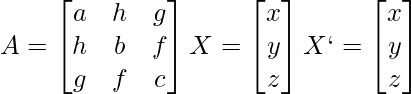  

Entonces,  , Que es una forma cuadrática.

Toda forma cuadrática se puede reducir a una suma de cuadrados, llamada forma canónica:

λ1x2 + λ2y2 + λ3z2, 
Where λ1, λ2 & λ3 are Eigen Values of the above 
Matrix 'A' (Matrix of Quadratic form)

Pasos para convertir forma cuadrática a forma canónica:

Paso 1: Considere que la forma cuadrática dada tiene el siguiente formato:

ax2+by2+cz2+2fyz+2gxz+2hxy

Paso 2:  Luego, de la forma cuadrática anterior, encontramos la siguiente array ‘A’ (llamada array de forma cuadrática):

Paso 3:  Después de encontrar la array «A» anterior, encontramos los valores propios de la misma resolviendo su ecuación característica. La Ecuación Característica de ‘A’ es:

|A-λI3| = 0, 
Where I3 is the Identity Matrix of order 3.

Paso 4:  Expandiendo la relación anterior, obtenemos:

λ3 + C1λ2 + C2λ + C3I3 = 0, 
where C1, C2 & C3 are Real Constants.

Paso 5:  Resolviendo la relación anterior, obtenemos 3 soluciones para ‘λ’, sean las 3 soluciones λ ₁ , λ ₂ y λ _3.

Paso 6: Luego, la forma canónica de la forma cuadrática dada (ax ² +by ² +cz ² +2fyz+2gxz+2hxy) se representa como:

Canonical Form = λ1x2 + λ2y2 + λ3z2

Los diferentes parámetros asociados con la forma cuadrática son:

• Índice: Es el Número de Autovalores Positivos de la Array ‘A’ (Array de forma Cuadrática). El índice de la forma cuadrática también se puede definir como el número de términos cuadrados positivos en la representación de la forma canónica de la forma cuadrática.
• Firma: Es la diferencia entre el Número de Autovalores Positivos y Negativos de la Array ‘A’ (Array de forma Cuadrática). La firma de la forma cuadrática también se puede definir como la diferencia entre el número de términos cuadrados positivos y negativos en la representación de la forma canónica de la forma cuadrática.
• Rango: Es el número de Autovalores distintos de cero de la Array ‘A’ (Array de forma Cuadrática). El rango de la forma cuadrática también se puede definir como un número de filas distintas de cero en la forma escalonada de filas de la array ‘A’.
• Naturaleza de la forma cuadrática: Con base en la naturaleza de los valores propios de la array ‘A’ (array de forma cuadrática), se decide la naturaleza de la forma cuadrática.
  • Si todos los valores propios de la array ‘A’ (array de forma cuadrática) son positivos, entonces se dice que la naturaleza de la forma cuadrática es positiva definida.
  • De lo contrario, si todos los valores propios de la array ‘A’ (array de forma cuadrática) son negativos, entonces se dice que la naturaleza de la forma cuadrática es definida negativa.
  • De lo contrario, si todos los valores propios de la array ‘A’ (array de forma cuadrática) no son negativos, entonces se dice que la naturaleza de la forma cuadrática es semidefinida positiva.
  • De lo contrario, si todos los valores propios de la array ‘A’ (array de forma cuadrática) son no positivos, entonces se dice que la naturaleza de la forma cuadrática es semidefinida negativa.
  • De lo contrario, en todos los demás casos (mezcla de valores propios positivos, negativos y cero de ‘A’), se dice que la naturaleza de la forma cuadrática es «indefinida».

Nota: Aquí, un valor propio no negativo significa que puede ser cero o una válvula positiva. Además, un valor propio no positivo significa que puede ser cero o una válvula negativa.

Las funciones de MATLAB utilizadas en el siguiente código son:

• disp(“txt”): este método muestra el mensaje-“txt” al usuario.
• entrada («txt»): este método muestra el mensaje-«txt» y espera a que el usuario ingrese un valor y presione la tecla Retorno.
• eig(A): este método devuelve un vector columna que contiene los valores propios de la array cuadrada ‘A’.
• strcat(A, B,…): Este método concatena horizontalmente el texto en sus argumentos de entrada.
• rank(A): Este método devuelve el rango de la array ‘A’. 

Ejemplo:

% MATLAB Implementation to convert Quadratic Form
% to Canonical Form and to find Different Parameters
% associated with Quadratic form:
 clear all 
 clc        
 disp("MATLAB Implementation to convert Quadratic Form to
     Canonical Form and to find Different Parameters associated
     with Quadratic form | GeeksforGeeks")
E = input("Enter the coefficients in the order 
   [a,b,c,f,g,h] for the Quadratic form: [ax^2+by^2+cz^2+2fyz+2gxz+2hxy] : ");
a = E(1);
b = E(2); 
c = E(3);
  
% Coefficients of the Quadratic form
f = E(4); g=E(5); h=E(6);  
  
% Finding Matrix 'A' (Matrix of Quadratic form) 
e = eig(A);
A = [a h g;h b f;g f c];  
  
% λ1 , λ2 & λ3
l1 = e(1);
l2 = e(2);
l3 = e(3); 
  
disp(strcat('The Canonical form of given Quadratic form is: 
(',num2str(l1),')x^2+(',num2str(l2),')y^2+(',num2str(l3),')z^2'))
a=0;
b=0;
  
% Counting the Number of Positive and Negative Eigen 
% values of Matrix 'A' (Matrix of Quadratic form) 
for i=1:3    
    if(e(i)>0)
        a=a+1;
    elseif(e(i)<0)
        b=b+1;
    end
end
  
% Number of Positive Eigen values of Matrix 
% 'A' (Matrix of Quadratic form) 
index=a
  
% Difference between the number of Positive and Negative 
% Eigen values of Matrix 'A' (Matrix of Quadratic form) 
  
signature=a-b  
rank=rank(A)
 % If all Eigen values of Matrix 'A'
 % (Matrix of Quadratic form) are Positive
   
if(a==3)           
    disp('The Nature of given Quadratic form is Positive Definite')
% If all Eigen values of Matrix 'A' 
% (Matrix of Quadratic form) are Negative
  
elseif(b==3)       
    disp('The Nature of given Quadratic form is Negative Definite')
% If all Eigen values of Matrix 'A' (Matrix of Quadratic form) 
% are non-negative (positive or zero)
  
elseif(b==0)        
    disp('The Nature of given Quadratic form is Positive Semi-Definite')
% If all Eigen values of Matrix 'A' (Matrix of Quadratic
% form) are non-positive (negative or zero)
  
elseif(a==0)        
    disp('The Nature of given Quadratic form is Negative Semi-Definite')
else                
% If all Eigen values of Matrix 'A' (Matrix of 
% Quadratic form) are Mix of Positive, Negative & Zero
  
    disp('The Nature of given Quadratic form is InDefinite')
end

input: If the Quadratic form is x2+3y2+3z2-2yz

Producción:

 

Input: If the Quadratic form is 2yz+2xz-2xy

Producción: