Dado un árbol binario , la tarea es convertir el árbol binario dado en el árbol simétrico agregando el número mínimo de Nodes en el árbol dado.
Ejemplos:
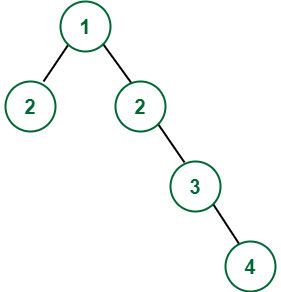
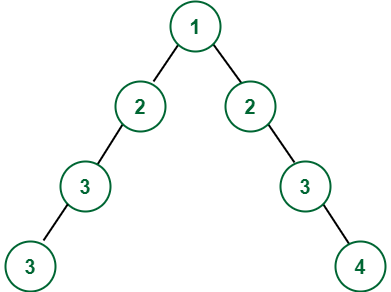
Aporte:
Producción:
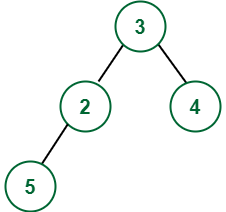
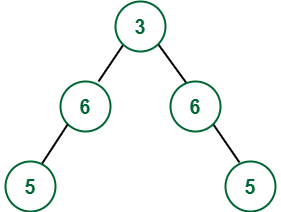
Aporte:
Producción:
Enfoque: Para resolver este problema, siga los pasos a continuación:
- Cree una función buildSymmetricTree que acepte dos parámetros root1 y root2 .
- Aquí, root1 y root2 son los Nodes que están en lugares simétricos entre sí.
- Entonces, inicialmente, tanto root1 como root2 contendrán el valor de la raíz y en cada llamada recursiva:
- Si root1 existe pero root2 no, cree un nuevo Node con el mismo valor que root1 y colóquelo en la posición de root2 .
- Siga el paso anterior también para root1 si root2 existe pero root1 no.
- Si el valor de root1 y root2 no es el mismo, cambie el valor de ambos Nodes a la suma de ellos.
- Ahora, realice las siguientes dos llamadas recursivas para las posiciones simétricas en (raíz1->izquierda, raíz2->derecha) y (raíz1->derecha, raíz2->izquierda).
- El árbol se volverá simétrico después de que se realicen todas las llamadas recursivas.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Node
class Node {
public:
int val;
Node *left, *right;
Node(int val)
{
this->val = val;
left = right = NULL;
}
};
// Function to convert the given tree
// into a symmetric
Node* buidSymmetricTree(Node* root1,
Node* root2)
{
// Base Case
if (root1 == NULL and root2 == NULL) {
return NULL;
}
// If root1 == NULL & root2 != NULL
if (root1 == NULL) {
// Create new node for root2
// and attaching it to tree
Node* node = new Node(root2->val);
root1 = node;
}
// If root2 == NULL and root1 != NULL
if (root2 == NULL) {
// Create new node for root1
// and attaching it to tree
Node* node = new Node(root1->val);
root2 = node;
}
// If both nodes are different
// then change both nodes values
// to the sum of them
if (root1->val != root2->val) {
int temp = root1->val + root2->val;
root1->val = temp;
root2->val = temp;
}
// Recurring to the left
root1->left
= buidSymmetricTree(
root1->left, root2->right);
// Recurring to the right
root1->right
= buidSymmetricTree(
root1->right, root2->left);
// Return root pointer
return root1;
}
// Function to perform the Inorder
// Traversal of the tree
void inorder(Node* root)
{
// Base Case
if (root == NULL)
return;
inorder(root->left);
cout << root->val << " ";
inorder(root->right);
}
// Driver Code
int main()
{
Node* root = new Node(3);
root->left = new Node(2);
root->right = new Node(4);
root->left->left = new Node(5);
// Function to make the given
// tree symmetric
buidSymmetericTree(root, root);
// Print the inorder traversal
inorder(root);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
class GFG{
// Node
static class Node {
int val;
Node left, right;
Node(int val)
{
this.val = val;
left = right = null;
}
};
// Function to convert the given tree
// into a symmetric
static Node buidSymmetricTree(Node root1,
Node root2)
{
// Base Case
if (root1 == null && root2 == null) {
return null;
}
// If root1 == null & root2 != null
if (root1 == null) {
// Create new node for root2
// and attaching it to tree
Node node = new Node(root2.val);
root1 = node;
}
// If root2 == null and root1 != null
if (root2 == null) {
// Create new node for root1
// and attaching it to tree
Node node = new Node(root1.val);
root2 = node;
}
// If both nodes are different
// then change both nodes values
// to the sum of them
if (root1.val != root2.val) {
int temp = root1.val + root2.val;
root1.val = temp;
root2.val = temp;
}
// Recurring to the left
root1.left
= buidSymmetricTree(
root1.left, root2.right);
// Recurring to the right
root1.right
= buidSymmetricTree(
root1.right, root2.left);
// Return root pointer
return root1;
}
// Function to perform the Inorder
// Traversal of the tree
static void inorder(Node root)
{
// Base Case
if (root == null)
return;
inorder(root.left);
System.out.print(root.val+ " ");
inorder(root.right);
}
// Driver Code
public static void main(String[] args)
{
Node root = new Node(3);
root.left = new Node(2);
root.right = new Node(4);
root.left.left = new Node(5);
// Function to make the given
// tree symmetric
buidSymmetericTree(root, root);
// Print the inorder traversal
inorder(root);
}
}
// This code is contributed by umadevi9616
Python3
# Python Program to implement # the above approach # Node class Node: def __init__(self, val): self.val = val self.left = self.right = None # Function to convert the given tree # into a symmetric def buidSymmetricTree(root1, root2): # Base Case if (root1 == None and root2 == None): return None # If root1 == null & root2 != null if (root1 == None): # Create new node for root2 # and attaching it to tree node = Node(root2.val) root1 = node # If root2 == null and root1 != null if (root2 == None): # Create new node for root1 # and attaching it to tree node = Node(root1.val) root2 = node # If both nodes are different # then change both nodes values # to the sum of them if (root1.val != root2.val): temp = root1.val + root2.val root1.val = temp root2.val = temp # Recurring to the left root1.left = buidSymmetricTree( root1.left, root2.right) # Recurring to the right root1.right = buidSymmetricTree(root1.right, root2.left) # Return root pointer return root1 # Function to perform the Inorder # Traversal of the tree def inorder(root): # Base Case if (root == None): return inorder(root.left) print(root.val, end=" ") inorder(root.right) # Driver Code root = Node(3) root.left = Node(2) root.right = Node(4) root.left.left = Node(5) # Function to make the given # tree symmetric buidSymmetericTree(root, root) # Print the inorder traversal inorder(root) # This code is contributed by gfgking.
C#
// C# program for the above approach
using System;
public class GFG {
// Node
public class Node {
public int val;
public Node left, right;
public Node(int val) {
this.val = val;
left = right = null;
}
};
// Function to convert the given tree
// into a symmetric
static Node buidSymmetricTree(Node root1, Node root2)
{
// Base Case
if (root1 == null && root2 == null) {
return null;
}
// If root1 == null & root2 != null
if (root1 == null) {
// Create new node for root2
// and attaching it to tree
Node node = new Node(root2.val);
root1 = node;
}
// If root2 == null and root1 != null
if (root2 == null) {
// Create new node for root1
// and attaching it to tree
Node node = new Node(root1.val);
root2 = node;
}
// If both nodes are different
// then change both nodes values
// to the sum of them
if (root1.val != root2.val) {
int temp = root1.val + root2.val;
root1.val = temp;
root2.val = temp;
}
// Recurring to the left
root1.left = buidSymmetricTree(root1.left, root2.right);
// Recurring to the right
root1.right = buidSymmetricTree(root1.right, root2.left);
// Return root pointer
return root1;
}
// Function to perform the Inorder
// Traversal of the tree
static void inorder(Node root)
{
// Base Case
if (root == null)
return;
inorder(root.left);
Console.Write(root.val + " ");
inorder(root.right);
}
// Driver Code
public static void Main(String[] args) {
Node root = new Node(3);
root.left = new Node(2);
root.right = new Node(4);
root.left.left = new Node(5);
// Function to make the given
// tree symmetric
buidSymmetericTree(root, root);
// Print the inorder traversal
inorder(root);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// JavaScript Program to implement
// the above approach
// Node
class Node {
constructor(val) {
this.val = val;
this.left = this.right = null;
}
};
// Function to convert the given tree
// into a symmetric
function buidSymmetricTree(root1,
root2) {
// Base Case
if (root1 == null && root2 == null) {
return null;
}
// If root1 == null & root2 != null
if (root1 == null) {
// Create new node for root2
// and attaching it to tree
let node = new Node(root2.val);
root1 = node;
}
// If root2 == null and root1 != null
if (root2 == null) {
// Create new node for root1
// and attaching it to tree
let node = new Node(root1.val);
root2 = node;
}
// If both nodes are different
// then change both nodes values
// to the sum of them
if (root1.val != root2.val) {
let temp = root1.val + root2.val;
root1.val = temp;
root2.val = temp;
}
// Recurring to the left
root1.left
= buidSymmetricTree(
root1.left, root2.right);
// Recurring to the right
root1.right
= buidSymmetricTree(
root1.right, root2.left);
// Return root pointer
return root1;
}
// Function to perform the Inorder
// Traversal of the tree
function inorder(root) {
// Base Case
if (root == null)
return;
inorder(root.left);
document.write(root.val + " ");
inorder(root.right);
}
// Driver Code
let root = new Node(3);
root.left = new Node(2);
root.right = new Node(4);
root.left.left = new Node(5);
// Function to make the given
// tree symmetric
buidSymmetericTree(root, root);
// Print the inorder traversal
inorder(root);
// This code is contributed by Potta Lokesh
</script>
Producción:
5 6 3 6 5
Complejidad temporal: O(N)
Espacio auxiliar: O(1)