Convierta la array de covarianza en array de correlación usando Python

En este artículo, discutiremos la relación entre la covarianza y la correlación y programaremos nuestra propia función para calcular la covarianza y la correlación usando python. 

Covarianza: 

Nos dice cómo se relacionan dos cantidades entre sí, digamos que queremos calcular la covarianza entre x e y, entonces el resultado puede ser uno de estos.

where 

are the means of x and y respectively. 

Interpretando la salida:  

La covarianza entre x e y es: 

Covarianza(x,y) > 0 : esto significa que están relacionados positivamente 

Covarianza(x,y) < 0 : esto significa que x e y están relacionados negativamente 

si Covarianza(x,y) = 0 : entonces x e y son independientes entre sí.

Array de covarianza: 

La covarianza proporciona una medida de la fuerza de la correlación entre dos variables o más conjuntos de variables, para calcular la array de covarianza, se usa el método cov() en numpy .  

Sintaxis:  

ny.cov( m, y=Ninguno, rowvar=Verdadero, bias=Falso, ddof=Ninguno, fweights=Ninguno, aweights=Ninguno )

m : [array_like] Una variable 1D o 2D. las variables son columnas

y : [array_like] Tiene la misma forma que la de m.

rowvar: [bool, opcional] Si rowvar es True (predeterminado), cada fila representa una variable, con observaciones en las columnas. De lo contrario, la relación se transpone:

sesgo: la normalización predeterminada es falsa. Si el sesgo es Verdadero, normaliza los puntos de datos.

ddof: si no es Ninguno, se anula el valor predeterminado implícito por el sesgo. Tenga en cuenta que ddof=1 devolverá la estimación imparcial, incluso si se especifican tanto fweights como aweights.

fweights : fweight es una array 1-D de pesos de frecuencia enteros

aweights : aweight es una array 1-D de pesos de vectores de observación.

Devoluciones: Devuelve array de covarianza ndarray 

Correlación:

Muestra si los pares de variables están relacionados entre sí y con qué fuerza. La correlación toma valores entre -1 y +1, donde los valores cercanos a +1 representan una fuerte correlación positiva y los valores cercanos a -1 representan una fuerte correlación negativa. Da la dirección y la fuerza de la relación entre las variables.

Array de correlación:

Es básicamente una array de covarianza. También conocida como array de autocovarianza, array de dispersión, array de varianza o array de varianza-covarianza. Es una array en la que la posición ij define la correlación entre el i ^-ésimo y el j ^-ésimo parámetro del conjunto de datos dado. Se calcula utilizando el método numpy ‘s corcoeff() .  

Sintaxis: 

 numpy.corrcoef( x, y=Ninguno, rowvar=Verdadero, bias=<sin valor>, ddof=<sin valor> )

x :  Una array 1-D o 2-D que contiene múltiples variables y observaciones. Cada fila de x representa una variable y cada columna una sola observación de todas esas variables. Consulte también rowvar a continuación.

y , opcional: un conjunto adicional de variables y observaciones. y tiene la misma forma que x.

rowvar : si rowvar es True (predeterminado), cada fila representa una variable, con observaciones en las columnas. De lo contrario, la relación se transpone: cada columna representa una variable, mientras que las filas contienen observaciones.

Devoluciones: ndarray

Entonces, ¿por qué necesitamos correlación? 

1. La covarianza nos dice si dos variables aleatorias están relacionadas con +ve o -ve, no nos dice por cuánto.
2. La covarianza es variante de los cambios aritméticos, por ejemplo: si multiplicamos x por 10 o dividimos por 10, el resultado cambiará, esto no es cierto para la correlación donde los resultados permanecen sin cambios por tales operaciones.
3. La salida de la covarianza es difícil de comparar, ya que los valores pueden oscilar entre – infinito y + infinito. Mientras que los valores de salida de la correlación oscilan entre 0 y 1.

Relación entre correlación y covarianza 

La correlación es solo covarianza normalizada, consulte la fórmula a continuación.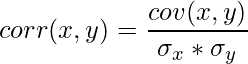 

donde 

son la desviación estándar de x e y respectivamente. 

Programa Python para convertir array de covarianza a array de correlación 

Para resolver este problema, hemos seleccionado los datos del iris porque para calcular la covarianza necesitamos datos y es mejor si usamos un conjunto de datos de ejemplo de palabras reales. 

Cargar y mostrar el conjunto de datos 

import numpy as np
import pandas as pd
 
# loading in the iris dataset for demo purposes
 
dataset = pd.read_csv("iris.csv")
 
dataset.head()

En este ejemplo, no usaremos la columna de destino 

data = dataset.iloc[:, :-1].values

Programa para implementar array de covarianza:  

# calculates the covariance between x and y
def calcCov(x, y):
 
    mean_x, mean_y = x.mean(), y.mean()
    n = len(x)
 
    return sum((x - mean_x) * (y - mean_y)) / n
 
 
# calculates the Covariance matrix
def covMat(data):
 
    # get the rows and cols
    rows, cols = data.shape
 
    # the covariance matroix has a shape of n_features x n_features
    # n_featurs  = cols - 1 (not including the target column)
    cov_mat = np.zeros((cols, cols))
 
    for i in range(cols):
 
        for j in range(cols):
            # store the value in the matrix
            cov_mat[i][j] = calcCov(data[:, i], data[:, j])
 
    return cov_mat
 
  covMat(data)

Salida : 

Salida numpy cov() : 

np.cov(data,rowvar=False)

 
nota: el rowVars debe hacerse falso; de lo contrario, tomará las filas como características, columnas y observaciones. 

Salida :  

Cálculo de correlación: 

En esta función, vamos a convertir la array de Covarianza a correlación. 

# Now calculating Correlation using our Covariance function (covMat())
 
 
def corrMat(data):
 
    rows, cols = data.shape
 
    corr_mat = np.zeros((cols, cols))
 
    for i in range(cols):
 
        for j in range(cols):
 
            x, y = data[:, i], data[:, j]
            # not here that we are just normalizing the covariance matrix
            corr_mat[i][j] = calcCov(x, y) / (x.std() * y.std())
 
    return corr_mat
  corrMat(data)
   
  

Producción: 

El corrcoef() en numpy también se puede usar para calcular la correlación. 

np.corrcoef(data,rowvar=False)

Producción: