La corrección de Bessel se refiere a la parte n-1 utilizada como denominador en la fórmula de varianza muestral o distribución muestral.
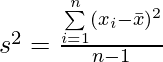
¿Por qué n-1?
Suponga que se extraen n observaciones independientes de una población con media(u) y varianza(sigma
2
). En general, tanto (u) como (sigma) son desconocidos y deben estimarse.
La media muestral estima la media poblacional(u) y la varianza muestral s 2 estima la varianza poblacional (sigma 2 ). Idealmente (sigma 2 ) debería estimarse con
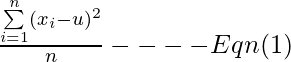
Dado que u no se conoce, la media muestral resulta ser el mejor estimador que se puede usar. Por eso
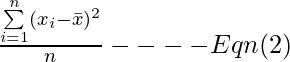
Problema:
al restar la media de la muestra en la ecuación (2), la suma es lo más pequeña posible; aproximadamente, la media de la muestra debe estar cerca del centro de las observaciones, mientras que la media de la población puede tener cualquier valor. Entonces, la suma en Eqn(2) va a ser más pequeña que la suma en Eqn(1) , por lo tanto, E qn(2) tiende a subestimar el verdadero valor de la varianza de la población.
Solución:
para compensar eso, dividir por n-1 hace que la varianza de la muestra sea un poco más grande de lo que sería si se dividiera por n. Resulta que matemáticamente compensa correctamente el problema.
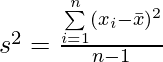
En promedio, este estimador es igual a la varianza de la población (sigma 2 ), no es obvio aquí por qué aquí (n-1) funciona, ¿por qué este estimador en promedio es igual a la varianza de la población (sigma 2 )? ¿Por qué (n-2) o (n-3) o (n-0.5) no se usa para la división?
Cuando la desviación estándar de la muestra se calcula a partir de una muestra de n valores, se utiliza la media de la muestra que ya se ha calculado a partir de esa misma muestra de n valores. La media muestral calculada ya ha «agotado» uno de los » grados de libertad de variabilidad» (que es la media misma) que está disponible en la muestra. Solo quedan n-1 grados de libertad de variabilidad para el cálculo de la desviación estándar de la muestra.
Ejemplo:
supongamos que se extraen 3 observaciones independientes de una población en la que se desconoce la media de la población (u), encontramos que la media de la muestra = 5 y la usamos para estimar la media de la población (u). Dada esta información, las dos primeras observaciones pueden ser cualquier cosa , suponga que son 7 y 5.
| i | x yo | x i -(muestra_media) |
|---|---|---|
| 1. | 7 | 7-5=2 |
| 2. | 5 | 5-5=0 |
| 3. | 3 | 3-5=-2 |
Si la media de la observación es 5 y sabemos que las dos primeras observaciones son 7 y 5, entonces la tercera debe ser 3 y sabemos que esta tercera desviación debe ser -2, ya que todas las desviaciones de la media de la muestra siempre suman cero .
Entonces, la tercera observación ya no puede tener ningún valor, así que aquí solo quedan dos grados de libertad una vez que se conocen la media de la muestra y cualquiera de estos tres valores, sabemos cuál debe ser el tercer valor, comenzamos con tres grados de libertad cuando teníamos tres observaciones independientes de la población pero perdimos un grado de libertad cuando estimamos la media poblacional(u) con la media muestral. Por lo tanto, para calcular la(s) varianza(s) muestral(es ) aquí, tomamos la suma de las desviaciones al cuadrado y la dividimos por los grados de libertad (3-1).
Entonces, al estimar la varianza de la población, generalmente se divide por los grados de libertad en lugar del tamaño de la muestra, ya que esto da como resultado un mejor estimador.