Clases laterales en Matemáticas

Coset es un subconjunto de un grupo matemático que consta de todos los productos obtenidos al multiplicar el elemento fijo del grupo por cada uno de los elementos del subgrupo dado, ya sea a la derecha o a la izquierda. Los mCosets son una herramienta básica en el estudio de grupos.

Supongamos que si Aes un grupo y Bes un subgrupo de A, y es un elemento de A, entonces

aB = {ab : b an element of B } is left coset of B in A,

La clase lateral izquierda de Bin Aes un subconjunto de Ade forma aBpara algunos a(elemento de A). En aB(coset izquierdo), aes representativo del coset.

y

Ba = {ba : b an element of B } is right coset of B in A.

La clase lateral derecha de Bin Aes un subconjunto de Ade forma Bapara algunos a(elemento de A). En la clase lateral derecha Ba, ase hace referencia al elemento como representante de la clase lateral.

El mapa aB -> (aB)' = Ba'map define la biyección entre las clases laterales izquierdas y Blas clases laterales derechas, por lo que el total de las clases laterales izquierdas es equivalente al total de las clases laterales derechas. El valor común se llama índice de Bin A.

Las clases laterales izquierda y derecha son siempre las mismas en el caso de agrupaciones abelianas. La notación utilizada cambia a a+Bo B+asi la operación de grupo se escribe de forma aditiva.

Definición utilizando clases de equivalencia:
algunos autores definen las clases laterales izquierdas de Bin Acomo clases de equivalencia dadas por x ~ yuna relación de equivalencia inferior Asi y solo si se da un x'ysubconjunto de B. La relación también se puede describir x ~ ysi y solo si xb = yse describe Bcon certeza b. Se puede ver que la relación dada es simplemente una relación de equivalencia y que dos conceptos son idénticos. En consecuencia, dos cosets izquierdos Bson Aequivalentes o disjuntos. Por lo tanto, cada elemento de Apertenece a la clase lateral izquierda única y, por lo tanto, las clases laterales izquierdas forman la partición de A. También son válidas afirmaciones similares para clases laterales correctas.

Clases laterales dobles:
si Aes un grupo By Cson subgrupos de A, entonces en clases laterales Adobles By Cson conjuntos de BaC= { bac: bun elemento de B, cun elemento de B}. Estas son las clases laterales izquierda Cy derecha de B, respectivamente, si B=1 y C=1.

Notación:
Suponga Aque es grupo y By C.son subgrupos de A.

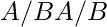• denota un conjunto de cosetsof izquierdos Ben A.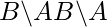
• denota 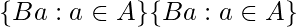un conjunto de clases laterales derechas de Bin A.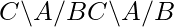
• denota 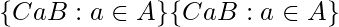un conjunto de dobles clases laterales de By Cen A.

Aplicaciones:

1. En la teoría de grupos computacional, las clases laterales son esenciales.
2. Cosets juegan un papel clave en el teorema de Lagrange.
3. El algoritmo de Thistlethwaite utilizado para resolver el cubo de Rubik se basa en gran medida en clases laterales.
4. la corrección de errores lineales en los datos decodificados obtenidos se realiza utilizando clases laterales.
5. Se utilizan para construir conjuntos Vitali, una especie de paquete no medible.