El diagrama de caja es un gráfico estadístico que ayuda en la visualización de datos. Se utiliza para mostrar la distribución de datos numéricos utilizando varios cuartiles. Son los siguientes:
- Extremo inferior: es el valor mínimo en el conjunto de datos que se encuentra al final del bigote.
- Primer cuartil: también se conoce como cuartil inferior, donde el 25 % de las puntuaciones se encuentran por debajo de él.
- Mediana: Es básicamente el punto medio que divide la caja en dos mitades iguales. También se le conoce como Segundo Cuartil.
- Tercer cuartil: también se conoce como cuartil superior en el que el 25% de los datos está por encima y el 75% restante cae por debajo.
- Rango intercuartílico: muestra la parte media del diagrama de caja, que es el 50% de las puntuaciones. Se abrevia como IQR .
- Extremo superior: es el valor máximo en el conjunto de datos que se encuentra al final del bigote.
- Bigote: Los dos bigotes en la parte superior e inferior básicamente indican el valor fuera del rango IQR o el 50% de las puntuaciones.
- Valores atípicos: los puntos en el diagrama de caja que se encuentran fuera de los bigotes.
Algunos enlaces importantes para obtener más información sobre diagramas de caja:
- diagrama de caja
- Diagrama de caja usando Python
- Diagrama de caja en R
- ¿Qué es el diagrama de caja y la condición de los valores atípicos?
- Comprender diferentes diagramas de caja con visualización
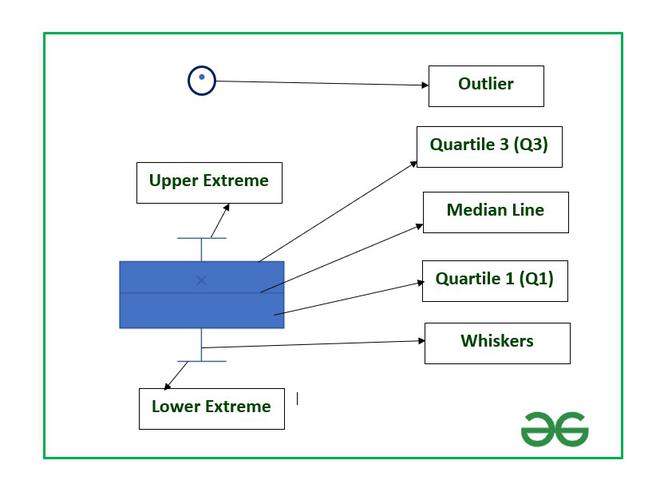
Estructura del diagrama de caja
En este artículo, veremos cómo crear diagramas de caja y también cómo encontrar los parámetros importantes asociados con los diagramas de caja en Excel usando un ejemplo adecuado.
Ejemplo: Considere el IMC de diez estudiantes de la sección A-1 y el de la sección A-2. IMC significa Índice de Masa Corporal, que es un parámetro importante para juzgar la grasa corporal y la salud de una persona en función de la altura y el peso de una persona.

Los pasos para crear un diagrama de caja:
- Inserte los datos en las celdas como se muestra arriba.
- Seleccione los datos y vaya a la pestaña Insertar en la parte superior de la ventana de Excel.
- Ahora haga clic en el menú Gráfico estadístico . Aparecerá un menú desplegable.
- Ahora seleccione el gráfico de cajas y bigotes .

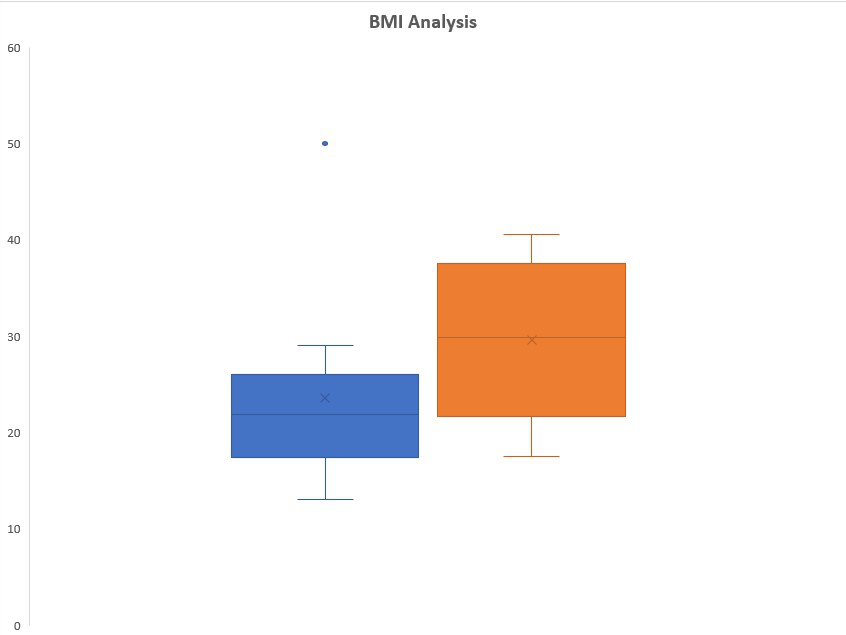
diagrama de caja
El diagrama de caja por defecto será exclusivo del valor medio. Para que sea inclusivo de la media:
- Seleccione el diagrama de caja.
- Haga clic con el botón derecho y seleccione Formato de serie de datos.
- En el cuadro de diálogo Formato de serie de datos, marque «Media inclusiva» en Cálculo de cuartiles.

Para dar formato a un diagrama de caja, use el símbolo + en la esquina superior derecha del gráfico, como se muestra a continuación:

Marque la opción Etiquetas de datos para agregar etiquetas de datos en los gráficos de caja y hacer que el gráfico sea más revelador.

Puede examinar los valores de las etiquetas de datos usando la siguiente sección donde vamos a discutir cómo calcular estos parámetros usando fórmulas de Excel.
Fórmula para calcular los parámetros asociados al diagrama de caja:
Para calcular los diferentes valores del cuartil utilice la fórmula:
= QUARTILE.INC(Cell_Range, integer)
Aquí,
- Rango de celdas: Rango de celdas. En nuestro caso es de A2 a A11 para el tramo A-1 y de B2 a B11 para el tramo A-2
- entero : [0,4]
| Valores de cuartiles | Fórmula |
|---|---|
| extremo inferior | =CUARTIL.INC(Rango_Celdas, 0) |
| Q1 | =CUARTIL.INC(Rango_Celda, 1) |
| Mediana | =CUARTIL.INC(Rango_Celdas, 2) |
| Q3 | =CUARTIL.INC(Rango_Celdas, 3) |
| extremo superior | =CUARTIL.INC(Rango_Celdas, 4) |
Haz una tabla de ayuda en Excel para calcular las fórmulas anteriores. La tabla auxiliar se puede usar para interpretar nuestro diagrama de caja y los valores.
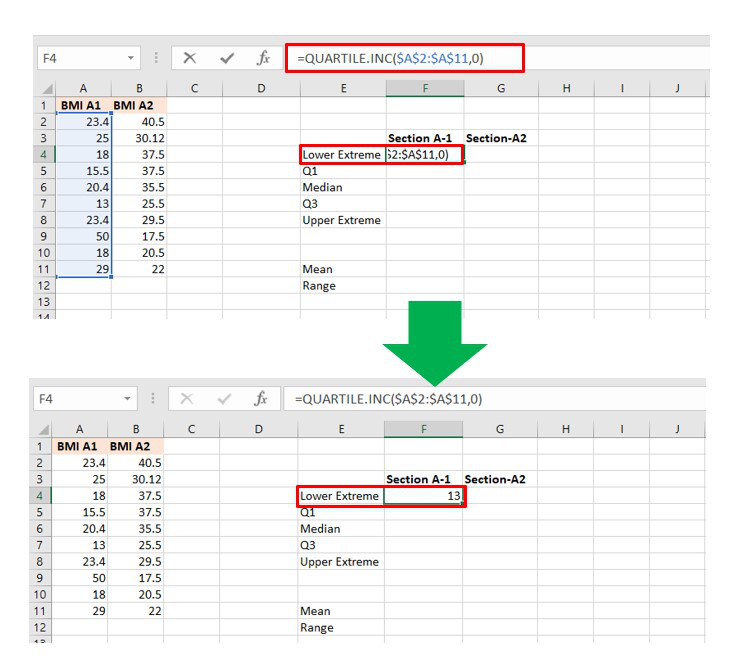
Cálculo del límite inferior
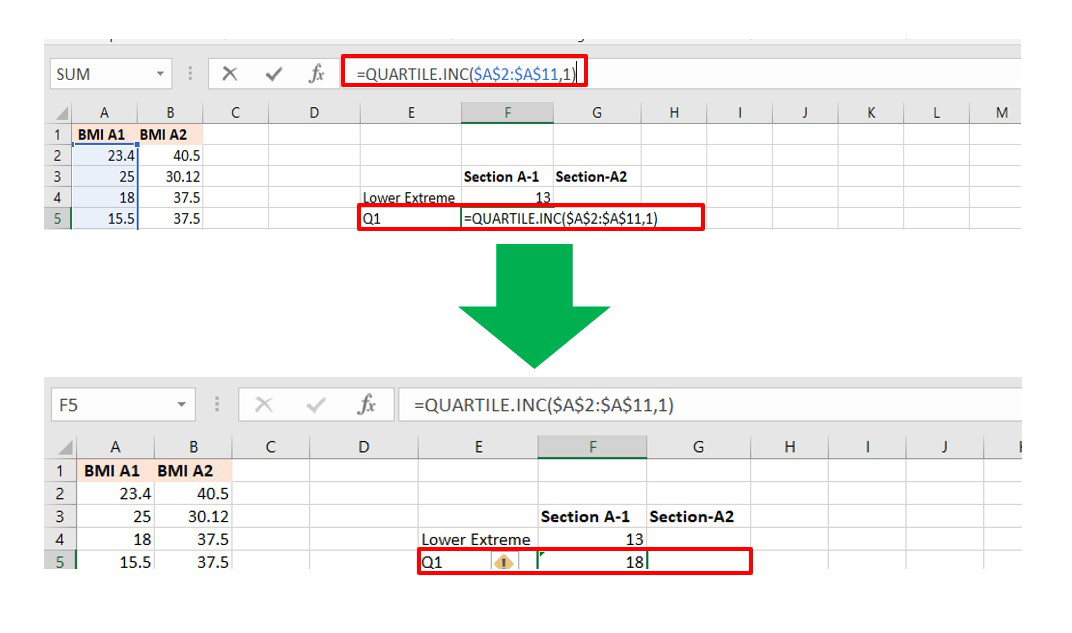
Cálculo del cuartil 1
Del mismo modo, puede calcular todos los demás parámetros para ambas secciones. La mesa final se verá así:

Algunos otros parámetros importantes en un diagrama de caja son (1) Media (2) Rango. Las fórmulas son:
= AVERAGE(Cell_Range) = (Upper Extreme - Lower Extreme)


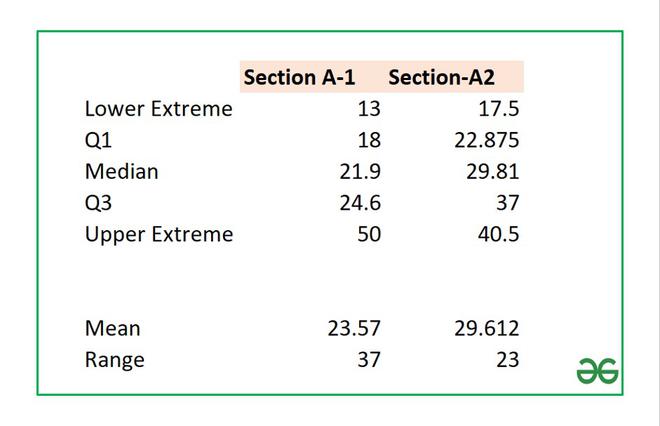
Mesa auxiliar
Otro parámetro importante en un diagrama de caja es un valor atípico que depende del valor del rango intercuartílico (IQR) . La fórmula para el IQR es:
IQR = Quartile_3 - Quartile_1
En nuestro ejemplo, el valor de IQR es 6,6, que puede calcular a partir de la tabla auxiliar. Ahora, un punto es un valor atípico si el valor es:
below (Quartile_1 - IQR*1.5) and above (Quartile_3 + IQR*1.5)
En el ejemplo dado para la sección A-1, tenemos un valor atípico en el valor 50, que es el valor máximo del IMC. Después del cálculo, el valor será:
IQR * 1.5=9.9 Q3 + IQR * 1.5 = 34.5 Since, 50 > 34.5 so it is in the outlier of the box plot.
De manera similar, puede calcular los parámetros anteriores para el segundo diagrama de caja y puede observar que los cinco parámetros están dentro del rango y, por lo tanto, no hay valores atípicos.
Para eliminar el valor atípico en Box plot-1, debe modificar el valor máximo de 50 a cualquier valor menor o igual a 34.5.
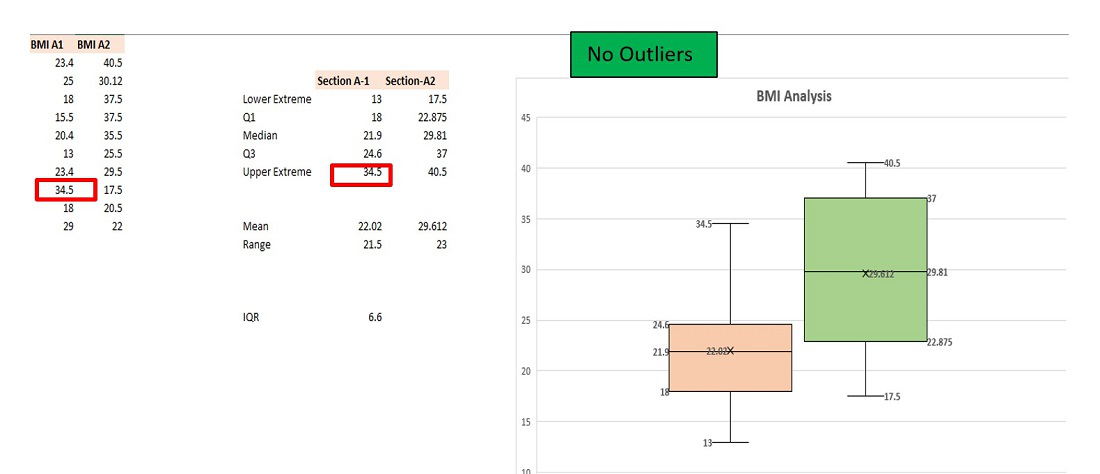
Valor atípico eliminado
Publicación traducida automáticamente
Artículo escrito por rishabhchakrabortygfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA