Requisitos previos: árbol binario a lista doblemente enlazada
Dado un árbol binario , la tarea es crear un árbol binario equilibrado a partir de todos los Nodes de hoja del árbol binario dado.
Ejemplos:
Input:
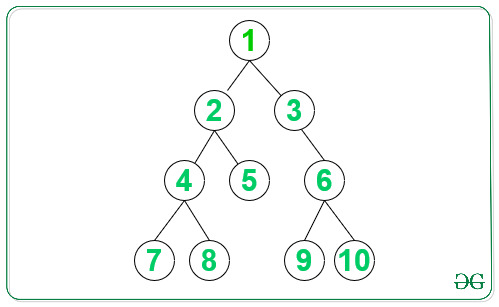
Output: 7 8 5 9 10 Explanation: Required balanced binary tree will be:
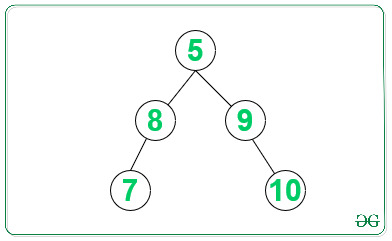
Input:

Output: 13 21 29 7 15
Explanation: Required balanced binary tree is:
29
/ \
21 7
/ \
13 15
Enfoque:
siga los pasos a continuación para resolver el problema:
- Encuentre todos los Nodes hoja en el árbol binario dado y cree una lista doblemente enlazada usándolos.
- Para crear un árbol binario equilibrado a partir de la lista doblemente enlazada anterior, haga lo siguiente:
- Encuentre el Node medio de la lista doblemente enlazada formada arriba y configúrelo como un Node raíz del árbol resultante .
- Itere recursivamente a la izquierda y a la derecha del Node medio actual en la lista doblemente enlazada y repita los pasos anteriores hasta que se cubran todos los Nodes.
- Imprima el árbol binario equilibrado recién creado.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Structure for Linked list and tree
class Node {
public:
int data;
Node *left, *right;
};
// Function that returns the count of
// nodes in the given linked list
int countNodes(Node* head)
{
// Initialize count
int count = 0;
Node* temp = head;
// Iterate till the end of LL
while (temp) {
temp = temp->right;
// Increment the count
count++;
}
// Return the final count
return count;
}
// Function to return the root of
// the newly created balanced binary
// tree from the given doubly LL
Node* sortedListToBSTRecur(
Node** head_ref, int n)
{
// Base Case
if (n <= 0)
return NULL;
// Recursively construct
// the left subtree
Node* left = sortedListToBSTRecur(
head_ref, n / 2);
// head_ref now refers to
// middle node, make middle node
// as root of BST
Node* root = *head_ref;
// Set pointer to left subtree
root->left = left;
// Change head pointer of
// Linked List for parent
// recursive calls
*head_ref = (*head_ref)->right;
// Recursively construct the
// right subtree and link it
// with root
root->right
= sortedListToBSTRecur(
head_ref, n - n / 2 - 1);
// Return the root of Balanced BT
return root;
}
Node* sortedListToBST(Node* head)
{
/*Count the number of
nodes in Linked List */
int n = countNodes(head);
/* Construct BST */
return sortedListToBSTRecur(
&head, n);
}
// Function to find the leaf nodes and
// make the doubly linked list of
// those nodes
Node* extractLeafList(Node* root,
Node** head_ref)
{
// Base cases
if (root == NULL)
return NULL;
if (root->left == NULL
&& root->right == NULL) {
// This node is added to doubly
// linked list of leaves, and
// set right pointer of this
// node as previous head of DLL
root->right = *head_ref;
// Change left pointer
// of previous head
if (*head_ref != NULL)
(*head_ref)->left = root;
// Change head of linked list
*head_ref = root;
// Return new root
return NULL;
}
// Recur for right & left subtrees
root->right = extractLeafList(root->right,
head_ref);
root->left = extractLeafList(root->left,
head_ref);
// Return the root
return root;
}
// Function to allocating new Node
// int Binary Tree
Node* newNode(int data)
{
Node* node = new Node();
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}
// Function for inorder traversal
void print(Node* root)
{
// If root is not NULL
if (root != NULL) {
print(root->left);
// Print the root's data
cout << root->data
<< " ";
print(root->right);
}
}
// Function to display nodes of DLL
void printList(Node* head)
{
while (head) {
// Print the data
cout << head->data << " ";
head = head->right;
}
}
// Driver Code
int main()
{
// Given Binary Tree
Node* head = NULL;
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->right = newNode(6);
root->left->left->left = newNode(7);
root->left->left->right = newNode(8);
root->right->right->left = newNode(9);
root->right->right->right = newNode(10);
// Function Call to extract leaf Node
root = extractLeafList(
root, &head);
// Function Call to create Balanced BT
root = sortedListToBST(head);
// Print Inorder traversal New Balanced BT
print(root);
return 0;
}
Java
// Java program for
// the above approach
import java.util.*;
class GFG{
// Structure for Linked
// list and tree
static class Node
{
public int data;
Node left, right;
};
static Node head;
// Function that returns the
// count of nodes in the given
// linked list
static int countNodes(Node head)
{
// Initialize count
int count = 0;
Node temp = head;
// Iterate till the
// end of LL
while (temp != null)
{
temp = temp.right;
// Increment the count
count++;
}
// Return the final count
return count;
}
// Function to return the root of
// the newly created balanced binary
// tree from the given doubly LL
static Node sortedListToBSTRecur(int n)
{
// Base Case
if (n <= 0)
return null;
// Recursively construct
// the left subtree
Node left = sortedListToBSTRecur(n / 2);
// head now refers to
// middle node, make
// middle node as root of BST
Node root = head;
// Set pointer to left subtree
root.left = left;
// Change head pointer of
// Linked List for parent
// recursive calls
head = head.right;
// Recursively construct the
// right subtree and link it
// with root
root.right = sortedListToBSTRecur(n - n /
2 - 1);
// Return the root
// of Balanced BT
return root;
}
static Node sortedListToBST()
{
// Count the number of
// nodes in Linked List
int n = countNodes(head);
// Construct BST
return sortedListToBSTRecur(n);
}
// Function to find the leaf nodes and
// make the doubly linked list of
// those nodes
static Node extractLeafList(Node root)
{
// Base cases
if (root == null)
return null;
if (root.left == null &&
root.right == null)
{
// This node is added to doubly
// linked list of leaves, and
// set right pointer of this
// node as previous head of DLL
root.right = head;
// Change left pointer
// of previous head
if (head != null)
head.left = root;
// Change head of linked list
head = root;
// Return new root
return head;
}
// Recur for right &
// left subtrees
root.right =
extractLeafList(root.right);
root.left =
extractLeafList(root.left);
// Return the root
return root;
}
// Function to allocating new
// Node int Binary Tree
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = null;
node.right = null;
return node;
}
// Function for inorder traversal
static void print(Node root)
{
// If root is not null
if (root != null)
{
print(root.left);
// Print the root's data
System.out.print(root.data + " ");
print(root.right);
}
}
// Function to display nodes of DLL
static void printList(Node head)
{
while (head != null)
{
// Print the data
System.out.print(head.data + " ");
head = head.right;
}
}
// Driver Code
public static void main(String[] args)
{
// Given Binary Tree
head = null;
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.right = newNode(6);
root.left.left.left = newNode(7);
root.left.left.right = newNode(8);
root.right.right.left = newNode(9);
root.right.right.right = newNode(10);
// Function Call to
// extract leaf Node
root = extractLeafList(root);
// Function Call to create
// Balanced BT
root = sortedListToBST();
// Print Inorder traversal
// New Balanced BT
print(root);
}
}
// This code is contributed by Amit Katiyar
Python3
# Python3 program for the above approach # Structure for Linked list and tree class newNode: def __init__(self, data): self.data = data self.left = None self.right = None head = None # Function that returns the count of # nodes in the given linked list def countNodes(head1): # Initialize count count = 0 temp = head1 # Iterate till the end of LL while (temp): temp = temp.right # Increment the count count += 1 # Return the final count return count # Function to return the root of # the newly created balanced binary # tree from the given doubly LL def sortedListToBSTRecur(n): global head # Base Case if (n <= 0): return None # Recursively construct # the left subtree left = sortedListToBSTRecur(n // 2) # head_ref now refers to # middle node, make middle node # as root of BST root = head # Set pointer to left subtree root.left = left # Change head pointer of # Linked List for parent # recursive calls head = head.right # Recursively construct the # right subtree and link it # with root root.right = sortedListToBSTRecur(n - n // 2 - 1) # Return the root of Balanced BT return root def sortedListToBST(): global head # Count the number of nodes # in Linked List n = countNodes(head) # Construct BST return sortedListToBSTRecur(n) # Function to find the leaf nodes and # make the doubly linked list of # those nodes def extractLeafList(root): global head # Base cases if (root == None): return None if (root.left == None and root.right == None): # This node is added to doubly # linked list of leaves, and # set right pointer of this # node as previous head of DLL root.right = head # Change left pointer # of previous head if (head != None): head.left = root # Change head of linked list head = root # Return new root return head # Recur for right & left subtrees root.right = extractLeafList(root.right) root.left = extractLeafList(root.left) # Return the root return root # Function for inorder traversal def print1(root): # If root is not NULL if (root != None): print1(root.left) # Print the root's data print(root.data, end = " ") print1(root.right) # Function to display nodes of DLL def printList(head): while(head): # Print the data print(head.data, end = " ") head = head.right # Driver Code if __name__ == '__main__': # Given Binary Tree root = newNode(1) root.left = newNode(2) root.right = newNode(3) root.left.left = newNode(4) root.left.right = newNode(5) root.right.right = newNode(6) root.left.left.left = newNode(7) root.left.left.right = newNode(8) root.right.right.left = newNode(9) root.right.right.right = newNode(10) # Function Call to extract leaf Node root = extractLeafList(root) # Function Call to create Balanced BT root = sortedListToBST() # Print Inorder traversal New Balanced BT print1(root) # This code is contributed by ipg2016107
C#
// C# program for the above approach
using System;
class GFG{
// Structure for Linked
// list and tree
public class Node
{
public int data;
public Node left, right;
};
static Node head;
// Function that returns the
// count of nodes in the given
// linked list
static int countNodes(Node head)
{
// Initialize count
int count = 0;
Node temp = head;
// Iterate till the
// end of LL
while (temp != null)
{
temp = temp.right;
// Increment the count
count++;
}
// Return the readonly count
return count;
}
// Function to return the root of
// the newly created balanced binary
// tree from the given doubly LL
static Node sortedListToBSTRecur(int n)
{
// Base Case
if (n <= 0)
return null;
// Recursively construct
// the left subtree
Node left = sortedListToBSTRecur(n / 2);
// head now refers to
// middle node, make
// middle node as root of BST
Node root = head;
// Set pointer to left subtree
root.left = left;
// Change head pointer of
// Linked List for parent
// recursive calls
head = head.right;
// Recursively construct the
// right subtree and link it
// with root
root.right = sortedListToBSTRecur(n - n /
2 - 1);
// Return the root
// of Balanced BT
return root;
}
static Node sortedListToBST()
{
// Count the number of
// nodes in Linked List
int n = countNodes(head);
// Construct BST
return sortedListToBSTRecur(n);
}
// Function to find the leaf nodes and
// make the doubly linked list of
// those nodes
static Node extractLeafList(Node root)
{
// Base cases
if (root == null)
return null;
if (root.left == null &&
root.right == null)
{
// This node is added to doubly
// linked list of leaves, and
// set right pointer of this
// node as previous head of DLL
root.right = head;
// Change left pointer
// of previous head
if (head != null)
head.left = root;
// Change head of linked list
head = root;
// Return new root
return head;
}
// Recur for right &
// left subtrees
root.right = extractLeafList(
root.right);
root.left = extractLeafList(
root.left);
// Return the root
return root;
}
// Function to allocating new
// Node int Binary Tree
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = null;
node.right = null;
return node;
}
// Function for inorder traversal
static void print(Node root)
{
// If root is not null
if (root != null)
{
print(root.left);
// Print the root's data
Console.Write(root.data + " ");
print(root.right);
}
}
// Function to display nodes of DLL
static void printList(Node head)
{
while (head != null)
{
// Print the data
Console.Write(head.data + " ");
head = head.right;
}
}
// Driver Code
public static void Main(String[] args)
{
// Given Binary Tree
head = null;
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.right = newNode(6);
root.left.left.left = newNode(7);
root.left.left.right = newNode(8);
root.right.right.left = newNode(9);
root.right.right.right = newNode(10);
// Function call to
// extract leaf Node
root = extractLeafList(root);
// Function call to create
// Balanced BT
root = sortedListToBST();
// Print Inorder traversal
// New Balanced BT
print(root);
}
}
// This code is contributed by Amit Katiyar
Javascript
<script>
// Javascript program for the above approach
// Structure for Linked
// list and tree
class Node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
let head;
// Function that returns the
// count of nodes in the given
// linked list
function countNodes(head)
{
// Initialize count
let count = 0;
let temp = head;
// Iterate till the
// end of LL
while (temp != null)
{
temp = temp.right;
// Increment the count
count++;
}
// Return the final count
return count;
}
// Function to return the root of
// the newly created balanced binary
// tree from the given doubly LL
function sortedListToBSTRecur(n)
{
// Base Case
if (n <= 0)
return null;
// Recursively construct
// the left subtree
let left = sortedListToBSTRecur(parseInt(n / 2, 10));
// head now refers to
// middle node, make
// middle node as root of BST
let root = head;
// Set pointer to left subtree
root.left = left;
// Change head pointer of
// Linked List for parent
// recursive calls
head = head.right;
// Recursively construct the
// right subtree and link it
// with root
root.right = sortedListToBSTRecur(n - parseInt(n / 2, 10) - 1);
// Return the root
// of Balanced BT
return root;
}
function sortedListToBST()
{
// Count the number of
// nodes in Linked List
let n = countNodes(head);
// Construct BST
return sortedListToBSTRecur(n);
}
// Function to find the leaf nodes and
// make the doubly linked list of
// those nodes
function extractLeafList(root)
{
// Base cases
if (root == null)
return null;
if (root.left == null &&
root.right == null)
{
// This node is added to doubly
// linked list of leaves, and
// set right pointer of this
// node as previous head of DLL
root.right = head;
// Change left pointer
// of previous head
if (head != null)
head.left = root;
// Change head of linked list
head = root;
// Return new root
return head;
}
// Recur for right &
// left subtrees
root.right =
extractLeafList(root.right);
root.left =
extractLeafList(root.left);
// Return the root
return root;
}
// Function to allocating new
// Node int Binary Tree
function newNode(data)
{
let node = new Node(data);
return node;
}
// Function for inorder traversal
function print(root)
{
// If root is not null
if (root != null)
{
print(root.left);
// Print the root's data
document.write(root.data + " ");
print(root.right);
}
}
// Function to display nodes of DLL
function printList(head)
{
while (head != null)
{
// Print the data
document.write(head.data + " ");
head = head.right;
}
}
// Given Binary Tree
head = null;
let root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.right = newNode(6);
root.left.left.left = newNode(7);
root.left.left.right = newNode(8);
root.right.right.left = newNode(9);
root.right.right.right = newNode(10);
// Function Call to
// extract leaf Node
root = extractLeafList(root);
// Function Call to create
// Balanced BT
root = sortedListToBST();
// Print Inorder traversal
// New Balanced BT
print(root);
// This code is contributed by mukesh07.
</script>
Producción:
7 8 5 9 10
Complejidad de tiempo: O(N) , donde N es el número de Nodes en el árbol dado.
Complejidad del espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por MohammadMudassir y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA