Los mapas son contenedores asociativos que almacenan elementos. Los mapas se implementan mediante árboles de búsqueda autoequilibrados. En C++ STL usa Red-Black Tree .
Aquí vamos a implementar una clase Map personalizada que tiene un valor entero como clave y el valor almacenado correspondiente a cualquier clave también es de tipo entero.
Lo implementaremos usando el árbol AVL . Para implementar el mapa, primero crearemos un archivo de encabezado que incorporará las funcionalidades de una clase de mapa. A continuación se muestra la estructura básica de la clase Map :
Estructura de la clase Mapa:
La estructura del árbol AVL depende de la estructura del Node:
- Cada Node tiene punteros para el hijo izquierdo , el hijo derecho y el padre .
- Cada Node tiene tres valores primero (que es la clave), segundo (que es el valor de la clave correspondiente) y profundidad (altura del subárbol para el Node).
- La clase de mapa también tiene un valor estático cnt que almacena la cantidad de elementos presentes en el mapa y un Node raíz estático , que es la raíz del árbol.
Almacene esto en un archivo de encabezado (digamos map.h )
C++
class Map {
static class Map* root;
// Number of elements in the map
static int cnt;
// Left child, right child and parent
Map *left, *right, *par;
// First is key, second is value
// and depth is height of the subtree
// for the given node
int first, second, depth;
};
Funciones/Operaciones que se implementarán usando un mapa personalizado
Cubriremos las siguientes funcionalidades y métodos en nuestro mapa:
- insertar()
- encontrar()
- actualizar()
- acceder a cualquier tecla
- clear()
- contar()
- Talla()
- vacío()
- clear()
- iterar el mapa
Los métodos y funcionalidades se discuten a continuación:
1. insertar():
Este método se utiliza para insertar un par clave-valor en el mapa. Aquí se utilizan dos métodos insert().
Uno se hace público y toma dos parámetros:
- primero – es la clave
- segundo – Es el valor respectivo de la clave
Sintaxis:
map.insert(primero, segundo);
A continuación se muestra la implementación de este método.
C++
void insert(int first, int second)
{
Map* temp = iterator(first);
// If element doesnot exist already
if (temp == nullptr)
insert(first)->second = second;
// If element exists already update it
else
temp->second = second;
}
Complejidad de tiempo: O(logN) donde N es el tamaño del mapa
El otro se hace privado. Este método se llama dentro de la función de sobrecarga del operador de [] .
- Toma solo un parámetro: primero (Es la clave).
- Crea el nuevo Node con » primero » como clave y devuelve la instancia del Node.
Sintaxis:
mapa[primero] = segundo;
A continuación se muestra la implementación de este método:
C++
Map* insert(int first)
{
// Increase the number of elements
cnt++;
Map* newnode = create(first);
// If empty tree simply create the root
if (root == nullptr) {
root = newnode;
return root;
}
Map *temp = root, *prev = nullptr;
while (temp != nullptr) {
prev = temp;
if (first < temp->first)
temp = temp->left;
else if (first > temp->first)
temp = temp->right;
else {
free(newnode);
// If element already exists
// decrease the count
cnt--;
// If the key is found then it is
// returned by reference so that it is
// updatable
return temp;
}
}
if (first < prev->first)
prev->left = newnode;
else
prev->right = newnode;
newnode->par = prev;
// Once inserted Check and balance the tree
// at every node in path from "newnode" to "root"
balance(newnode);
// New object is inserted and returned to
// initialize in the main during assignment
return newnode;
}
int& operator[](int key) {
return insert(key)->second;
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa
2. buscar():
Se utiliza para encontrar un elemento. Este es un método público. Toma un parámetro: primero (que es la clave) y devuelve la referencia asociada a la clave. Internamente llama al método privado iterator() para encontrar la clave
Sintaxis:
map.find(primero);
A continuación se muestra la implementación del método.
C++
Map* iterator(int first)
{
Map* temp = root;
while (temp != nullptr && temp->first != first) {
if (first < temp->first) {
temp = temp->left;
}
else {
temp = temp->right;
}
}
return temp;
}
Map* find(int first) {
return iterator(first);
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa.
3. actualizar():
Este valor se utiliza para actualizar el valor asociado a una clave. Este es un método público. Toma dos parámetros:
- primero: Es la clave que hay que encontrar.
- segundo: Es el nuevo valor de la clave.
La función llama a la función iterator() para obtener la instancia de la clave y actualiza el valor asociado a esa clave. Si no existe tal clave, entonces no se realiza ninguna operación.
Sintaxis:
map.update(primero, segundo);
A continuación se muestra la implementación del método.
C++
void update(int first, int second)
{
Map* temp = iterator(first);
if (temp != nullptr) {
temp->second = second;
}
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa
4. Acceder a cualquier tecla:
Se puede acceder a cualquier valor usando el operador de subíndice [] . El concepto de sobrecarga de métodos se utiliza para implementar la funcionalidad. Es un método público y la función de búsqueda() se llama dentro de la función de sobrecarga. Toma un parámetro: primero (es el valor de la clave)
Sintaxis:
mapa[primero];
A continuación se muestra la implementación del método.
C++
const Map* iterator(int first) const
{
Map* temp = root;
while (temp != nullptr
&& temp->first != first) {
if (first < temp->first)
temp = temp->left;
else
temp = temp->right;
}
return temp;
}
const int search(int first) const
{
const Map* temp = iterator(first);
// If element exists with the given key
// return its value
if (temp != nullptr)
return temp->second;
// If element doesn't exist
// return default value of 0
return 0;
}
const int operator[](int key) const
{
// Search method is also qualified with const
return search(key);
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa.
5. clear():
Elimina el Node con la clave dada y lo reemplaza con su predecesor en orden o su sucesor en orden. Es un método público. Toma un parámetro: primero (es la clave cuyo valor debe eliminarse). Al final de la función, llama al método balance() en el padre de ese Node que reemplazó al Node eliminado para equilibrar el árbol AVL.
Sintaxis:
map.erase(primero);
A continuación se muestra la implementación del método.
C++
void erase(int first, Map* temp = root)
{
Map* prev = 0;
cnt--;
while (temp != 0 && temp->first != first) {
prev = temp;
if (first < temp->first) {
temp = temp->left;
}
else if (first > temp->first) {
temp = temp->right;
}
}
if (temp == nullptr) {
cnt++;
return;
}
if (cnt == 0 && temp == root) {
free(temp);
root = nullptr;
return;
}
Map* l = inorderPredecessor(temp->left);
Map* r = inorderSuccessor(temp->right);
if (l == 0 && r == 0) {
if (prev == 0) {
root = 0;
}
else {
if (prev->left == temp) {
prev->left = 0;
}
else {
prev->right = 0;
}
free(temp);
balance(prev);
}
return;
}
Map* start;
if (l != 0) {
if (l == temp->left) {
l->right = temp->right;
if (l->right != 0) {
l->right->par = l;
}
start = l;
}
else {
if (l->left != 0) {
l->left->par = l->par;
}
start = l->par;
l->par->right = l->left;
l->right = temp->right;
l->par = 0;
if (l->right != 0) {
l->right->par = l;
}
l->left = temp->left;
temp->left->par = l;
}
if (prev == 0) {
root = l;
}
else {
if (prev->left == temp) {
prev->left = l;
l->par = prev;
}
else {
prev->right = l;
l->par = prev;
}
free(temp);
}
balance(start);
return;
}
else {
if (r == temp->right) {
r->left = temp->left;
if (r->left != 0) {
r->left->par = r;
}
start = r;
}
else {
if (r->right != 0) {
r->right->par = r->par;
}
start = r->par;
r->par->left = r->right;
r->left = temp->left;
r->par = 0;
if (r->left != 0) {
r->left->par = r;
}
r->right = temp->right;
temp->right->par = r;
}
if (prev == 0) {
root = r;
}
else {
if (prev->right == temp) {
prev->right = r;
r->par = prev;
}
else {
prev->left = r;
r->par = prev;
}
free(temp);
}
balance(start);
return;
}
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa.
6. cuenta():
Este método devuelve el recuento de una clave en el mapa. Este es un método público. Toma un parámetro: primero (que es la clave de valor cuyo conteo se debe encontrar). Este método llama internamente al método iterator() y, si no se encuentra ningún Node, el recuento es 0 . De lo contrario, count devuelve 1 .
Sintaxis:
map.count(primero);
A continuación se muestra la implementación del método.
C++
int count(int first)
{
Map* temp = iterator(first);
// If key is found
if (temp != nullptr)
return 1;
// If key is not found
return 0;
}
Complejidad temporal: O(logN) donde N es el tamaño del mapa.
7. tamaño():
Este método devuelve el tamaño del mapa. Este es un método público. Este método no toma ningún parámetro.
Sintaxis:
Tamaño de mapa();
A continuación se muestra la implementación del método.
C++
int size(void) {
return cnt;
}
Complejidad de tiempo: O(1)
8. vacío():
Este método comprueba si el mapa está vacío o no. Este es un método público. Devuelve verdadero si el mapa está vacío, de lo contrario, falso. Este método no toma ningún parámetro.
Sintaxis:
mapa.vacío();
A continuación se muestra la implementación del método.
C++
bool empty(void)
{
if (root == 0)
return true;
return false;
}
Complejidad de tiempo: O(1)
9. clear():
Este método se utiliza para eliminar todo el mapa. Este es un método público. No toma ningún parámetro. Toma el método erase() internamente.
Sintaxis:
mapa.clear();
A continuación se muestra la implementación del método.
C++
void clear(void)
{
while (root != nullptr) {
erase(root->first);
}
}
Complejidad de tiempo: O(N * logN) donde N es el tamaño del mapa
10. iterar():
Este método se utiliza para recorrer todo el mapa. Este es un método público. Tampoco toma ningún parámetro. Los Nodes se imprimen en forma ordenada de clave.
Sintaxis:
mapa.iterar();
A continuación se muestra la implementación del método.
C++
void iterate(Map* head = root)
{
if (root == 0)
return;
if (head->left != 0) {
iterate(head->left);
}
cout << head->first << ' ';
if (head->right != 0) {
iterate(head->right);
}
}
Complejidad temporal: O(N) donde N es el tamaño del mapa
Creación de encabezado de mapa personalizado
C++
// map.h
// C++ Program to implement Map class(using AVL tree)
// This is a header file map.h and doesnot contain main()
#include <iostream>
using namespace std;
// Custom Map Class
class Map {
private:
Map* iterator(int first)
{
// A temporary variable created
// so that we do not
// loose the "root" of the tree
Map* temp = root;
// Stop only when either the key is found
// or we have gone further the leaf node
while (temp != nullptr &&
temp->first != first) {
// Go to left if key is less than
// the key of the traversed node
if (first < temp->first) {
temp = temp->left;
}
// Go to right otherwise
else {
temp = temp->right;
}
}
// If there doesn't exist any element
// with first as key, nullptr is returned
return temp;
}
// Returns the pointer to element
// whose key matches first.
// Specially created for search method
// (because search() is const qualified).
const Map* iterator(int first) const
{
Map* temp = root;
while (temp != nullptr
&& temp->first != first) {
if (first < temp->first) {
temp = temp->left;
}
else {
temp = temp->right;
}
}
return temp;
}
// The const property is used to keep the
// method compatible with the method "const
// int&[]operator(int) const"
// Since we are not allowed to change
// the class attributes in the method
// "const int&[]operator(int) const"
// we have to assure the compiler that
// method called(i.e "search") inside it
// doesn't change the attributes of class
const int search(int first) const
{
const Map* temp = iterator(first);
if (temp != nullptr) {
return temp->second;
}
return 0;
}
// Utiliity function to return the Map* object
// with its members initialized
// to default values except the key
Map* create(int first)
{
Map* newnode = (Map*)malloc(sizeof(Map));
newnode->first = first;
newnode->second = 0;
newnode->left = nullptr;
newnode->right = nullptr;
newnode->par = nullptr;
// Depth of a newnode shall be 1
// and not zero to differentiate
// between no child (which returns
// nullptr) and having child(returns 1)
newnode->depth = 1;
return newnode;
}
// All the rotation operation are performed
// about the node itself
// Performs all the linking done when there is
// clockwise rotation performed at node "x"
void right_rotation(Map* x)
{
Map* y = x->left;
x->left = y->right;
if (y->right != nullptr) {
y->right->par = x;
}
if (x->par != nullptr && x->par->right == x) {
x->par->right = y;
}
else if (x->par != nullptr && x->par->left == x) {
x->par->left = y;
}
y->par = x->par;
y->right = x;
x->par = y;
}
// Performs all the linking done when there is
// anti-clockwise rotation performed at node "x"
void left_rotation(Map* x)
{
Map* y = x->right;
x->right = y->left;
if (y->left != nullptr) {
y->left->par = x;
}
if (x->par != nullptr && x->par->left == x) {
x->par->left = y;
}
else if (x->par != nullptr && x->par->right == x) {
x->par->right = y;
}
y->par = x->par;
y->left = x;
x->par = y;
}
// Draw the initial and final graph of each
// case(take case where every node has two child)
// and update the nodes depth before any rotation
void helper(Map* node)
{
// If left skewed
if (depthf(node->left)
- depthf(node->right) > 1) {
// If "depth" of left subtree of
// left child of "node" is
// greater than right
// subtree of left child of "node"
if (depthf(node->left->left)
> depthf(node->left->right)) {
node->depth
= max(depthf(node->right) + 1,
depthf(node->left->right) + 1);
node->left->depth
= max(depthf(node->left->left) + 1,
depthf(node) + 1);
right_rotation(node);
}
// If "depth" of right subtree
// of left child of "node" is
// greater than
// left subtree of left child
else {
node->left->depth = max(
depthf(node->left->left) + 1,
depthf(node->left->right->left)
+ 1);
node->depth
= max(depthf(node->right) + 1,
depthf(node->left->right->right) + 1);
node->left->right->depth
= max(depthf(node) + 1,
depthf(node->left) + 1);
left_rotation(node->left);
right_rotation(node);
}
}
// If right skewed
else if (depthf(node->left)
- depthf(node->right) < -1) {
// If "depth" of right subtree of right
// child of "node" is greater than
// left subtree of right child
if (depthf(node->right->right)
> depthf(node->right->left)) {
node->depth
= max(depthf(node->left) + 1,
depthf(node->right->left) + 1);
node->right->depth
= max(depthf(node->right->right) + 1,
depthf(node) + 1);
left_rotation(node);
}
// If "depth" of left subtree
// of right child of "node" is
// greater than that of right
// subtree of right child of "node"
else {
node->right->depth = max(
depthf(node->right->right) + 1,
depthf(node->right->left->right) + 1);
node->depth = max(
depthf(node->left) + 1,
depthf(node->right->left->left) + 1);
node->right->left->depth
= max(depthf(node) + 1,
depthf(node->right) + 1);
right_rotation(node->right);
left_rotation(node);
}
}
}
// Balancing the tree about the "node"
void balance(Map* node)
{
while (node != root) {
int d = node->depth;
node = node->par;
if (node->depth < d + 1) {
node->depth = d + 1;
}
if (node == root
&& depthf(node->left)
- depthf(node->right) > 1) {
if (depthf(node->left->left)
> depthf(node->left->right)) {
root = node->left;
}
else {
root = node->left->right;
}
helper(node);
break;
}
else if (node == root
&& depthf(node->left)
- depthf(node->right)
< -1) {
if (depthf(node->right->right)
> depthf(node->right->left)) {
root = node->right;
}
else {
root = node->right->left;
}
helper(node);
break;
}
helper(node);
}
}
// Utility method to return the
// "depth" of the subtree at the "node"
int depthf(Map* node)
{
if (node == nullptr)
// If it is null node
return 0;
return node->depth;
}
// Function to insert a value in map
Map* insert(int first)
{
cnt++;
Map* newnode = create(first);
if (root == nullptr) {
root = newnode;
return root;
}
Map *temp = root, *prev = nullptr;
while (temp != nullptr) {
prev = temp;
if (first < temp->first) {
temp = temp->left;
}
else if (first > temp->first) {
temp = temp->right;
}
else {
free(newnode);
cnt--;
return temp;
}
}
if (first < prev->first) {
prev->left = newnode;
}
else {
prev->right = newnode;
}
newnode->par = prev;
balance(newnode);
return newnode;
}
// Returns the previous node in
// inorder traversal of the AVL Tree.
Map* inorderPredecessor(Map* head)
{
if (head == nullptr)
return head;
while (head->right != nullptr) {
head = head->right;
}
return head;
}
// Returns the next node in
// inorder traversal of the AVL Tree.
Map* inorderSuccessor(Map* head)
{
if (head == nullptr)
return head;
while (head->left != nullptr) {
head = head->left;
}
return head;
}
public:
// Root" is kept static because it's a class
// property and not an instance property
static class Map* root;
static int cnt;
// "first" is key and "second" is value
Map *left, *right, *par;
int first, second, depth;
// overloaded [] operator for assignment or
// inserting a key-value pairs in the map
// since it might change the members of
// the class therefore this is
// invoked when any assignment is done
int& operator[](int key) {
return insert(key)->second;
}
// Since we have two methods with
// the same name "[]operator(int)" and
// methods/functions cannot be
// distinguished by their return types
// it is mandatory to include a const
// qualifier at the end of any of the methods
// This method will be called from a const
// reference to the object of Map class
// It will not be called for assignment
// because it doesn't allow to change
// member variables
// We cannot make it return by reference
// because the variable "temp" returned
// by the "search" method is
// statically allocated and therefore
// it's been destroyed when it is called out
const int operator[](int key) const
{
return search(key);
}
// Count returns whether an element
// exists in the Map or not
int count(int first)
{
Map* temp = iterator(first);
if (temp != nullptr) {
return 1;
}
return 0;
}
// Returns number of elements in the map
int size(void) {
return cnt;
}
// Removes an element given its key
void erase(int first, Map* temp = root)
{
Map* prev = nullptr;
cnt--;
while (temp != nullptr &&
temp->first != first) {
prev = temp;
if (first < temp->first) {
temp = temp->left;
}
else if (first > temp->first) {
temp = temp->right;
}
}
if (temp == nullptr) {
cnt++;
return;
}
if (cnt == 0 && temp == root) {
free(temp);
root = nullptr;
return;
}
Map* l
= inorderPredecessor(temp->left);
Map* r
= inorderSuccessor(temp->right);
if (l == nullptr && r == nullptr) {
if (prev == nullptr) {
root = nullptr;
}
else {
if (prev->left == temp) {
prev->left = nullptr;
}
else {
prev->right = nullptr;
}
free(temp);
balance(prev);
}
return;
}
Map* start;
if (l != nullptr) {
if (l == temp->left) {
l->right = temp->right;
if (l->right != nullptr) {
l->right->par = l;
}
start = l;
}
else {
if (l->left != nullptr) {
l->left->par = l->par;
}
start = l->par;
l->par->right = l->left;
l->right = temp->right;
l->par = nullptr;
if (l->right != nullptr) {
l->right->par = l;
}
l->left = temp->left;
temp->left->par = l;
}
if (prev == nullptr) {
root = l;
}
else {
if (prev->left == temp) {
prev->left = l;
l->par = prev;
}
else {
prev->right = l;
l->par = prev;
}
free(temp);
}
balance(start);
return;
}
else {
if (r == temp->right) {
r->left = temp->left;
if (r->left != nullptr) {
r->left->par = r;
}
start = r;
}
else {
if (r->right != nullptr) {
r->right->par = r->par;
}
start = r->par;
r->par->left = r->right;
r->left = temp->left;
r->par = nullptr;
if (r->left != nullptr) {
r->left->par = r;
}
r->right = temp->right;
temp->right->par = r;
}
if (prev == nullptr) {
root = r;
}
else {
if (prev->right == temp) {
prev->right = r;
r->par = prev;
}
else {
prev->left = r;
r->par = prev;
}
free(temp);
}
balance(start);
return;
}
}
// Returns if the map is empty or not
bool empty(void)
{
if (root == nullptr)
return true;
return false;
}
// Given the key of an element it updates
// the value of the key
void update(int first, int second)
{
Map* temp = iterator(first);
if (temp != nullptr) {
temp->second = second;
}
}
// Deleting the root of
// the tree each time until the map
// is not empty
void clear(void)
{
while (root != nullptr) {
erase(root->first);
}
}
// Inorder traversal of the AVL tree
void iterate(Map* head = root)
{
if (root == nullptr)
return;
if (head->left != nullptr) {
iterate(head->left);
}
cout << head->first << ' ';
if (head->right != nullptr) {
iterate(head->right);
}
}
// Returns a pointer/iterator to the element
// whose key is first
Map* find(int first) {
return iterator(first);
}
// Overloaded insert method,
// takes two parameters - key and value
void insert(int first, int second)
{
Map* temp = iterator(first);
if (temp == nullptr) {
insert(first)->second = second;
}
else {
temp->second = second;
}
}
};
Map* Map::root = nullptr;
int Map::cnt = 0;
Ahora guárdelo como un archivo de encabezado, diga map.h para incluirlo en otros códigos e implementar las funcionalidades.
Cómo ejecutar el mapa personalizado construido
A continuación se menciona el procedimiento a seguir para la implementación del mapa:
- Primero cree un archivo de encabezado para el mapa ( map.h )
- Luego almacene el encabezado en la misma carpeta en la que se almacenan los archivos que implementan el mapa.
- Incluya el encabezado del mapa en los archivos que implementarán la clase de mapa.
- Compile y ejecute los archivos que implementan el mapa.
Ejemplos para mostrar el uso de Mapa personalizado
Los siguientes programas demuestran la ejecución de la clase Map creando sus funcionalidades.
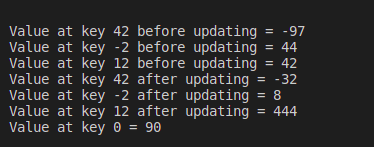
Ejemplo 1: Programas para demostrar el uso de insert(), accediendo a cualquier tecla y métodos update():
C++
#include "map.h"
#include <iostream>
using namespace std;
int main()
{
Map map;
// 1st way of insertion
map[132] = 3;
map[34] = 5;
map[42] = -97;
map[22] = 10;
map[12] = 42;
// 2nd way of insertion
map.insert(-2,44);
map.insert(0,90);
// accessing elements
cout<<"Value at key 42 before updating = "
<<map[42]<<endl;
cout<<"Value at key -2 before updating = "
<<map[-2]<<endl;
cout<<"Value at key 12 before updating = "
<<map[12]<<endl;
// Updating value at key 42
map[42] = -32;
// Updating value at key -2
map.insert(-2,8);
// Updating value at key 12
map.update(12,444);
// accessing elements
cout<<"Value at key 42 after updating = "
<<map[42]<<endl;
cout<<"Value at key -2 after updating = "
<<map[-2]<<endl;
cout<<"Value at key 12 after updating = "
<<map[12]<<endl;
cout<<"Value at key 0 = "<<map[0]<<endl;
return 0;
}
Producción:
Ejemplo 2: Programa para demostrar el uso de los métodos erase(), clear() e iterate():
C++
#include "map.h"
#include <iostream>
using namespace std;
int main()
{
Map map;
map[132] = 3;
map[34] = 5;
map[42] = -97;
map[22] = 10;
map[12] = 42;
// Iterating the Map elements before erasing 22
map.iterate();
map.erase(22);
// Iterating the Map elements after erasing 22
map.iterate();
// Deleting the whole map
map.clear();
// Now since there are zero elements
// in the Map the output is blank
cout<<"\nElements in Map after clear operation: ";
map.iterate();
return 0;
}
Producción:

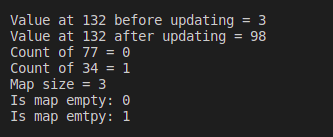
Ejemplo 3: Programa para demostrar el uso de los métodos find(), count(), empty() y size():
C++
#include "map.h"
#include <iostream>
using namespace std;
int main()
{
Map map;
map[132] = 3;
map[34] = 5;
map[42] = -97;
cout<<"Value at 132 before updating = "
<<map[132]<<endl;
// Find method returns pointer to element
// whose key matches given key
Map *it = map.find(132);
// Updating the value at key 132
it->second = 98;
cout<<"Value at 132 after updating = "
<<map[132]<<endl;
// Count of an element which is not present
// in the map is 0
cout<<"Count of 77 = "<<map.count(77)<<endl;
// Count of an element which is present
// in the map is 1
cout<<"Count of 34 = "<<map.count(34)<<endl;
// Size of map/number of elements in map
cout<<"Map size = "<<map.size()<<endl;
// Map is not empty therefore returned 0
cout<<"Is map empty: "<<map.empty()<<endl;
// Clearing the map
map.clear();
// Map is empty therefore return 1
cout<<"Is map emtpy: "<<map.empty()<<endl;
return 0;
}
Producción:
Publicación traducida automáticamente
Artículo escrito por abhishekkumartbbt y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA