Requisitos previos : Scipy
La respuesta de impulso de un filtro gaussiano se escribe como una función gaussiana de la siguiente manera:
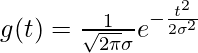
Su resultado también es gaussiano. En este artículo, trazaremos el pulso de Gauss a 3 Hz utilizando la biblioteca de Python scipy y matplotlib . El pulso de Gauss se utiliza en filtros digitales para el análisis de movimiento. Para crear un pulso gauss, se usa el método gausspulse() de scipy. gausspulse() devuelve un pulso sinusoidal modulado por Gauss de amplitud unitaria en los tiempos indicados en la array t, con una frecuencia central ‘fc’ en hercios (Hz).
Sintaxis: scipy.signal.gausspulse(t, fc retquad, retenv)
Parámetro:
- t: Array de entrada.
- fc: Frecuencia central.
- retquad: Si es Verdadero, devuelve tanto la parte real como la imaginaria de la señal. El valor predeterminado es Falso.
- retenv: si es verdadero, devuelve la envolvente de la señal. El valor predeterminado es Falso.
Devoluciones
- yI: La parte real de la señal. Siempre regresado.
- yQ: Parte imaginaria de la señal. Solo se devuelve si retquad es Verdadero.
- yenv: La envolvente de la señal. Solo se devuelve si retenv es True.
Acercarse:
- Importar módulo requerido.
- Cree una array de datos usando np.linespace.
- Cree un pulso de Gauss a 3 Hz.
- Etiqueta el gráfico.
- Muestre el gráfico resultante.
La implementación utilizando el enfoque anterior se describe a continuación:
Python3
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
t = np.linspace(-1, 1, 200)
i, q, e = signal.gausspulse(t, fc=3, retquad=True, retenv=True)
plt.plot(i, color='green')
plt.plot(q, color='black')
plt.plot(e, '--', color='red')
plt.title('Gauss pulse for a 3 Hz - Geeksforgeeks')
plt.ylabel("Normalized magnitude [dB]")
plt.xlabel("Normalized frequency [cycles per sample]")
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.legend(['Inphase', 'Quadrature', 'Envelope'])
plt.show()
Producción:
