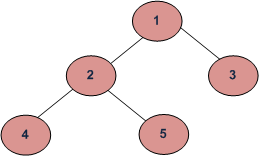
Hemos discutido el recorrido del orden de niveles de un árbol en la publicación anterior. La idea es imprimir primero el último nivel, luego el penúltimo nivel, y así sucesivamente. Al igual que el recorrido de orden de nivel, cada nivel se imprime de izquierda a derecha.
C++
// A recursive C++ program to print
// REVERSE level order traversal
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data,
pointer to left and right child */
class node
{
public:
int data;
node* left;
node* right;
};
/*Function prototypes*/
void printGivenLevel(node* root, int level);
int height(node* node);
node* newNode(int data);
/* Function to print REVERSE
level order traversal a tree*/
void reverseLevelOrder(node* root)
{
int h = height(root);
int i;
for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1)
{
printGivenLevel(root->left, level - 1);
printGivenLevel(root->right, level - 1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(node* node)
{
if (node == NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return(lheight + 1);
else return(rheight + 1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return(Node);
}
/* Driver code*/
int main()
{
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n";
reverseLevelOrder(root);
return 0;
}
// This code is contributed by rathbhupendra
C
// A recursive C program to print REVERSE level order traversal
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left and right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/*Function prototypes*/
void printGivenLevel(struct node* root, int level);
int height(struct node* node);
struct node* newNode(int data);
/* Function to print REVERSE level order traversal a tree*/
void reverseLevelOrder(struct node* root)
{
int h = height(root);
int i;
for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(struct node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return(lheight+1);
else return(rheight+1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Level Order traversal of binary tree is \n");
reverseLevelOrder(root);
return 0;
}
Java
// A recursive java program to print reverse level order traversal
// A binary tree node
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Function to print REVERSE level order traversal a tree*/
void reverseLevelOrder(Node node)
{
int h = height(node);
int i;
for (i = h; i >= 1; i--)
//THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
{
printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
void printGivenLevel(Node node, int level)
{
if (node == null)
return;
if (level == 1)
System.out.print(node.data + " ");
else if (level > 1)
{
printGivenLevel(node.left, level - 1);
printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(Node node)
{
if (node == null)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node.left);
int rheight = height(node.right);
/* use the larger one */
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Level Order traversal of binary tree is : ");
tree.reverseLevelOrder(tree.root);
}
}
// This code has been contributed by Mayank Jaiswal
Python
# A recursive Python program to print REVERSE level order traversal # A binary tree node class Node: # Constructor to create a new node def __init__(self, data): self.data = data self.left = None self.right = None # Function to print reverse level order traversal def reverseLevelOrder(root): h = height(root) for i in reversed(range(1, h+1)): printGivenLevel(root,i) # Print nodes at a given level def printGivenLevel(root, level): if root is None: return if level ==1 : print root.data, elif level>1: printGivenLevel(root.left, level-1) printGivenLevel(root.right, level-1) # Compute the height of a tree-- the number of # nodes along the longest path from the root node # down to the farthest leaf node def height(node): if node is None: return 0 else: # Compute the height of each subtree lheight = height(node.left) rheight = height(node.right) # Use the larger one if lheight > rheight : return lheight + 1 else: return rheight + 1 # Driver program to test above function root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "Level Order traversal of binary tree is" reverseLevelOrder(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// A recursive C# program to print
// reverse level order traversal
using System;
// A binary tree node
class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Function to print REVERSE
level order traversal a tree*/
void reverseLevelOrder(Node node)
{
int h = height(node);
int i;
for (i = h; i >= 1; i--)
// THE ONLY LINE DIFFERENT
// FROM NORMAL LEVEL ORDER
{
printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
void printGivenLevel(Node node, int level)
{
if (node == null)
return;
if (level == 1)
Console.Write(node.data + " ");
else if (level > 1)
{
printGivenLevel(node.left, level - 1);
printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree --
the number of nodes along the longest
path from the root node down to the
farthest leaf node.*/
int height(Node node)
{
if (node == null)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node.left);
int rheight = height(node.right);
/* use the larger one */
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Driver Code
static public void Main(String []args)
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown
// in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Level Order traversal " +
"of binary tree is : ");
tree.reverseLevelOrder(tree.root);
}
}
// This code is contributed
// by Arnab Kundu
Javascript
<script>
// A recursive JavaScript program to print
// reverse level order traversal
// A binary tree node
class Node {
constructor(item) {
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
/* Function to print REVERSE
level order traversal a tree*/
reverseLevelOrder(node) {
var h = this.height(node);
var i;
for (
i = h;
i >= 1;
i-- // THE ONLY LINE DIFFERENT // FROM NORMAL LEVEL ORDER
) {
this.printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
printGivenLevel(node, level) {
if (node == null) return;
if (level == 1) document.write(node.data + " ");
else if (level > 1) {
this.printGivenLevel(node.left, level - 1);
this.printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree --
the number of nodes along the longest
path from the root node down to the
farthest leaf node.*/
height(node) {
if (node == null) return 0;
else {
/* compute the height of each subtree */
var lheight = this.height(node.left);
var rheight = this.height(node.right);
/* use the larger one */
if (lheight > rheight) return lheight + 1;
else return rheight + 1;
}
}
}
// Driver Code
var tree = new BinaryTree();
// Let us create trees shown
// in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
document.write(
"Level Order traversal " + "of binary tree is : <br>"
);
tree.reverseLevelOrder(tree.root);
</script>
C++
// A C++ program to print REVERSE level order traversal using stack and queue
// This approach is adopted from following link
// http://tech-queries.blogspot.in/2008/12/level-order-tree-traversal-in-reverse.html
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left and right children */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* Given a binary tree, print its nodes in reverse level order */
void reverseLevelOrder(node* root)
{
stack <node *> S;
queue <node *> Q;
Q.push(root);
// Do something like normal level order traversal order. Following are the
// differences with normal level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.empty() == false)
{
/* Dequeue node and make it root */
root = Q.front();
Q.pop();
S.push(root);
/* Enqueue right child */
if (root->right)
Q.push(root->right); // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
/* Enqueue left child */
if (root->left)
Q.push(root->left);
}
// Now pop all items from stack one by one and print them
while (S.empty() == false)
{
root = S.top();
cout << root->data << " ";
S.pop();
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
node* temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return (temp);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
cout << "Level Order traversal of binary tree is \n";
reverseLevelOrder(root);
return 0;
}
Java
// A recursive java program to print reverse level order traversal
// using stack and queue
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/* A binary tree node has data, pointer to left and right children */
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Given a binary tree, print its nodes in reverse level order */
void reverseLevelOrder(Node node)
{
Stack<Node> S = new Stack();
Queue<Node> Q = new LinkedList();
Q.add(node);
// Do something like normal level order traversal order.Following
// are the differences with normal level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.isEmpty() == false)
{
/* Dequeue node and make it root */
node = Q.peek();
Q.remove();
S.push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.add(node.right);
/* Enqueue left child */
if (node.left != null)
Q.add(node.left);
}
// Now pop all items from stack one by one and print them
while (S.empty() == false)
{
node = S.peek();
System.out.print(node.data + " ");
S.pop();
}
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
System.out.println("Level Order traversal of binary tree is :");
tree.reverseLevelOrder(tree.root);
}
}
// This code has been contributed by Mayank Jaiswal
Python
# Python program to print REVERSE level order traversal using # stack and queue from collections import deque # A binary tree node class Node: # Constructor to create a new node def __init__(self, data): self.data = data self.left = None self.right = None # Given a binary tree, print its nodes in reverse level order def reverseLevelOrder(root): # we can use a double ended queue which provides O(1) insert at the beginning # using the appendleft method # we do the regular level order traversal but instead of processing the # left child first we process the right child first and the we process the left child # of the current Node # we can do this One pass reduce the space usage not in terms of complexity but intuitively q = deque() q.append(root) ans = deque() while q: node = q.popleft() if node is None: continue ans.appendleft(node.data) if node.right: q.append(node.right) if node.left: q.append(node.left) return ans # Driver program to test above function root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.left = Node(6) root.right.right = Node(7) print "Level Order traversal of binary tree is" reverseLevelOrder(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// A recursive C# program to print reverse
// level order traversal using stack and queue
using System.Collections.Generic;
using System;
/* A binary tree node has data,
pointer to left and right children */
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
public class BinaryTree
{
Node root;
/* Given a binary tree, print its
nodes in reverse level order */
void reverseLevelOrder(Node node)
{
Stack<Node> S = new Stack<Node>();
Queue<Node> Q = new Queue<Node>();
Q.Enqueue(node);
// Do something like normal level
// order traversal order.Following
// are the differences with normal
// level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.Count>0)
{
/* Dequeue node and make it root */
node = Q.Peek();
Q.Dequeue();
S.Push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.Enqueue(node.right);
/* Enqueue left child */
if (node.left != null)
Q.Enqueue(node.left);
}
// Now pop all items from stack
// one by one and print them
while (S.Count>0)
{
node = S.Peek();
Console.Write(node.data + " ");
S.Pop();
}
}
// Driver code
public static void Main()
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Console.WriteLine("Level Order traversal of binary tree is :");
tree.reverseLevelOrder(tree.root);
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// A recursive javascript program to print
// reverse level order traversal
// using stack and queue
/* A binary tree node has data, pointer to left
and right children */
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right=null;
}
}
let root;
/* Given a binary tree, print its nodes in reverse level order */
function reverseLevelOrder(node)
{
let S = [];
let Q = [];
Q.push(node);
// Do something like normal
// level order traversal order.Following
// are the differences with normal
// level order traversal
// 1) Instead of printing a node,
// we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.length != 0)
{
/* Dequeue node and make it root */
node = Q[0];
Q.shift();
S.push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.push(node.right);
/* Enqueue left child */
if (node.left != null)
Q.push(node.left);
}
// Now pop all items from stack
// one by one and print them
while (S.length != 0)
{
node = S.pop();
document.write(node.data + " ");
}
}
// Driver program to test above functions
// Let us create trees shown in above diagram
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
document.write("Level Order traversal of binary tree is :<br>");
reverseLevelOrder(root);
// This code is contributed by avanitrachhadiya2155
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA