Contar caminos pares en Binary Tree

Dado un árbol binario , la tarea es contar el número de caminos pares en el árbol binario dado. Even Path es una ruta en la que la ruta de raíz a hoja contiene todos los Nodes pares solamente.

Ejemplos: 

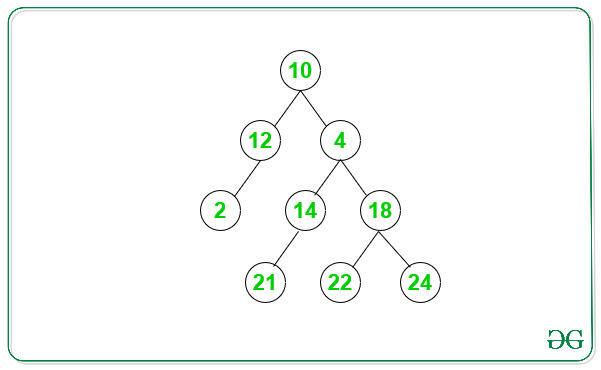
Entrada: A continuación se muestra el árbol binario dado: 
 

Salida: 3 
Explicación: 
Hay 3 rutas pares para el árbol binario anterior: 
1. 10->12->2 
2. 10->4->18->22 
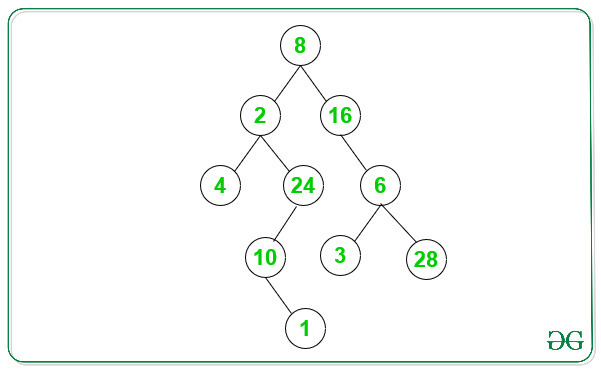
3. 10->4->18->24

Entrada: A continuación se muestra el árbol binario dado: 

Salida: 2 
Explicación: 
Hay 2 rutas pares para el árbol binario anterior: 
1. 8->2->4 
2. 8->16->6->28

Enfoque ingenuo: la idea es generar toda la ruta de la raíz a la hoja y verificar si todos los Nodes en cada ruta son pares o no. Cuente todos los caminos con Nodes pares y devuelva el conteo. La implementación anterior requiere espacio adicional para almacenar la ruta.

Enfoque eficiente: la idea es usar Preorder Tree Traversal . Durante el recorrido previo al pedido del árbol binario dado, haga lo siguiente: 

1. Si el valor actual del Node es impar o el puntero se convierte en NULL , devuelva el recuento.
2. Si el Node actual es un Node hoja, incremente el conteo en 1.
3. Llame recursivamente al subárbol izquierdo y derecho con el recuento actualizado.
4. Después de las llamadas totalmente recursivas, el valor de count es el número de caminos pares para un árbol binario dado.

A continuación se muestra la implementación del enfoque anterior:  

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// A Tree node
struct Node {
    int key;
    struct Node *left, *right;
};
 
// Utility function to create a new node
Node* newNode(int key)
{
    Node* temp = new Node;
    temp->key = key;
    temp->left = temp->right = NULL;
    return (temp);
}
 
// Utility function to count the even path
// in a given Binary tree
int evenPaths(struct Node* node, int count)
{
 
    // Base Condition, when node pointer
    // becomes null or node value is odd
    if (node == NULL || (node->key % 2 != 0)) {
        return count;
    }
 
    // Increment count when encounter leaf
    // node with all node value even
    if (!node->left && !node->right) {
        count++;
    }
 
    // Left recursive call, and save the
    // value of count
    count = evenPaths(node->left, count);
 
    // Right recursive call, and return
    // value of count
    return evenPaths(node->right, count);
}
 
// Function to count the even paths in a
// given Binary tree
int countEvenPaths(struct Node* node)
{
 
    // Function call with count = 0
    return evenPaths(node, 0);
}
 
// Driver Code
int main()
{
 
    // Tree
    Node* root = newNode(12);
    root->left = newNode(13);
    root->right = newNode(12);
 
    root->right->left = newNode(14);
    root->right->right = newNode(16);
 
    root->right->left->left = newNode(21);
    root->right->left->right = newNode(22);
    root->right->right->left = newNode(22);
    root->right->right->right = newNode(24);
    root->right->right->right->left = newNode(8);
 
    // Function call
    cout << countEvenPaths(root);
    return 0;
}

// Java program for the above approach
import java.util.*;
class GFG{
 
    // A Tree node
    static class Node {
        int key;
        Node left, right;
    };
     
    // Utility function to create a new node
    static Node newNode(int key)
    {
        Node temp = new Node();
        temp.key = key;
        temp.left = temp.right = null;
        return (temp);
    }
     
    // Utility function to count the even path
    // in a given Binary tree
    static int evenPaths(Node node, int count)
    {
     
        // Base Condition, when node pointer
        // becomes null or node value is odd
        if (node == null || (node.key % 2 != 0)) {
            return count;
        }
     
        // Increment count when encounter leaf
        // node with all node value even
        if (node.left == null && node.right == null) {
            count++;
        }
     
        // Left recursive call, and save the
        // value of count
        count = evenPaths(node.left, count);
     
        // Right recursive call, and return
        // value of count
        return evenPaths(node.right, count);
    }
     
    // Function to count the even paths in a
    // given Binary tree
    static int countEvenPaths(Node node)
    {
     
        // Function call with count = 0
        return evenPaths(node, 0);
    }
     
    // Driver Code
    public static void main(String args[])
    {
     
        // Tree
        Node root = newNode(12);
        root.left = newNode(13);
        root.right = newNode(12);
     
        root.right.left = newNode(14);
        root.right.right = newNode(16);
     
        root.right.left.left = newNode(21);
        root.right.left.right = newNode(22);
        root.right.right.left = newNode(22);
        root.right.right.right = newNode(24);
        root.right.right.right.left = newNode(8);
     
        // Function call
        System.out.println(countEvenPaths(root));
         
    }
}
 
// This code is contributed by AbhiThakur

# Python3 program for the
# above approach
 
 
# A Tree node
class Node:
   
    def __init__(self, x):
       
        self.key = x
        self.left = None
        self.right = None
 
# Utility function to count
# the even path in a given
# Binary tree
def evenPaths(node, count):
   
    # Base Condition, when node
    # pointer becomes null or
    # node value is odd
    if (node == None or
       (node.key % 2 != 0)):
        return count
 
    # Increment count when
    # encounter leaf node
    # with all node value even
    if (not node.left and
        not node.right):
        count+=1
 
    # Left recursive call, and
    # save the value of count
    count = evenPaths(node.left,
                      count)
 
    # Right recursive call, and
    # return value of count
    return evenPaths(node.right,
                     count)
 
# Function to count the even
# paths in a given Binary tree
def countEvenPaths(node):
   
    # Function call with count = 0
    return evenPaths(node, 0)
 
# Driver Code
if __name__ == '__main__':
 
    #Tree
    root = Node(12)
    root.left = Node(13)
    root.right = Node(12)
 
    root.right.left = Node(14)
    root.right.right = Node(16)
 
    root.right.left.left = Node(21)
    root.right.left.right = Node(22)
    root.right.right.left = Node(22)
    root.right.right.right = Node(24)
    root.right.right.right.left = Node(8)
 
    #Function call
    print(countEvenPaths(root))
 
# This code is contributed by Mohit Kumar 29

// C# program for the above approach
using System;
 
class GFG{
  
    // A Tree node
    class Node {
        public int key;
        public Node left, right;
    };
      
    // Utility function to create a new node
    static Node newNode(int key)
    {
        Node temp = new Node();
        temp.key = key;
        temp.left = temp.right = null;
        return (temp);
    }
      
    // Utility function to count the even path
    // in a given Binary tree
    static int evenPaths(Node node, int count)
    {
      
        // Base Condition, when node pointer
        // becomes null or node value is odd
        if (node == null || (node.key % 2 != 0)) {
            return count;
        }
      
        // Increment count when encounter leaf
        // node with all node value even
        if (node.left == null && node.right == null) {
            count++;
        }
      
        // Left recursive call, and save the
        // value of count
        count = evenPaths(node.left, count);
      
        // Right recursive call, and return
        // value of count
        return evenPaths(node.right, count);
    }
      
    // Function to count the even paths in a
    // given Binary tree
    static int countEvenPaths(Node node)
    {
      
        // Function call with count = 0
        return evenPaths(node, 0);
    }
      
    // Driver Code
    public static void Main(String []args)
    {
      
        // Tree
        Node root = newNode(12);
        root.left = newNode(13);
        root.right = newNode(12);
      
        root.right.left = newNode(14);
        root.right.right = newNode(16);
      
        root.right.left.left = newNode(21);
        root.right.left.right = newNode(22);
        root.right.right.left = newNode(22);
        root.right.right.right = newNode(24);
        root.right.right.right.left = newNode(8);
      
        // Function call
        Console.WriteLine(countEvenPaths(root));
          
    }
}
 
// This code is contributed by PrinciRaj1992

<script>
 
// Javascript program for the above approach
 
// A Tree node
class Node
{
     
    // Utility function to create
    // a new node
    constructor(key)
    {
        this.key = key;
        this.left = this.right = null;
    }
}
 
// Utility function to count the even path
// in a given Binary tree
function evenPaths(node, count)
{
     
    // Base Condition, when node pointer
    // becomes null or node value is odd
    if (node == null || (node.key % 2 != 0))
    {
        return count;
    }
  
    // Increment count when encounter leaf
    // node with all node value even
    if (node.left == null && node.right == null)
    {
        count++;
    }
  
    // Left recursive call, and save the
    // value of count
    count = evenPaths(node.left, count);
  
    // Right recursive call, and return
    // value of count
    return evenPaths(node.right, count);
}
 
// Function to count the even paths in a
// given Binary tree
function countEvenPaths(node)
{
     
    // Function call with count = 0
    return evenPaths(node, 0);
}
 
// Driver Code
let root = new Node(12);
root.left = new Node(13);
root.right = new Node(12);
 
root.right.left = new Node(14);
root.right.right = new Node(16);
 
root.right.left.left = new Node(21);
root.right.left.right = new Node(22);
root.right.right.left = new Node(22);
root.right.right.right = new Node(24);
root.right.right.right.left = new Node(8);
 
// Function call
document.write(countEvenPaths(root));
 
// This code is contributed by unknown2108
 
</script>

3

Complejidad de tiempo: O(N), donde N es el número de Nodes en el árbol binario dado.