Dadas dos strings S y T, encuentre el conteo de ocurrencias distintas de T en S como una subsecuencia.
Ejemplos:
Input: S = banana, T = ban Output: 3 Explanation: T appears in S as below three subsequences. [ban], [ba n], [b an] Input: S = geeksforgeeks, T = ge Output: 6 Explanation: T appears in S as below three subsequences. [ge], [ ge], [g e], [g e] [g e] and [ g e]
Enfoque: Cree una función recursiva tal que devuelva el recuento de subsecuencias de S que coincidan con T . Aquí m es la longitud de T y n es la longitud de S. Este problema se puede definir recursivamente como se muestra a continuación.
- Dado que la string T es una string vacía, devolver 1 como una string vacía puede ser la subsecuencia de todos.
- Dado que la string S es una string vacía, devolver 0 como ninguna string puede ser la subsecuencia de una string vacía.
- Si el último carácter de S y T no coincide, elimine el último carácter de S y vuelva a llamar a la función recursiva. Porque el último carácter de S no puede ser parte de la subsecuencia o eliminarlo y buscar otros caracteres.
- Si el último carácter de S coincide, entonces puede haber dos posibilidades, primero puede haber una subsecuencia donde el último carácter de S es parte de ella y segundo donde no es parte de la subsecuencia. Entonces el valor requerido será la suma de ambos. Llame a la función recursiva una vez con el último carácter de ambas strings eliminado y nuevamente con solo el último carácter de S eliminado.
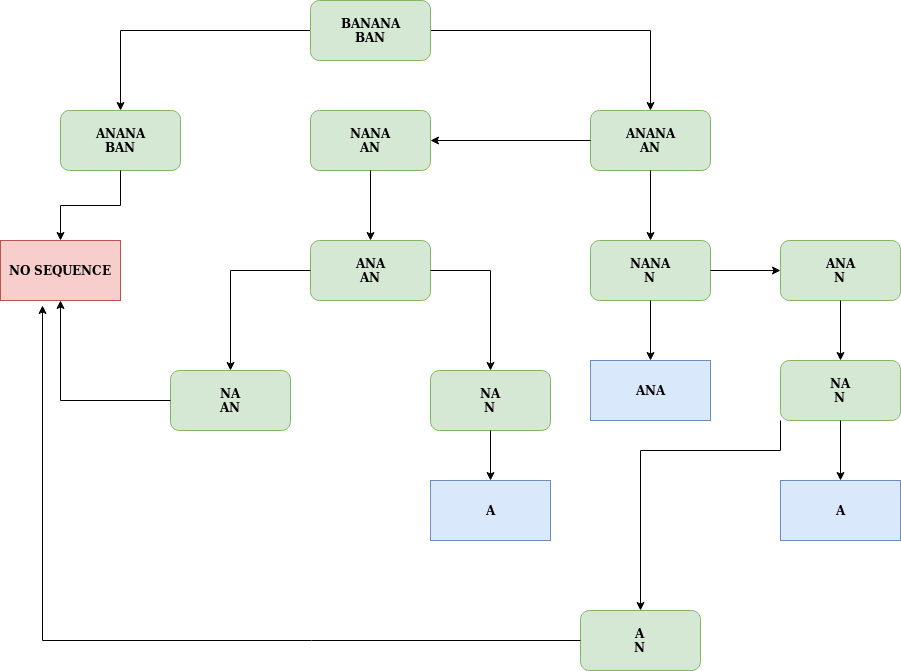
Los rectángulos redondos azules representan estados aceptados o hay una subsecuencia y los rectángulos redondos rojos representan No se puede formar una subsecuencia.
Implementación del enfoque recursivo:
C++
/* C/C++ program to count number of times S appears
as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;
int f(int i, int j, string s, string t)
{
if (j >= t.size()) {
return 1;
}
if (i >= s.size()) {
return 0;
}
if (s[i] == t[j]) {
return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);
}
return f(i + 1, j, s, t);
}
int findSubsequenceCount(string s, string t)
{
return f(0, 0, s, t);
}
// Driver code to check above method
int main()
{
string T = "ge";
string S = "geeksforgeeks";
cout << findSubsequenceCount(S, T) << endl;
return 0;
}
Java
// Java program to count number of times
// S appears as a subsequence in T
import java.io.*;
class GFG {
static int f(int i, int j, String s,
String t)
{
// base case
// if second string completed then we found the
// matching pattern
if (j >= t.length()) {
return 1;
}
// if first string is completed we can not find any
// matching pattern.
if (i >= s.length()) {
return 0;
}
// if character at i'th place is equal to character
// at j'th place then
// we can either take it or not take it.
if (s.charAt(i) == t.charAt(j)) {
return f(i + 1, j + 1, s, t)
+ f(i + 1, j, s, t);
}
// if characters are not equal then we will increase
// only first string
return f(i + 1, j, s, t);
}
// Driver code to check above method
public static void main(String[] args)
{
String T = "ge";
String S = "geeksforgeeks";
System.out.println(
f(0, 0, S, T));
}
}
// This code is contributed by Sanskar.
C#
/* C# program to count number of times S appears
as a subsequence in T */
using System;
class GFG {
static int f(int i, int j, string s, string t)
{
if (j >= t.Length) {
return 1;
}
if (i >= s.Length) {
return 0;
}
if (s[i] == t[j]) {
return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);
}
return f(i + 1, j, s, t);
}
static int findSubsequenceCount(string s, string t)
{
return f(0, 0, s, t);
}
// Driver code to check above method
public static void Main()
{
string T = "ge";
string S = "geeksforgeeks";
Console.WriteLine(findSubsequenceCount(S, T));
}
}
// This code contributed by Pushpesh Raj.
Javascript
<script>
// Javascript program to count number of times S appears
// as a subsequence in T
function f(i, j, s, t) {
if (j >= t.length) {
return 1;
}
if (i >= s.length) {
return 0;
}
if (s[i] == t[j]) {
return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);
}
return f(i + 1, j, s, t);
}
function findSubsequenceCount(s, t) {
return f(0, 0, s, t);
}
// Driver code to check above method
let T = "ge";
let S = "geeksforgeeks";
document.write(findSubsequenceCount(S, T))
</script>
6
Dado que hay subproblemas superpuestos en el resultado de recurrencia anterior, se puede aplicar el enfoque de programación dinámica para resolver el problema anterior. Almacene los subproblemas en un Hashmap o una array y devuelva el valor cuando se vuelva a llamar a la función.
Algoritmo:
- Cree una array 2D mat[m+1][n+1] donde m es la longitud de la string T y n es la longitud de la string S. mat[i][j] denota el número de subsecuencias distintas de la substring S(1.. i) y la substring T(1..j) por lo que mat[m][n] contiene nuestra solución.
- Inicialice la primera columna con todos los 0. Una string vacía no puede tener otra string como subsecuencia
- Inicialice la primera fila con todos los 1. Una string vacía es una subsecuencia de todos.
- Rellene la array de forma ascendente, es decir, todos los subproblemas de la string actual se calculan primero.
- Recorre la cuerda T de principio a fin. (el contador es yo )
- Para cada iteración del bucle exterior, atraviesa la string S de principio a fin. (el contador es j )
- Si el carácter en el i -ésimo índice de la string T coincide con el j -ésimo carácter de la string S , el valor se obtiene considerando dos casos. Primero, son todas las substrings sin el último carácter en S y segundo son las substrings sin los últimos caracteres en ambos, es decir, mat[i+1][j] + mat[i][j] .
- De lo contrario, el valor será el mismo incluso si se elimina el j -ésimo carácter de S , es decir, mat[i+1][j]
- Imprime el valor de mat[m-1][n-1] como respuesta.
C++
/* C/C++ program to count number of times S appears
as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;
int findSubsequenceCount(string S, string T)
{
int m = T.length(), n = S.length();
// T can't appear as a subsequence in S
if (m > n)
return 0;
// mat[i][j] stores the count of occurrences of
// T(1..i) in S(1..j).
int mat[m + 1][n + 1];
// Initializing first column with all 0s. An empty
// string can't have another string as subsequence
for (int i = 1; i <= m; i++)
mat[i][0] = 0;
// Initializing first row with all 1s. An empty
// string is subsequence of all.
for (int j = 0; j <= n; j++)
mat[0][j] = 1;
// Fill mat[][] in bottom up manner
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If last characters don't match, then value
// is same as the value without last character
// in S.
if (T[i - 1] != S[j - 1])
mat[i][j] = mat[i][j - 1];
// Else value is obtained considering two cases.
// a) All substrings without last character in S
// b) All substrings without last characters in
// both.
else
mat[i][j] = mat[i][j - 1] + mat[i - 1][j - 1];
}
}
/* uncomment this to print matrix mat
for (int i = 1; i <= m; i++, cout << endl)
for (int j = 1; j <= n; j++)
cout << mat[i][j] << " "; */
return mat[m][n];
}
// Driver code to check above method
int main()
{
string T = "ge";
string S = "geeksforgeeks";
cout << findSubsequenceCount(S, T) << endl;
return 0;
}
Java
// Java program to count number of times
// S appears as a subsequence in T
import java.io.*;
class GFG {
static int findSubsequenceCount(String S, String T)
{
int m = T.length();
int n = S.length();
// T can't appear as a subsequence in S
if (m > n)
return 0;
// mat[i][j] stores the count of
// occurrences of T(1..i) in S(1..j).
int mat[][] = new int[m + 1][n + 1];
// Initializing first column with
// all 0s. An emptystring can't have
// another string as subsequence
for (int i = 1; i <= m; i++)
mat[i][0] = 0;
// Initializing first row with all 1s.
// An empty string is subsequence of all.
for (int j = 0; j <= n; j++)
mat[0][j] = 1;
// Fill mat[][] in bottom up manner
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If last characters don't match,
// then value is same as the value
// without last character in S.
if (T.charAt(i - 1) != S.charAt(j - 1))
mat[i][j] = mat[i][j - 1];
// Else value is obtained considering two cases.
// a) All substrings without last character in S
// b) All substrings without last characters in
// both.
else
mat[i][j] = mat[i][j - 1] + mat[i - 1][j - 1];
}
}
/* uncomment this to print matrix mat
for (int i = 1; i <= m; i++, cout << endl)
for (int j = 1; j <= n; j++)
System.out.println ( mat[i][j] +" "); */
return mat[m][n];
}
// Driver code to check above method
public static void main(String[] args)
{
String T = "ge";
String S = "geeksforgeeks";
System.out.println(findSubsequenceCount(S, T));
}
}
// This code is contributed by vt_m
Python3
# Python3 program to count number of times # S appears as a subsequence in T def findSubsequenceCount(S, T): m = len(T) n = len(S) # T can't appear as a subsequence in S if m > n: return 0 # mat[i][j] stores the count of # occurrences of T(1..i) in S(1..j). mat = [[0 for _ in range(n + 1)] for __ in range(m + 1)] # Initializing first column with all 0s. x # An empty string can't have another # string as subsequence for i in range(1, m + 1): mat[i][0] = 0 # Initializing first row with all 1s. # An empty string is subsequence of all. for j in range(n + 1): mat[0][j] = 1 # Fill mat[][] in bottom up manner for i in range(1, m + 1): for j in range(1, n + 1): # If last characters don't match, # then value is same as the value # without last character in S. if T[i - 1] != S[j - 1]: mat[i][j] = mat[i][j - 1] # Else value is obtained considering two cases. # a) All substrings without last character in S # b) All substrings without last characters in # both. else: mat[i][j] = (mat[i][j - 1] + mat[i - 1][j - 1]) return mat[m][n] # Driver Code if __name__ == "__main__": T = "ge" S = "geeksforgeeks" print(findSubsequenceCount(S, T)) # This code is contributed # by vibhu4agarwal
C#
// C# program to count number of times
// S appears as a subsequence in T
using System;
class GFG {
static int findSubsequenceCount(string S, string T)
{
int m = T.Length;
int n = S.Length;
// T can't appear as a subsequence in S
if (m > n)
return 0;
// mat[i][j] stores the count of
// occurrences of T(1..i) in S(1..j).
int[, ] mat = new int[m + 1, n + 1];
// Initializing first column with
// all 0s. An emptystring can't have
// another string as subsequence
for (int i = 1; i <= m; i++)
mat[i, 0] = 0;
// Initializing first row with all 1s.
// An empty string is subsequence of all.
for (int j = 0; j <= n; j++)
mat[0, j] = 1;
// Fill mat[][] in bottom up manner
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// If last characters don't match,
// then value is same as the value
// without last character in S.
if (T[i - 1] != S[j - 1])
mat[i, j] = mat[i, j - 1];
// Else value is obtained considering two cases.
// a) All substrings without last character in S
// b) All substrings without last characters in
// both.
else
mat[i, j] = mat[i, j - 1] + mat[i - 1, j - 1];
}
}
/* uncomment this to print matrix mat
for (int i = 1; i <= m; i++, cout << endl)
for (int j = 1; j <= n; j++)
System.out.println ( mat[i][j] +" "); */
return mat[m, n];
}
// Driver code to check above method
public static void Main()
{
string T = "ge";
string S = "geeksforgeeks";
Console.WriteLine(findSubsequenceCount(S, T));
}
}
// This code is contributed by vt_m
PHP
<?php
// PHP program to count number of times
// S appears as a subsequence in T */
function findSubsequenceCount($S, $T)
{
$m = strlen($T); $n = strlen($S);
// T can't appear as a subsequence in S
if ($m > $n)
return 0;
// mat[i][j] stores the count of
// occurrences of T(1..i) in S(1..j).
$mat = array(array());
// Initializing first column with all 0s.
// An empty string can't have another
// string as subsequence
for ($i = 1; $i <= $m; $i++)
$mat[$i][0] = 0;
// Initializing first row with all 1s.
// An empty string is subsequence of all.
for ($j = 0; $j <= $n; $j++)
$mat[0][$j] = 1;
// Fill mat[][] in bottom up manner
for ($i = 1; $i <= $m; $i++)
{
for ($j = 1; $j <= $n; $j++)
{
// If last characters don't match,
// then value is same as the value
// without last character in S.
if ($T[$i - 1] != $S[$j - 1])
$mat[$i][$j] = $mat[$i][$j - 1];
// Else value is obtained considering two cases.
// a) All substrings without last character in S
// b) All substrings without last characters in
// both.
else
$mat[$i][$j] = $mat[$i][$j - 1] +
$mat[$i - 1][$j - 1];
}
}
/* uncomment this to print matrix mat
for (int i = 1; i <= m; i++, cout << endl)
for (int j = 1; j <= n; j++)
cout << mat[i][j] << " "; */
return $mat[$m][$n];
}
// Driver Code
$T = "ge";
$S = "geeksforgeeks";
echo findSubsequenceCount($S, $T) . "\n";
// This code is contributed
// by Akanksha Rai
Javascript
<script>
// JavaScript program to count number of times
// S appears as a subsequence in T
function findSubsequenceCount(S, T)
{
let m = T.length;
let n = S.length;
// T can't appear as a subsequence in S
if (m > n)
return 0;
// mat[i][j] stores the count of
// occurrences of T(1..i) in S(1..j).
let mat = new Array(m + 1);
for (let i = 0; i <= m; i++)
{
mat[i] = new Array(n + 1);
for (let j = 0; j <= n; j++)
{
mat[i][j] = 0;
}
}
// Initializing first column with
// all 0s. An emptystring can't have
// another string as subsequence
for (let i = 1; i <= m; i++)
mat[i][0] = 0;
// Initializing first row with all 1s.
// An empty string is subsequence of all.
for (let j = 0; j <= n; j++)
mat[0][j] = 1;
// Fill mat[][] in bottom up manner
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// If last characters don't match,
// then value is same as the value
// without last character in S.
if (T[i - 1] != S[j - 1])
mat[i][j] = mat[i][j - 1];
// Else value is obtained
// considering two cases.
// a) All substrings without
// last character in S
// b) All substrings without
// last characters in
// both.
else
mat[i][j] = mat[i][j - 1] +
mat[i - 1][j - 1];
}
}
/* uncomment this to print matrix mat
for (int i = 1; i <= m; i++, cout << endl)
for (int j = 1; j <= n; j++)
System.out.println ( mat[i][j] +" "); */
return mat[m][n];
}
let T = "ge";
let S = "geeksforgeeks";
document.write(findSubsequenceCount(S, T));
</script>
6
Análisis de Complejidad:
- Complejidad temporal: O(m*n).
Solo se necesita un recorrido de la array, por lo que la complejidad del tiempo es O (m * n) - Espacio Auxiliar: O(m*n).
Se necesita una array de tamaño m*n para que la complejidad del espacio sea O(m*n).
Nota: Dado que mat[i][j] accede a elementos de la fila actual y de la fila anterior únicamente, podemos optimizar el espacio auxiliar simplemente usando dos filas reduciendo el espacio de m*n a 2*n.
Otra forma de resolver la programación dinámica es mediante el enfoque de arriba hacia abajo mediante la memorización.
A continuación se muestra el código:
C++
/* C/C++ program to count number of times S appears
as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;
int f(int i, int j, string s, string t,
vector<vector<int> >& dp)
{
if (t.size() - j > s.size() - i)
return 0;
if (j == t.size()) {
return 1;
}
if (i == s.size()) {
return 0;
}
if (dp[i][j] != -1) {
return dp[i][j];
}
if (s[i] == t[j]) {
return dp[i][j] = f(i + 1, j + 1, s, t, dp)
+ f(i + 1, j, s, t, dp);
}
return dp[i][j] = f(i + 1, j, s, t, dp);
}
int findSubsequenceCount(string s, string t)
{
vector<vector<int> > dp(s.size(),
vector<int>(t.size(), -1));
return f(0, 0, s, t, dp);
}
// Driver code to check above method
int main()
{
string T = "ge";
string S = "geeksforgeeks";
cout << findSubsequenceCount(S, T) << endl;
return 0;
}
6
Análisis de Complejidad:
- Complejidad temporal: O(m*n). Solo se necesita un recorrido de la array, por lo que la complejidad del tiempo es O (m * n)
- Espacio auxiliar: O(m*n) ignorando el espacio de la pila de recursividad
Este artículo es una contribución de Utkarsh Trivedi . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA