Dado un laberinto con obstáculos, cuente el número de caminos para llegar a la celda más a la derecha e inferior desde la celda más a la izquierda. Una celda en el laberinto dado tiene un valor de -1 si es un bloqueo o callejón sin salida, de lo contrario 0.
Desde una celda dada, podemos movernos a las celdas (i+1, j) y (i, j+1) solamente.
Ejemplos:
Input: maze[R][C] = {{0, 0, 0, 0},
{0, -1, 0, 0},
{-1, 0, 0, 0},
{0, 0, 0, 0}};
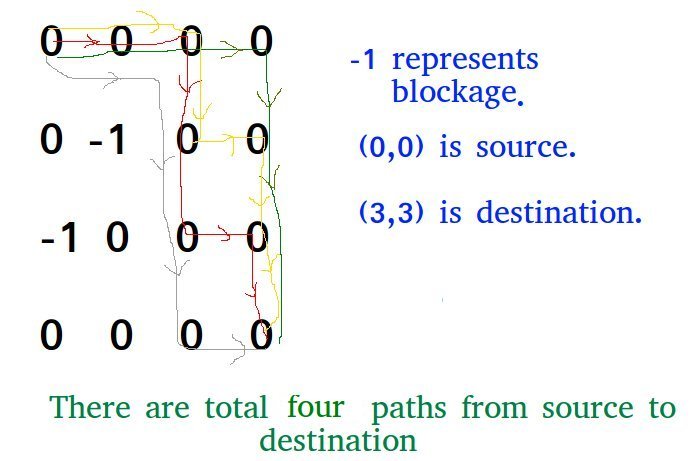
Output: 4
There are four possible paths as shown in
below diagram.
Este problema es una extensión del siguiente problema.
Retrocediendo | Conjunto 2 (Rata en un laberinto)
En esta publicación, se analiza una solución diferente que también se puede usar para resolver el problema anterior de Rat in a Maze.
La idea es modificar la grilla[][] dada para que la grilla[i][j] contenga el número de rutas para llegar a (i, j) desde (0, 0) si (i, j) no es un bloqueo, de lo contrario grid[i][j] sigue siendo -1.
We can recursively compute grid[i][j] using below
formula and finally return grid[R-1][C-1]
// If current cell is a blockage
if (maze[i][j] == -1)
maze[i][j] = -1; // Do not change
// If we can reach maze[i][j] from maze[i-1][j]
// then increment count.
else if (maze[i-1][j] > 0)
maze[i][j] = (maze[i][j] + maze[i-1][j]);
// If we can reach maze[i][j] from maze[i][j-1]
// then increment count.
else if (maze[i][j-1] > 0)
maze[i][j] = (maze[i][j] + maze[i][j-1]);
A continuación se muestra la implementación de la idea anterior.
C++
// C++ program to count number of paths in a maze
// with obstacles.
#include<bits/stdc++.h>
using namespace std;
#define R 4
#define C 4
// Returns count of possible paths in a maze[R][C]
// from (0,0) to (R-1,C-1)
int countPaths(int maze[][C])
{
// If the initial cell is blocked, there is no
// way of moving anywhere
if (maze[0][0]==-1)
return 0;
// Initializing the leftmost column
for (int i=0; i<R; i++)
{
if (maze[i][0] == 0)
maze[i][0] = 1;
// If we encounter a blocked cell in leftmost
// row, there is no way of visiting any cell
// directly below it.
else
break;
}
// Similarly initialize the topmost row
for (int i=1; i<C; i++)
{
if (maze[0][i] == 0)
maze[0][i] = 1;
// If we encounter a blocked cell in bottommost
// row, there is no way of visiting any cell
// directly below it.
else
break;
}
// The only difference is that if a cell is -1,
// simply ignore it else recursively compute
// count value maze[i][j]
for (int i=1; i<R; i++)
{
for (int j=1; j<C; j++)
{
// If blockage is found, ignore this cell
if (maze[i][j] == -1)
continue;
// If we can reach maze[i][j] from maze[i-1][j]
// then increment count.
if (maze[i-1][j] > 0)
maze[i][j] = (maze[i][j] + maze[i-1][j]);
// If we can reach maze[i][j] from maze[i][j-1]
// then increment count.
if (maze[i][j-1] > 0)
maze[i][j] = (maze[i][j] + maze[i][j-1]);
}
}
// If the final cell is blocked, output 0, otherwise
// the answer
return (maze[R-1][C-1] > 0)? maze[R-1][C-1] : 0;
}
// Driver code
int main()
{
int maze[R][C] = {{0, 0, 0, 0},
{0, -1, 0, 0},
{-1, 0, 0, 0},
{0, 0, 0, 0}};
cout << countPaths(maze);
return 0;
}
Java
// Java program to count number of paths in a maze
// with obstacles.
import java.io.*;
class GFG
{
static int R = 4;
static int C = 4;
// Returns count of possible paths in
// a maze[R][C] from (0,0) to (R-1,C-1)
static int countPaths(int maze[][])
{
// If the initial cell is blocked,
// there is no way of moving anywhere
if (maze[0][0]==-1)
return 0;
// Initializing the leftmost column
for (int i = 0; i < R; i++)
{
if (maze[i][0] == 0)
maze[i][0] = 1;
// If we encounter a blocked cell
// in leftmost row, there is no way
// of visiting any cell directly below it.
else
break;
}
// Similarly initialize the topmost row
for (int i =1 ; i< C ; i++)
{
if (maze[0][i] == 0)
maze[0][i] = 1;
// If we encounter a blocked cell in
// bottommost row, there is no way of
// visiting any cell directly below it.
else
break;
}
// The only difference is that if a cell
// is -1, simply ignore it else recursively
// compute count value maze[i][j]
for (int i = 1; i < R; i++)
{
for (int j = 1; j <C ; j++)
{
// If blockage is found,
// ignore this cell
if (maze[i][j] == -1)
continue;
// If we can reach maze[i][j] from
// maze[i-1][j] then increment count.
if (maze[i - 1][j] > 0)
maze[i][j] = (maze[i][j] +
maze[i - 1][j]);
// If we can reach maze[i][j] from
// maze[i][j-1] then increment count.
if (maze[i][j - 1] > 0)
maze[i][j] = (maze[i][j] +
maze[i][j - 1]);
}
}
// If the final cell is blocked,
// output 0, otherwise the answer
return (maze[R - 1][C - 1] > 0) ?
maze[R - 1][C - 1] : 0;
}
// Driver code
public static void main (String[] args)
{
int maze[][] = {{0, 0, 0, 0},
{0, -1, 0, 0},
{-1, 0, 0, 0},
{0, 0, 0, 0}};
System.out.println (countPaths(maze));
}
}
// This code is contributed by vt_m
Python3
# Python 3 program to count number of paths # in a maze with obstacles. R = 4 C = 4 # Returns count of possible paths in a # maze[R][C] from (0,0) to (R-1,C-1) def countPaths(maze): # If the initial cell is blocked, # there is no way of moving anywhere if (maze[0][0] == -1): return 0 # Initializing the leftmost column for i in range(R): if (maze[i][0] == 0): maze[i][0] = 1 # If we encounter a blocked cell in # leftmost row, there is no way of # visiting any cell directly below it. else: break # Similarly initialize the topmost row for i in range(1, C, 1): if (maze[0][i] == 0): maze[0][i] = 1 # If we encounter a blocked cell in # bottommost row, there is no way of # visiting any cell directly below it. else: break # The only difference is that if a cell is -1, # simply ignore it else recursively compute # count value maze[i][j] for i in range(1, R, 1): for j in range(1, C, 1): # If blockage is found, ignore this cell if (maze[i][j] == -1): continue # If we can reach maze[i][j] from # maze[i-1][j] then increment count. if (maze[i - 1][j] > 0): maze[i][j] = (maze[i][j] + maze[i - 1][j]) # If we can reach maze[i][j] from # maze[i][j-1] then increment count. if (maze[i][j - 1] > 0): maze[i][j] = (maze[i][j] + maze[i][j - 1]) # If the final cell is blocked, # output 0, otherwise the answer if (maze[R - 1][C - 1] > 0): return maze[R - 1][C - 1] else: return 0 # Driver code if __name__ == '__main__': maze = [[0, 0, 0, 0], [0, -1, 0, 0], [-1, 0, 0, 0], [0, 0, 0, 0 ]] print(countPaths(maze)) # This code is contributed by # Surendra_Gangwar
C#
// C# program to count number of paths in a maze
// with obstacles.
using System;
class GFG {
static int R = 4;
static int C = 4;
// Returns count of possible paths in
// a maze[R][C] from (0,0) to (R-1,C-1)
static int countPaths(int [,]maze)
{
// If the initial cell is blocked,
// there is no way of moving anywhere
if (maze[0,0]==-1)
return 0;
// Initializing the leftmost column
for (int i = 0; i < R; i++)
{
if (maze[i,0] == 0)
maze[i,0] = 1;
// If we encounter a blocked cell
// in leftmost row, there is no way
// of visiting any cell directly below it.
else
break;
}
// Similarly initialize the topmost row
for (int i =1 ; i< C ; i++)
{
if (maze[0,i] == 0)
maze[0,i] = 1;
// If we encounter a blocked cell in
// bottommost row, there is no way of
// visiting any cell directly below it.
else
break;
}
// The only difference is that if a cell
// is -1, simply ignore it else recursively
// compute count value maze[i][j]
for (int i = 1; i < R; i++)
{
for (int j = 1; j <C ; j++)
{
// If blockage is found,
// ignore this cell
if (maze[i,j] == -1)
continue;
// If we can reach maze[i][j] from
// maze[i-1][j] then increment count.
if (maze[i - 1,j] > 0)
maze[i,j] = (maze[i,j] +
maze[i - 1,j]);
// If we can reach maze[i][j] from
// maze[i][j-1] then increment count.
if (maze[i,j - 1] > 0)
maze[i,j] = (maze[i,j] +
maze[i,j - 1]);
}
}
// If the final cell is blocked,
// output 0, otherwise the answer
return (maze[R - 1,C - 1] > 0) ?
maze[R - 1,C - 1] : 0;
}
// Driver code
public static void Main ()
{
int [,]maze = { {0, 0, 0, 0},
{0, -1, 0, 0},
{-1, 0, 0, 0},
{0, 0, 0, 0}};
Console.Write (countPaths(maze));
}
}
// This code is contributed by nitin mittal.
PHP
<?php
// PHP program to count number
// of paths in a maze with obstacles.
$R = 4;
$C = 4;
// Returns count of possible
// paths in a maze[R][C]
// from (0,0) to (R-1,C-1)
function countPaths( $maze)
{
global $R, $C;
// If the initial cell is
// blocked, there is no
// way of moving anywhere
if ($maze[0][0] == - 1)
return 0;
// Initializing the
// leftmost column
for ( $i = 0; $i < $R; $i++)
{
if ($maze[$i][0] == 0)
$maze[$i][0] = 1;
// If we encounter a blocked
// cell in leftmost row,
// there is no way of
// visiting any cell
// directly below it.
else
break;
}
// Similarly initialize
// the topmost row
for($i = 1; $i < $C; $i++)
{
if ($maze[0][$i] == 0)
$maze[0][$i] = 1;
// If we encounter a blocked
// cell in bottommost row,
// there is no way of
// visiting any cell
// directly below it.
else
break;
}
// The only difference is
// that if a cell is -1,
// simply ignore it else
// recursively compute
// count value maze[i][j]
for($i = 1; $i < $R; $i++)
{
for($j = 1; $j < $C; $j++)
{
// If blockage is found,
// ignore this cell
if ($maze[$i][$j] == -1)
continue;
// If we can reach maze[i][j]
// from maze[i-1][j]
// then increment count.
if ($maze[$i - 1][$j] > 0)
$maze[$i][$j] = ($maze[$i][$j] +
$maze[$i - 1][$j]);
// If we can reach maze[i][j]
// from maze[i][j-1]
// then increment count.
if ($maze[$i][$j - 1] > 0)
$maze[$i][$j] = ($maze[$i][$j] +
$maze[$i][$j - 1]);
}
}
// If the final cell is
// blocked, output 0,
// otherwise the answer
return ($maze[$R - 1][$C - 1] > 0) ?
$maze[$R - 1][$C - 1] : 0;
}
// Driver Code
$maze = array(array(0, 0, 0, 0),
array(0, -1, 0, 0),
array(-1, 0, 0, 0),
array(0, 0, 0, 0));
echo countPaths($maze);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// JavaScript program to count number
// of paths in a maze with obstacles.
let R = 4;
let C = 4;
// Returns count of possible paths in
// a maze[R][C] from (0,0) to (R-1,C-1)
function countPaths(maze)
{
// If the initial cell is blocked,
// there is no way of moving anywhere
if (maze[0][0] == -1)
return 0;
// Initializing the leftmost column
for(let i = 0; i < R; i++)
{
if (maze[i][0] == 0)
maze[i][0] = 1;
// If we encounter a blocked cell
// in leftmost row, there is no way
// of visiting any cell directly below it.
else
break;
}
// Similarly initialize the topmost row
for(let i = 1; i < C; i++)
{
if (maze[0][i] == 0)
maze[0][i] = 1;
// If we encounter a blocked cell in
// bottommost row, there is no way of
// visiting any cell directly below it.
else
break;
}
// The only difference is that if a cell
// is -1, simply ignore it else recursively
// compute count value maze[i][j]
for(let i = 1; i < R; i++)
{
for(let j = 1; j < C; j++)
{
// If blockage is found,
// ignore this cell
if (maze[i][j] == -1)
continue;
// If we can reach maze[i][j] from
// maze[i-1][j] then increment count.
if (maze[i - 1][j] > 0)
maze[i][j] = (maze[i][j] +
maze[i - 1][j]);
// If we can reach maze[i][j] from
// maze[i][j-1] then increment count.
if (maze[i][j - 1] > 0)
maze[i][j] = (maze[i][j] +
maze[i][j - 1]);
}
}
// If the final cell is blocked,
// output 0, otherwise the answer
return (maze[R - 1][C - 1] > 0) ?
maze[R - 1][C - 1] : 0;
}
// Driver Code
let maze = [ [ 0, 0, 0, 0 ],
[ 0, -1, 0, 0 ],
[ -1, 0, 0, 0 ],
[ 0, 0, 0, 0 ] ];
document.write(countPaths(maze));
// This code is contributed by code_hunt
</script>
4
Complejidad temporal: O(R x C)
Este artículo es una contribución de Roshni Agarwal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA