Cuente los pares de dos arrays cuya operación de módulo produzca K

Dado un entero $k$ y dos arrays $arr1$ y $arr2$ , la tarea es contar los pares totales (formados después de elegir un elemento de $arr1$ y otro de $arr2$ ) de estas arrays cuya operación de módulo da como resultado $k$ .
Nota: Si en un par (a, b) , a > b entonces el módulo debe realizarse como a % b . Además, los pares que ocurran más de una vez se contarán solo una vez.
Ejemplos:

Entrada: arr1[] = {1, 3, 7}, arr2[] = {5, 3, 1}, K = 2
Salida: 2
(3, 5) y (7, 5) son los únicos pares posibles.
Ya que, 5 % 3 = 2 y 7 % 5 = 2
Entrada: arr1[] = {2, 5, 99}, arr2[] = {2, 8, 1, 4}, K = 0
Salida: 6
Todos los pares posibles son (2, 2), (2, 8), (2, 4), (2, 1), (5, 1) y (99, 1).

Acercarse:

Tome un elemento de $arr1$ a la vez y realice su operación de módulo con todos los demás elementos de $arr2$ uno en uno.
Si el resultado del paso anterior es igual a 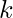$k$ entonces almacene el par (a, b) en un conjunto para evitar duplicados donde a es el elemento más pequeño yb es el más grande.
El total de pares requeridos será el tamaño del conjunto al final.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the total pairs
// of elements whose modulo yield K
int totalPairs(int arr1[], int arr2[], int K, int n, int m)
{
 
    // set is used to avoid duplicate pairs
    set<pair<int, int> > s;
 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
 
            // check which element is greater and
            // proceed according to it
            if (arr1[i] > arr2[j]) {
 
                // check if modulo is equal to K
                if (arr1[i] % arr2[j] == K)
                    s.insert(make_pair(arr1[i], arr2[j]));
            }
            else {
                if (arr2[j] % arr1[i] == K)
                    s.insert(make_pair(arr2[j], arr1[i]));
            }
        }
    }
 
    // return size of the set
    return s.size();
}
 
// Driver code
int main()
{
    int arr1[] = { 8, 3, 7, 50 };
    int arr2[] = { 5, 1, 10, 4 };
    int K = 3;
    int n = sizeof(arr1) / sizeof(arr1[0]);
    int m = sizeof(arr2) / sizeof(arr2[0]);
 
    cout << totalPairs(arr1, arr2, K, n, m);
    return 0;
}

Java

// Java implementation of above approach
import java.util.*;
 
class GFG
{
    static class pair
    {
        int first, second;
        public pair(int first, int second)
        {
            this.first = first;
            this.second = second;
        }
    }
     
    // Function to return the total pairs
    // of elements whose modulo yield K
    static int totalPairs(int []arr1, int []arr2,
                          int K, int n, int m)
    {
     
        // set is used to avoid duplicate pairs
        HashSet<pair> s = new HashSet<pair>();
     
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
     
                // check which element is greater and
                // proceed according to it
                if (arr1[i] > arr2[j])
                {
     
                    // check if modulo is equal to K
                    if (arr1[i] % arr2[j] == K)
                        s.add(new pair(arr1[i], arr2[j]));
                }
                else
                {
                    if (arr2[j] % arr1[i] == K)
                        s.add(new pair(arr2[j], arr1[i]));
                }
            }
        }
     
        // return size of the set
        return s.size();
    }
     
    // Driver code
    public static void main(String []args)
    {
        int []arr1 = { 8, 3, 7, 50 };
        int []arr2 = { 5, 1, 10, 4 };
        int K = 3;
        int n = arr1.length;
        int m = arr2.length;
     
        System.out.println(totalPairs(arr1, arr2, K, n, m));
    }
}
 
// This code is contributed by Princi Singh

Python3

# Python3 implementation of above approach
 
# Function to return the total pairs
# of elements whose modulo yield K
def totalPairs(arr1, arr2, K, n, m):
 
    # set is used to avoid duplicate pairs
    s={}
 
    for i in range(n):
        for j in range(m):
 
            # check which element is greater and
            # proceed according to it
            if (arr1[i] > arr2[j]):
 
                # check if modulo is equal to K
                if (arr1[i] % arr2[j] == K):
                    s[(arr1[i], arr2[j])]=1
            else:
                if (arr2[j] % arr1[i] == K):
                    s[(arr2[j], arr1[i])]=1
 
 
 
    # return size of the set
    return len(s)
 
# Driver code
 
arr1 = [ 8, 3, 7, 50 ]
arr2 = [5, 1, 10, 4 ]
K = 3
n = len(arr1)
m = len(arr2)
 
print(totalPairs(arr1, arr2, K, n, m))
 
# This code is contributed by mohit kumar 29

C#

// C# implementation of the approach
using System;
using System.Collections.Generic;
     
class GFG
{
    public class pair
    {
        public int first, second;
        public pair(int first, int second)
        {
            this.first = first;
            this.second = second;
        }
    }
     
    // Function to return the total pairs
    // of elements whose modulo yield K
    static int totalPairs(int []arr1, int []arr2,
                          int K, int n, int m)
    {
     
        // set is used to avoid duplicate pairs
        HashSet<pair> s = new HashSet<pair>();
     
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
     
                // check which element is greater and
                // proceed according to it
                if (arr1[i] > arr2[j])
                {
     
                    // check if modulo is equal to K
                    if (arr1[i] % arr2[j] == K)
                        s.Add(new pair(arr1[i], arr2[j]));
                }
                else
                {
                    if (arr2[j] % arr1[i] == K)
                        s.Add(new pair(arr2[j], arr1[i]));
                }
            }
        }
     
        // return size of the set
        return s.Count;
    }
     
    // Driver code
    public static void Main(String []args)
    {
        int []arr1 = { 8, 3, 7, 50 };
        int []arr2 = { 5, 1, 10, 4 };
        int K = 3;
        int n = arr1.Length;
        int m = arr2.Length;
     
        Console.WriteLine(totalPairs(arr1, arr2, K, n, m));
    }
}
 
// This code is contributed by PrinciRaj1992

Javascript

<script>
 
// Javascript implementation of above approach
 
// Function to return the total pairs
// of elements whose modulo yield K
function totalPairs(arr1, arr2, K, n, m)
{
 
    // set is used to avoid duplicate pairs
    var s = new Set();
 
    for (var i = 0; i < n; i++) {
        for (var j = 0; j < m; j++) {
 
            // check which element is greater and
            // proceed according to it
            if (arr1[i] > arr2[j]) {
 
                // check if modulo is equal to K
                if (arr1[i] % arr2[j] == K)
                    s.add([arr1[i], arr2[j]]);
            }
            else {
                if (arr2[j] % arr1[i] == K)
                    s.add([arr2[j], arr1[i]]);
            }
        }
    }
 
    // return size of the set
    return s.size;
}
 
// Driver code
var arr1 = [ 8, 3, 7, 50 ];
var arr2 = [ 5, 1, 10, 4 ];
var K = 3;
var n = arr1.length;
var m = arr2.length;
document.write( totalPairs(arr1, arr2, K, n, m));
 
</script>

Producción:

Complejidad temporal: O(n * m)

Espacio Auxiliar: O(n * m)

Nota: Para imprimir todos los pares solo imprima los elementos del conjunto.

Publicación traducida automáticamente

Artículo escrito por Shashank_Sharma y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta