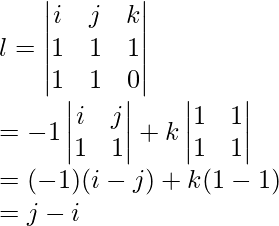La rotación de cuerpos rígidos ocupa un lugar destacado en la ciencia, los deportes y la ingeniería. Teóricamente, es un conjunto de partículas que se encuentran a una distancia fija unas de otras. En un escenario ideal, estos cuerpos no cambian de forma ni se deforman. Este tipo de cuerpos suelen ser una distribución continua de masa. Para analizar el movimiento de tales cuerpos, se requiere la posición del centro de masa. Cuando se aplican fuerzas a tales cuerpos, se produce una aceleración angular y una aceleración lineal. Se hace imprescindible estudiar cómo estas fuerzas afectan a los cuerpos rígidos y producen en ellos una aceleración angular y lineal. Veámoslos en detalle.
Rotación de cuerpo rígido
La rotación de un cuerpo rígido es un movimiento que ocurre cuando un cuerpo sólido se mueve en una trayectoria circular alrededor de algo. El movimiento de rotación se puede dividir en dos tipos de rotación: rotación sobre un eje fijo y rotación sobre un punto fijo. Se dice que la rotación alrededor de un eje fijo es cuando el cuerpo gira alrededor de un eje que tiene una ubicación y orientación fijas en relación con el cuerpo. El ejemplo de tales rotaciones incluye: puerta con bisagras. El segundo tipo de movimiento de rotación implica la rotación del cuerpo alrededor de un punto. El trompo de un niño es un ejemplo de este tipo de movimiento de rotación.
Velocidad angular
La velocidad angular se define como el desplazamiento angular con respecto al tiempo. Por ejemplo, una motocicleta dando vueltas sobre una pista circular en el pozo de la muerte, un tiovivo, etc. Para un cuerpo que gira alrededor de un eje fijo, el ángulo que cubre el cuerpo cambia con el tiempo. Denotemos el ángulo que abarca el cual es
![]()
En los casos en que el movimiento de rotación no es constante, se calcula la velocidad angular instantánea.
Momento angular
Se requiere fuerza para poner el cuerpo en movimiento de traslación. Hay paralelismos entre la rotación y el movimiento de traslación. Muchas cantidades, como el desplazamiento, la aceleración, la velocidad, etc., tienen valores correspondientes en el dominio rotacional. El par es análogo a la fuerza en el movimiento de rotación. Torque trae un cambio en el momento angular del sistema. El momento angular es análogo al momento lineal en el caso del movimiento de traslación. En la figura se da una partícula cuyo vector de posición con respecto al origen O es “r”. «p» denota el momento lineal de la partícula que se mueve alrededor de ese punto. En ese caso, el momento angular está dado por,
l = r × pag
Este es el producto cruzado del vector de posición y el vector de momento lineal. La magnitud del vector está dada por,
l = rpsin(θ)
La relación entre el par y la fuerza también se puede derivar de estas ecuaciones. Derivando la ecuación anterior,
l = r × pag
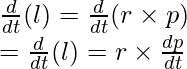
En el caso del momento angular de un sistema de partículas, el momento angular del sistema viene dado por la suma vectorial del momento individual de las partículas.
L = l 1 + l 2 + l 3 + .. l norte
L = r 1 × pag 1 + r 2 × pag 2 + r 3 × pag 3 …. r norte × pag norte
Esfuerzo de torsión
El par es análogo a la fuerza en el caso del movimiento de rotación. Esto también se llama el momento de la fuerza. Esto provoca una aceleración angular en el cuerpo, lo que significa obligar a cambiar el estado de rotación del cuerpo. Imagine abrir o cerrar la puerta de una habitación, en este caso, el movimiento de la puerta es un movimiento circular y, por lo tanto, se aplica un par de torsión a la puerta. En resumen, la fuerza aplicada para mover un cuerpo en movimiento circular es el par. Sea una partícula P situada lejos del origen en un punto cuyo vector de posición está dado por, Si la fuerza F actúa sobre la partícula, el momento de la fuerza está dado por,
![]()
Es una cantidad vectorial. La magnitud del torque está dada por,
Aquí, “r” es la magnitud del vector de posición y θ es el ángulo entre el vector de posición y la fuerza. En la fórmula, la parte «rsin» es la distancia perpendicular de la fuerza desde el eje del cuerpo rígido.
Las dimensiones del par están dadas por ML 2 T -2 . Estas también son dimensiones de energía, pero estas cantidades no deben confundirse como similares. Son magnitudes muy diferentes. La unidad de par es N -m.
Problemas de muestra
Pregunta 1: El vector de posición y el momento lineal de un cuerpo vienen dados por r = i + j + km y p = i + j Kg/s. Encuentre el momento angular.
Responder:
El momento angular está dado por,
l = r × pag
Dado: r = i + j + k, p = i + j
Pregunta 2: Encuentra el momento angular del sistema de dos partículas que giran alrededor del origen a una distancia de 10m con un momento lineal de 100Kg/s y 20 Kg/s.
Responder:
El momento angular está dado por,
l = rpsin(θ)
Dado: r = 10 m, p 1 = 100 Kgm/s, p 2 = 20 Kgm/s y el ángulo es un ángulo recto.
Dado que el sistema consta de dos partículas. El momento angular total será la suma del momento angular de estas partículas.
l = rp 1 + rp 2
l = (10)(100) + (10)(20)
l = 1000 + 200
l = 1200
Pregunta 3: Averigüe el par de torsión en la puerta si se aplica una fuerza de 10 N en la puerta a 0,5 m de la bisagra.
Responder:
El par está dado por,
τ = F × r
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación.
Dado: r = 0.5m y F = 10N.
Reemplazando los valores en la ecuación,
τ = F × r
⇒ τ = 10 × 0,5
⇒ τ = 5 Nm
Pregunta 4: Averigüe el par de torsión en la puerta si se aplica una fuerza de 100 N en la puerta a 0,5 m de la bisagra.
Responder:
El par está dado por,
τ = F × r
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación.
Dado: r = 0.5m y F = 100N.
Reemplazando los valores en la ecuación,
τ = F × r
⇒ τ = 100 × 0,5
⇒ τ = 50 Nm
Pregunta 5: Un objeto que realiza un movimiento circular alcanza una velocidad de 40 rad/s en 4 segundos. Encuentre el desplazamiento angular del objeto en el proceso.
Responder:
Sea ω 0 la velocidad angular inicial y ω la velocidad angular final.
Dado: ω 0 = 0 , ω = 40 y t = 4.
Para averiguar el valor de «a», se puede utilizar la primera ecuación de movimiento.
ω= ω 0 +αt
Reemplazando los valores en esta ecuación,
40 = 0 + α(4)
⇒ α = 10
Para averiguar la distancia, se utilizará una tercera ecuación de movimiento.
ω 2 = ω 0 2 +2α()
⇒ 40 2 = 0 + 2(10)()
⇒ 16000 = 20()
⇒ 80 =()
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA