Derivado total – Barcelona Geeks

La derivada total de una función f en un punto es una aproximación cerca del punto de la función wrt (con respecto a) sus argumentos (variables). La derivada total nunca aproxima la función con una sola variable si dos o más variables están presentes en la función. A veces, la derivada total es lo mismo que la derivada parcial o la derivada ordinaria de la función.

Para la función compuesta:

En general compuesta, la función no es más que una función de dos o más variables dependientes que dependen de cualquier variable común t. Los valores de la función compuesta se obtienen de ambas variables.

Si u= f(x,y) , donde x e y son variables dependientes en t, entonces también podemos expresar u como una función de t. Sustituyendo el valor de x, y en f(x,y) . Así, encontramos la derivada ordinaria que se llama la derivada total de u .

Ahora, para encontrar $\frac{du}{dt}$ sin sustituir realmente el valor de xey en f(x,y).

$\frac{du}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

De manera similar, si u = f(x,y,z) donde x, y, z son todas funciones de una variable t , entonces la regla de la string es:

$\frac{du}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t} + \frac{\partial u }{\partial z}. \frac{\partial z }{\partial t}$

Pregunta: Dado, $u = sin\frac{x}{y} , x = e^{t}, y= t^{2}, find \frac{du}{dt}$ en función de t . Verifique su resultado por sustitución directa.

Solución: Tenemos, $\frac{du}{dt} = \frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

= $cos\frac{x}{y} . \frac{1}{y} . _e{t} + (cos\frac{x}{y}) (\frac{-x}{_y{2}^{ }}) .2t$

poner valores de x e y en las ecuaciones anteriores

= $cos\frac{_e{t}}{_t{2}} . \frac{_e{t}}{_t{2}} -2cos\frac{_e{t}}{_t{2}} . _e{t}._t{3}$

$\frac{du}{dt} = (t-\frac{2}{_t{3}})._e{t}.cos\frac{_e{t}}{_t{2}}$

Pregunta: Dado, f(x,y) =e ^x seny , x=t ³ +1 y y=t ⁴ +1. Entonces df/dt en t =1.

Solución: Sea f(x,y) =e ^x sen

$\frac{df}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

= e ^x siny.(3t ² ) + acogedor .e ^x .(4t ³ )

Como sabemos, x= t ³ +1 y y= t ⁴ +1

valores de x e y en t =1, x=2 e y=2

$\frac{df}{dt} = (e^{2})(sin2)(12) + (cos2)(e^{2})(32)$

=(2,718) ² (0,0349)(12) +(0,9994)(2,718) ² (32)

= 238,97

Para función implícita:

La función implícita es una función cuyas variables no son variables completamente independientes. Sea una función f(x,y) donde x es variable independiente pero y es x variable dependiente.

Si f(x, y)= c (constante) es una función implícita y existe una relación entre xey que se define como una función diferenciable de x .

Aquí, f(x,y) = constante

Para la función implícita, consideremos x una variable independiente e y es una función de x .

f(x,y) = c ……..eq (1)

por definición de coeficiente diferencial total.

Pregunta: Si u = xlogxy donde x ³ +y ³ +3xy=1 , encuentre du/dx.

Solución: Tenemos x ³ +y ³ +3xy=1 ……….(1)

$\frac{du}{dx}=\frac{\partial u}{\partial x}.\frac{dy}{dx} +\frac{\partial u}{\partial y}.\frac{dy}{dx}$

= $(logxy +1) + \frac{x}{y}.\frac{dy}{dx} ..........(2)$

de la ecuación……….(1)

$\frac {dy}{dx} = -\frac{\frac{∂f}{∂x}} { \frac{∂f}{∂y}}$

$\frac{dy}{dx} = -\frac {(3x^{2} + 3y)}{(3y^{2} + 3x)}$

$= -\frac{(x^{2} +y)}{(y^{2} +x)}t$

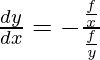
después de poner valor en la ecuación (2)

$\frac{du}{dx} = (logxy +1) - (\frac{x}{y})\frac {(x^{2}+y)}{(y^{2}+x)} .$

Publicación traducida automáticamente

Artículo escrito por uditsharma333jj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Para la función compuesta:

Para función implícita:

Deja una respuesta Cancelar la respuesta