Desbordamiento en la suma aritmética en el sistema numérico binario – Part 1

En la arquitectura de computadoras, el Sistema Numérico Complementario a 2 es ampliamente utilizado. La discusión sobre el desbordamiento aquí se centrará principalmente en el Sistema de cortesía de 2. 

N-bit El sistema de números complementarios a 2 puede representar números de  hasta 
4 Bits puede representar números de (-8 a 7) 
5 bits pueden representar números de (-16 a 15) en el sistema complementario de 2. 

Desbordamiento Ocurre con respecto a la suma cuando se suman 2 Números Complementarios a 2 de N bits y la respuesta es demasiado grande para caber en ese Grupo de N bits. 

Una computadora tiene registros fijos de N bits. La adición de dos números de N bits dará como resultado un número máximo de N+1 bits. Ese bit adicional se almacena en la bandera de acarreo. Pero Carry no siempre indica desbordamiento. 

Sumar 7 + 1 en 4 bits debe ser igual a 8. Pero 8 no se puede representar con el número de complemento de 2 de 4 bits porque está fuera de rango. Se sumaron dos números positivos y la respuesta que obtuvimos es negativa (-8). Aquí Carry también es 0. Normalmente se deja que el programador detecte el desbordamiento y se ocupe de esta situación. 

Detección de desbordamiento: 
el desbordamiento se produce cuando:  

1. Se suman dos números negativos y la respuesta es positiva o 
2. Se suman dos números positivos y la respuesta es negativa. 

Por lo tanto, el desbordamiento se puede detectar al verificar el bit más significativo (MSB) de dos operandos y responder. Pero en lugar de usar el desbordamiento del comparador de 3 bits, también se puede detectar usando el comparador de 2 bits simplemente marcando Carry-in (C-in) y Carry-Out (C-out) de MSB. Considere la adición de N bits del número de complemento a 2. 

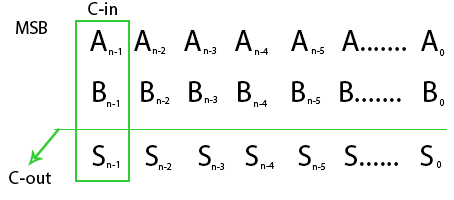
Desbordamiento Ocurre cuando C-in  C-out. La expresión anterior para el desbordamiento se puede explicar a partir del análisis a continuación.  

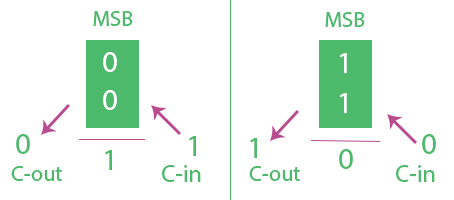
En la primera figura, el MSB de dos números es 0, lo que significa que son positivos. Aquí, si C-in es 1 , obtenemos MSB de respuesta como 1 significa que la respuesta es negativa (desbordamiento) y C-out como 0. C-in  C-out, por lo tanto, desbordamiento. 

En la segunda figura, el MSB de dos números es 1, lo que significa que son negativos. Aquí, si C-in es 0 , obtenemos la respuesta MSB como 0 significa que la respuesta es positiva (desbordamiento) y C-out como 1. C-in  C-out, por lo tanto, desbordamiento. 
Los lectores también pueden probar otras combinaciones de c-in c-out y MSB para verificar el desbordamiento. 

Por lo tanto, Carry-in y Carry-out en MSB son suficientes para detectar el desbordamiento. 

Por encima de XOR Gate se puede utilizar para detectar desbordamiento.