Descomposición ligera pesada | Serie 1 (Introducción)

La descomposición Heavy Light (HLD) es una de las técnicas más utilizadas en la programación competitiva .

Problema de ejemplo: comprendamos la descomposición pesada-ligera (HLD) con la ayuda del siguiente ejemplo.

Supongamos que tenemos un árbol desequilibrado (no necesariamente un árbol binario) de n Nodes , y tenemos que realizar operaciones en el árbol para responder a una serie de consultas, cada una puede ser de uno de los dos tipos:

1. change(a, b) : Actualiza el peso del a ^-ésimo borde a b.
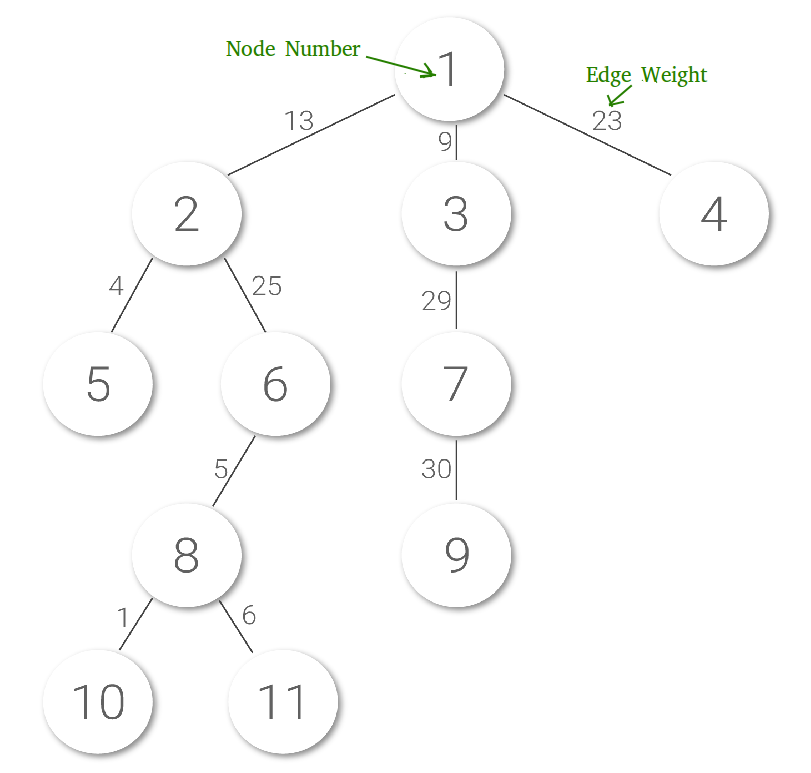
2. maxEdge(a, b) : Imprime el peso máximo del borde en la ruta desde el Node a hasta el Node b. Por ejemplo maxEdge(5, 10) debe imprimir 25.

Suponga que los Nodes están numerados del 1 al n. Debe haber n-1 aristas . Los pesos de los bordes son números naturales. Suponga también que ambos tipos de consultas están intercaladas (aproximadamente iguales en número) y, por lo tanto, ningún tipo puede dejarse de lado para comprometer la complejidad.

Solución simple: una solución simple es recorrer el árbol completo para cualquier consulta. La complejidad temporal de cada consulta en esta solución es O(n).

Solución basada en HLD:
Tras una cuidadosa observación de las dos operaciones, nos damos cuenta de que las hemos visto en alguna parte. ¡Eureka!
Árboles de segmentos
. A
Árbol de segmentos
se puede utilizar para realizar ambos tipos en O(log(n)). ¡Pero espera! A
Árbol de segmentos
se puede construir a partir de un array/string unidimensional (conjunto de Nodes enlazados uno tras otro), y lo que tenemos aquí es un árbol. Entonces, ¿podemos reducir el árbol a strings?

La solución basada en HLD discutida en la publicación toma O(log ² (n)) para maxEdge() y O(log n) para change().

El tamaño de un Node x es el número de Nodes en el subárbol enraizados con el Node x. Aquí hay una imagen que muestra los tamaños de los subárboles de cada Node escrito encima de ellos: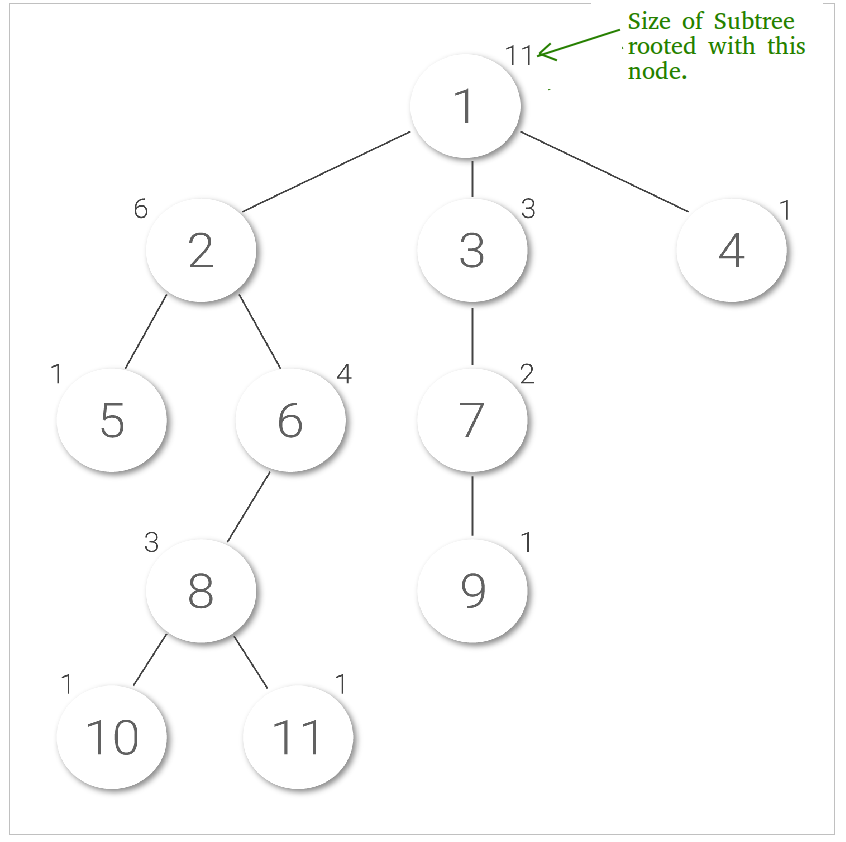

El HLD de un árbol enraizado es un método para descomponer los vértices del árbol en strings separadas (no hay dos strings que compartan un Node), para lograr límites de tiempo asintóticos importantes para ciertos problemas que involucran árboles.

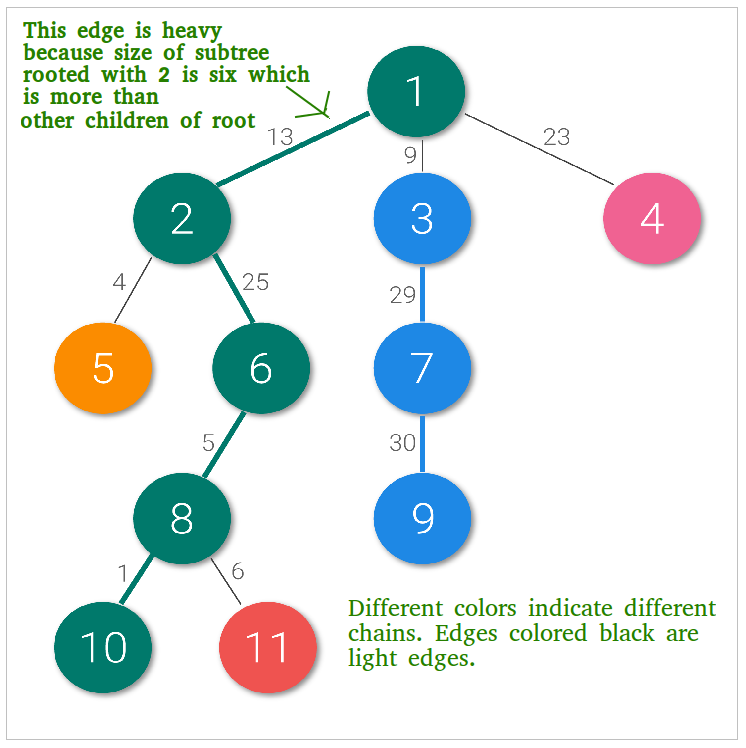
HLD también se puede ver como ‘colorear ‘ los bordes del árbol. El ‘Heavy-Light’ proviene de la forma en que segregamos los bordes. Usamos el tamaño de los subárboles enraizados en los Nodes como nuestro criterio.

Una arista es pesada si tamaño(v) > tamaño(u) donde u es cualquier hermano de v. Si resultan ser iguales, elegimos una v como especial.

Operación de cambio (u, v):
dado que el árbol de segmentos se usa como estructura de datos subyacente para representar strings individuales, el cambio se realiza mediante la actualización del árbol de segmentos . Entonces, la complejidad de tiempo de la operación de cambio es O (Log n).

operación maxEdge(u, v):

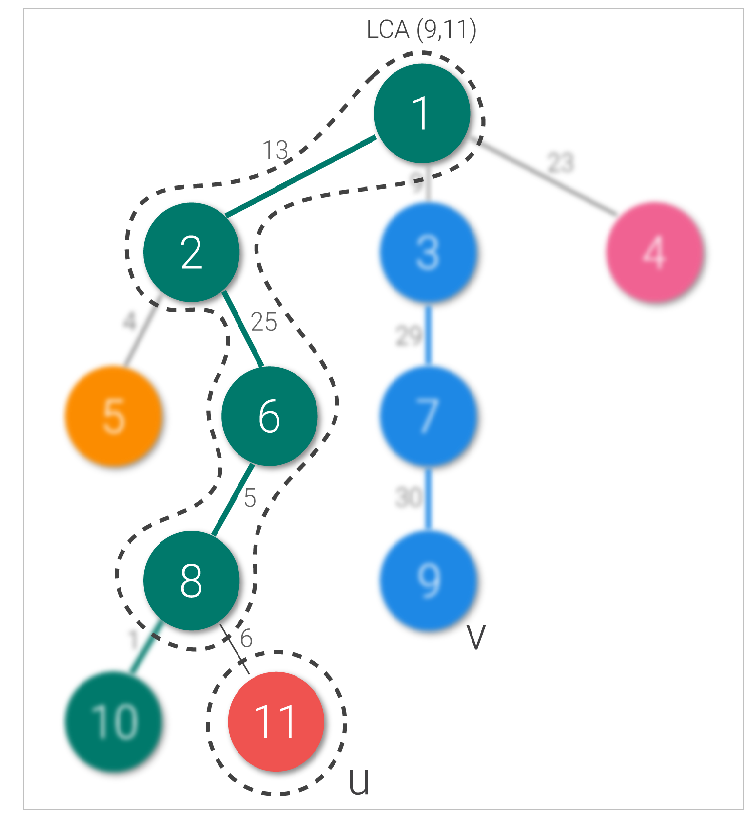
1. Primero encontramos LCA de dos Nodes. Digamos que el Node u es 11 y el Node v es 9. Su LCA es el Node 1.
2. Luego trepamos por el árbol desde el Node u hasta el lca. Si los Nodes u y lca pertenecen a la misma string, encontramos el máximo del rango que representa los bordes entre ellos utilizando el árbol de segmentos. De lo contrario, encontramos el máximo de la string a la que pertenece u, luego cambiamos de string y repetimos mientras no estemos en la misma string.
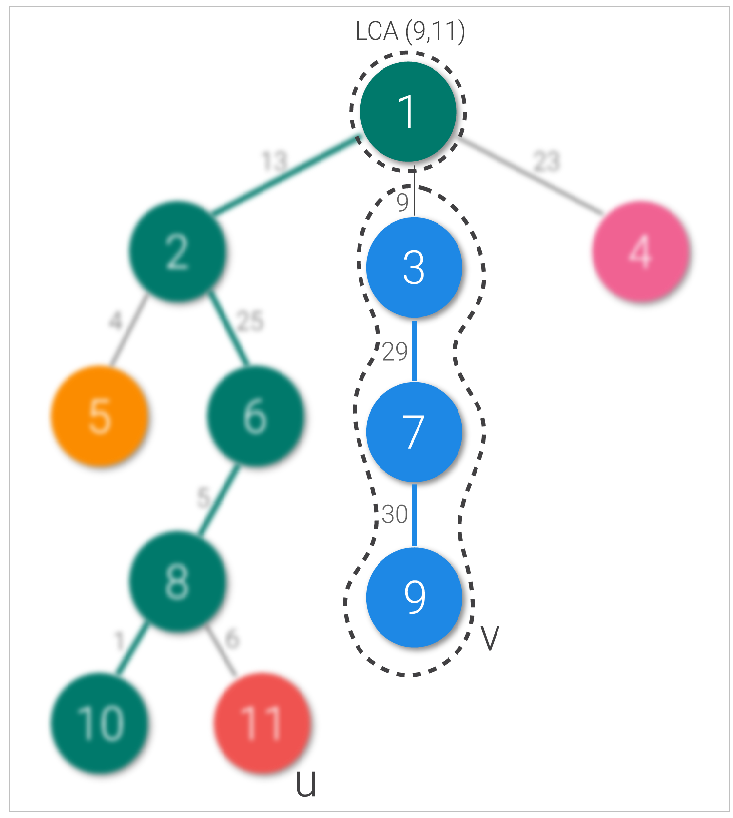
3. Repetimos el mismo paso (como el paso 2) de v a lca y devolvemos un máximo de dos pesos.

Según nuestro ejemplo anterior, tomemos u como el Node 11 yv como el Node 9. LCA es el Node 1. Pasamos del Node 11 al Node 1 y cambiamos las strings una vez. Cuando cambiamos de string, cambiamos de nuestro Node consultado al padre o cabeza de la string a la que pertenece (11 cambia a 8 aquí). De manera similar, se consultó el Node 9 al Node 3 (incluido el borde claro) y la string cambió (el Node cambió a 1).

La complejidad temporal de maxEdge es O (log ² (n)). Consultar el máximo de una string lleva un tiempo O(log(n)) ya que las strings se representan mediante el árbol de segmentos y hay como máximo strings O(log(n)).

¿Cómo es el número de strings O(log(n))?
Todas las strings están conectadas por un borde ligero (ver ejemplos anteriores). Entonces, el número de strings está limitado por el número de aristas claras en cualquier camino. Si seguimos un borde claro desde la raíz, el subárbol enraizado en el vértice resultante tiene como máximo un tamaño de n/2. Si repetimos, aterrizamos en un vértice con tamaño de subárbol como máximo n/4, y así sucesivamente. Concluimos que

La idea principal de Heavy Light Decomposition de un árbol desequilibrado es unir los vértices de caminos largos (o pesados) en strings para que estas strings lineales puedan consultarse en tiempo O (Log n) utilizando una estructura de datos como Segment Tree.

En el siguiente artículo , se analiza como ejemplo la representación en árbol de segmentos de las strings con más detalle y la implementación de la solución HLD para el problema.

Descomposición ligera pesada | Conjunto 2 (Implementación)

Este artículo es una contribución de Yash Varyani . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.