Requisito previo: Introducción y DFS
La tarea es encontrar LCA de dos Nodes dados en un árbol (no necesariamente un árbol binario). En publicaciones anteriores, hemos visto cómo calcular LCA utilizando el enfoque Sparse Matrix DP . En esta publicación, veremos una optimización realizada en el método Naive mediante la técnica de descomposición sqrt que funciona bien sobre el enfoque Naive.
Enfoque ingenuo
Para calcular el LCA de dos Nodes primero, traeremos ambos Nodes a la misma altura haciendo que el Node con mayor profundidad salte un padre hacia arriba en el árbol hasta que ambos Nodes estén a la misma altura. Una vez que ambos Nodes estén a la misma altura, podemos comenzar a saltar uno de los padres para ambos Nodes simultáneamente hasta que ambos Nodes se vuelvan iguales y ese Node será el LCA de los dos Nodes originalmente dados.
Considere el siguiente árbol n-ario con profundidad 9 y examinemos cómo funciona el enfoque ingenuo para este árbol de muestra.
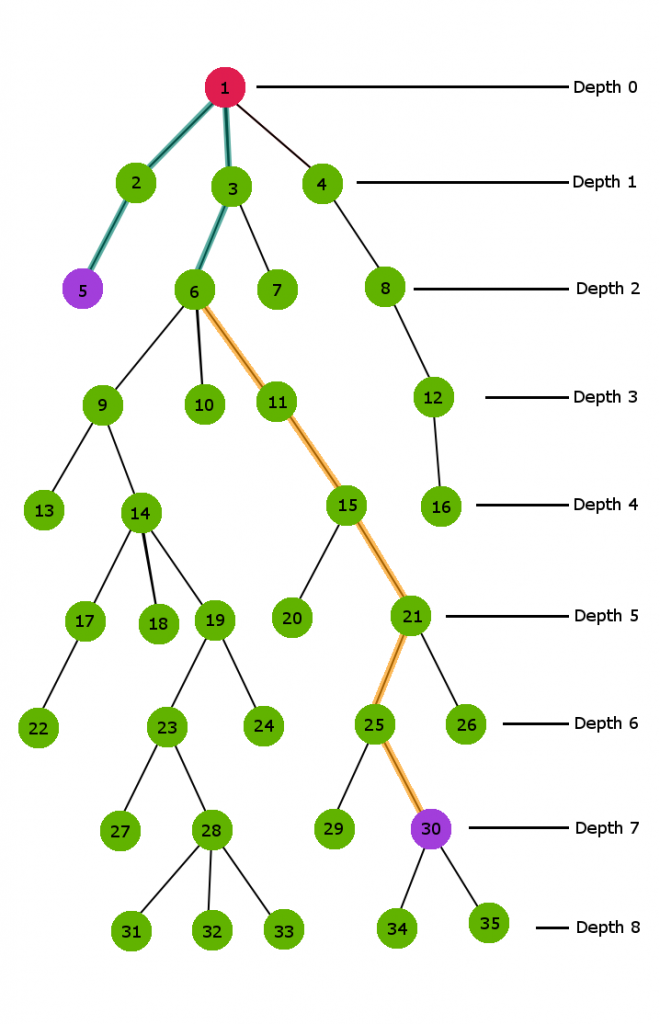
Aquí, en el árbol anterior, necesitamos calcular el LCA del Node 6 y el Node 30.
Claramente, el Node 30 tiene mayor profundidad que el Node 6. Entonces, antes que nada, comenzamos a saltar un padre arriba para el Node 30 hasta alcanzar el valor de profundidad del Node 6. es decir, en la profundidad 2.
La ruta de color naranja en la figura anterior demuestra la secuencia de salto para alcanzar la profundidad 2. En este procedimiento, simplemente saltamos un padre por encima del Node actual.
Ahora ambos Nodes están a la misma profundidad 2. Por lo tanto, ahora ambos Nodes saltarán a uno de los padres hasta que ambos Nodes se vuelvan iguales. Este Node final en el que ambos Nodes se vuelven iguales por primera vez es nuestro LCA.
La ruta de color azul en la figura anterior muestra la ruta de salto para ambos Nodes.
Implementación:
C++
// Naive C++ implementation to find LCA in a tree
#include<bits/stdc++.h>
using namespace std;
#define MAXN 1001
int depth[MAXN]; // stores depth for each node
int parent[MAXN]; // stores first parent for each node
vector < int > adj[MAXN];
void addEdge(int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void dfs(int cur, int prev)
{
// marking parent for each node
parent[cur] = prev;
// marking depth for each node
depth[cur] = depth[prev] + 1;
// propagating marking down the tree
for (int i=0; i<adj[cur].size(); i++)
if (adj[cur][i] != prev)
dfs(adj[cur][i],cur);
}
void preprocess()
{
// a dummy node
depth[0] = -1;
// precalculating 1)depth. 2)parent.
// for each node
dfs(1,0);
}
// Time Complexity : O(Height of tree)
// recursively jumps one node above
// till both the nodes become equal
int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
swap(u, v);
v = parent[v];
return LCANaive(u,v);
}
// Driver function to call the above functions
int main(int argc, char const *argv[])
{
// adding edges to the tree
addEdge(1,2);
addEdge(1,3);
addEdge(1,4);
addEdge(2,5);
addEdge(2,6);
addEdge(3,7);
addEdge(4,8);
addEdge(4,9);
addEdge(9,10);
addEdge(9,11);
addEdge(7,12);
addEdge(7,13);
preprocess();
cout << "LCA(11,8) : " << LCANaive(11,8) << endl;
cout << "LCA(3,13) : " << LCANaive(3,13) << endl;
return 0;
}
Java
// Naive Java implementation to find LCA in a tree.
import java.io.*;
import java.util.*;
class GFG
{
static int MAXN = 1001;
// stores depth for each node
static int[] depth = new int[MAXN];
// stores first parent for each node
static int[] parent = new int[MAXN];
@SuppressWarnings("unchecked")
static Vector<Integer>[] adj = new Vector[MAXN];
static
{
for (int i = 0; i < MAXN; i++)
adj[i] = new Vector<>();
}
static void addEdge(int u, int v)
{
adj[u].add(v);
adj[v].add(u);
}
static void dfs(int cur, int prev)
{
// marking parent for each node
parent[cur] = prev;
// marking depth for each node
depth[cur] = depth[prev] + 1;
// propagating marking down the tree
for (int i = 0; i < adj[cur].size(); i++)
if (adj[cur].elementAt(i) != prev)
dfs(adj[cur].elementAt(i), cur);
}
static void preprocess()
{
// a dummy node
depth[0] = -1;
// precalculating 1)depth. 2)parent.
// for each node
dfs(1, 0);
}
// Time Complexity : O(Height of tree)
// recursively jumps one node above
// till both the nodes become equal
static int LCANaive(int u, int v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
int temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
// Driver Code
public static void main(String[] args)
{
// adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
System.out.println("LCA(11,8) : " + LCANaive(11, 8));
System.out.println("LCA(3,13) : " + LCANaive(3, 13));
}
}
// This code is contributed by
// sanjeev2552
Python3
# Python3 implementation to
# find LCA in a tree
MAXN = 1001
# stores depth for each node
depth = [0 for i in range(MAXN)];
# stores first parent for each node
parent = [0 for i in range(MAXN)];
adj = [[] for i in range(MAXN)]
def addEdge(u, v):
adj[u].append(v);
adj[v].append(u);
def dfs(cur, prev):
# marking parent for
# each node
parent[cur] = prev;
# marking depth for
# each node
depth[cur] = depth[prev] + 1;
# propagating marking down
# the tree
for i in range(len(adj[cur])):
if (adj[cur][i] != prev):
dfs(adj[cur][i], cur);
def preprocess():
# a dummy node
depth[0] = -1;
# precalculating 1)depth.
# 2)parent. for each node
dfs(1, 0);
# Time Complexity : O(Height of tree)
# recursively jumps one node above
# till both the nodes become equal
def LCANaive(u, v):
if (u == v):
return u;
if (depth[u] > depth[v]):
u, v = v, u
v = parent[v];
return LCANaive(u, v);
# Driver code
if __name__ == "__main__":
# adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
print('LCA(11,8) : ' +
str(LCANaive(11, 8)))
print('LCA(3,13) : ' +
str(LCANaive(3, 13)))
# This code is contributed by RUtvik_56
C#
// Naive C# implementation to find
// LCA in a tree.
using System;
using System.Collections;
class GFG{
static int MAXN = 1001;
// Stores depth for each node
static int[] depth = new int[MAXN];
// Stores first parent for each node
static int[] parent = new int[MAXN];
static ArrayList[] adj = new ArrayList[MAXN];
static void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static void dfs(int cur, int prev)
{
// Marking parent for each node
parent[cur] = prev;
// Marking depth for each node
depth[cur] = depth[prev] + 1;
// Propagating marking down the tree
for(int i = 0; i < adj[cur].Count; i++)
if ((int)adj[cur][i] != prev)
dfs((int)adj[cur][i], cur);
}
static void preprocess()
{
// A dummy node
depth[0] = -1;
// Precalculating 1)depth. 2)parent.
// for each node
dfs(1, 0);
}
// Time Complexity : O(Height of tree)
// recursively jumps one node above
// till both the nodes become equal
static int LCANaive(int u, int v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
int temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
// Driver Code
public static void Main(string[] args)
{
for(int i = 0; i < MAXN; i++)
adj[i] = new ArrayList();
// Adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
Console.WriteLine("LCA(11, 8) : " +
LCANaive(11, 8));
Console.WriteLine("LCA(3, 13) : " +
LCANaive(3, 13));
}
}
// This code is contributed by pratham76
Javascript
<script>
// Naive Javascript implementation to find
// LCA in a tree.
var MAXN = 1001;
// Stores depth for each node
var depth = Array(MAXN);
// Stores first parent for each node
var parent = Array(MAXN);
var adj = Array.from(Array(MAXN), ()=>Array());
function addEdge(u, v)
{
adj[u].push(v);
adj[v].push(u);
}
function dfs(cur, prev)
{
// Marking parent for each node
parent[cur] = prev;
// Marking depth for each node
depth[cur] = depth[prev] + 1;
// Propagating marking down the tree
for(var i = 0; i < adj[cur].length; i++)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
function preprocess()
{
// A dummy node
depth[0] = -1;
// Precalculating 1)depth. 2)parent.
// for each node
dfs(1, 0);
}
// Time Complexity : O(Height of tree)
// recursively jumps one node above
// till both the nodes become equal
function LCANaive(u, v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
var temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
// Driver Code
for(var i = 0; i < MAXN; i++)
adj[i] = [];
// Adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
document.write("LCA(11, 8) : " +
LCANaive(11, 8)+"<br>");
document.write("LCA(3, 13) : " +
LCANaive(3, 13));
// This code is contributed by famously.
</script>
LCA(11,8) : 4 LCA(3,13) : 3
Complejidad de tiempo : calculamos previamente la profundidad para cada Node utilizando un recorrido DFS en O(n) . Ahora, en el peor de los casos, los dos Nodes serán los dos Nodes más inferiores del árbol en diferentes ramas secundarias del Node raíz. Por lo tanto, en este caso, la raíz será el LCA de ambos Nodes. Por lo tanto, ambos Nodes tendrán que saltar exactamente h altura arriba, donde h es la altura del árbol. Entonces, para responder a cada consulta de LCA, la complejidad del tiempo será O(h) .
El truco de la descomposición Sqrt:
Clasificamos los Nodes del árbol en diferentes grupos según su profundidad. Suponiendo que la profundidad del árbol h es un cuadrado perfecto. Entonces, una vez más, como el enfoque general de descomposición sqrt , tendremos bloques o grupos sqrt (h). Los Nodes desde la profundidad 0 hasta la profundidad sqrt(h) – 1 se encuentran en el primer grupo; luego los Nodes que tienen profundidad sqrt(H) a 2*sqrt(h)-1 se encuentran en el segundo grupo y así sucesivamente hasta el último Node.
Realizamos un seguimiento del número de grupo correspondiente para cada Node y también la profundidad de cada Node. Esto se puede hacer con un solo dfs en el árbol (consulte el código para una mejor comprensión).
Truco Sqrt : –
En el enfoque ingenuo, estábamos saltando a un padre en el árbol hasta que ambos Nodes no estaban en la misma profundidad. Pero aquí realizamos el salto grupal. Para realizar este salto grupal, necesitamos dos parámetros asociados con cada Node: 1) padre y 2) padre de salto.
Aquí , el padre de cada Node se define como el primer Node sobre el Node actual que está directamente conectado a él, mientras que jump_parent para cada Node es el Node que es el primer ancestro del Node actual en el grupo justo encima del Node actual.
Entonces, ahora necesitamos mantener 3 parámetros para cada Node:
- profundidad
- padre
- salto_padre
Todos estos tres parámetros se pueden mantener en un dfs (consulte el código para una mejor comprensión)
Pseudocódigo para el proceso de optimización
LCAsqrt(u, v){
// assuming v is at greater depth
while (jump_parent[u]!=jump_parent[v]){
v = jump_parent[v];
}
// now both nodes are in same group
// and have same jump_parent
return LCAnaive(u,v);
}
El concepto clave aquí es que primero traemos ambos Nodes en el mismo grupo y tienen el mismo jump_parent escalando bloques descompuestos sobre el árbol uno por uno y luego, cuando ambos Nodes están en el mismo grupo y tienen el mismo jump_parent, usamos nuestro enfoque ingenuo para encontrar LCA de los Nodes.
Esta técnica de salto de grupo optimizada reduce el espacio de iteración por un factor de sqrt (h) y, por lo tanto, reduce la complejidad del tiempo (consulte a continuación para obtener un mejor análisis de la complejidad del tiempo)
Descompongamos el árbol anterior en grupos sqrt(h) (h = 9) y calculemos LCA para los Nodes 6 y 30.
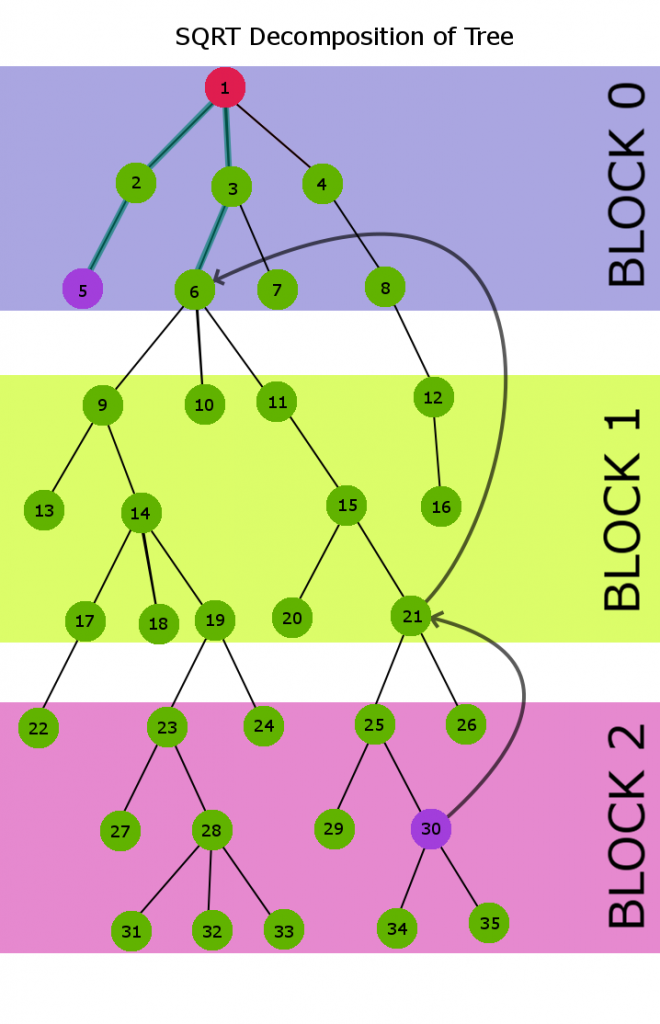
En el árbol descompuesto de arriba
Jump_parent[6] = 0 parent[6] = 3 Jump_parent[5] = 0 parent[5] = 2 Jump_parent[1] = 0 parent[1] = 0 Jump_parent[11] = 6 parent[11] = 6 Jump_parent[15] = 6 parent[15] = 11 Jump_parent[21] = 6 parent[21] = 15 Jump_parent[25] = 21 parent[25] = 21 Jump_parent[26] = 21 parent[26] = 21 Jump_parent[30] = 21 parent[30] = 25
Ahora, en esta etapa, Jump_parent para el Node 30 es 21 y Jump_parent para el Node 5 es 0, por lo tanto, subiremos a jump_parent [30], es decir, al Node 21.
Ahora, una vez más, Jump_parent del Node 21 no es igual a Jump_parent del Node 5, así que una vez más subiremos a jump_parent[21], es decir, al Node 6
En esta etapa jump_parent[6] == jump_parent[5], así que ahora usaremos nuestro enfoque de escalada ingenuo y subiremos un padre arriba para ambos Nodes hasta que llegue al Node 1 y eso será el LCA requerido.
La ruta azul en la figura anterior describe la secuencia de ruta de salto para el Node 6 y el Node 5.
Implementación:
C++
// C++ program to find LCA using Sqrt decomposition
#include "iostream"
#include "vector"
#include "math.h"
using namespace std;
#define MAXN 1001
int block_sz; // block size = sqrt(height)
int depth[MAXN]; // stores depth for each node
int parent[MAXN]; // stores first parent for
// each node
int jump_parent[MAXN]; // stores first ancestor in
// previous block
vector < int > adj[MAXN];
void addEdge(int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
swap(u,v);
v = parent[v];
return LCANaive(u,v);
}
// precalculating the required parameters
// associated with every node
void dfs(int cur, int prev)
{
// marking depth of cur node
depth[cur] = depth[prev] + 1;
// marking parent of cur node
parent[cur] = prev;
// making jump_parent of cur node
if (depth[cur] % block_sz == 0)
/* if it is first node of the block
then its jump_parent is its cur parent */
jump_parent[cur] = parent[cur];
else
/* if it is not the first node of this block
then its jump_parent is jump_parent of
its parent */
jump_parent[cur] = jump_parent[prev];
// propagating the marking down the subtree
for (int i = 0; i<adj[cur].size(); ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
// using sqrt decomposition trick
int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
// maintaining depth[v] > depth[u]
swap(u,v);
// climb to its jump parent
v = jump_parent[v];
}
// u and v have same jump_parent
return LCANaive(u,v);
}
void preprocess(int height)
{
block_sz = sqrt(height);
depth[0] = -1;
// precalculating 1)depth. 2)parent. 3)jump_parent
// for each node
dfs(1, 0);
}
// Driver function to call the above functions
int main(int argc, char const *argv[])
{
// adding edges to the tree
addEdge(1,2);
addEdge(1,3);
addEdge(1,4);
addEdge(2,5);
addEdge(2,6);
addEdge(3,7);
addEdge(4,8);
addEdge(4,9);
addEdge(9,10);
addEdge(9,11);
addEdge(7,12);
addEdge(7,13);
// here we are directly taking height = 4
// according to the given tree but we can
// pre-calculate height = max depth
// in one more dfs
int height = 4;
preprocess(height);
cout << "LCA(11,8) : " << LCASQRT(11,8) << endl;
cout << "LCA(3,13) : " << LCASQRT(3,13) << endl;
return 0;
}
Java
// Java program to find LCA using Sqrt decomposition
import java.util.*;
class GFG
{
static final int MAXN = 1001;
static int block_sz; // block size = Math.sqrt(height)
static int []depth = new int[MAXN]; // stores depth for each node
static int []parent = new int[MAXN]; // stores first parent for
// each node
static int []jump_parent = new int[MAXN]; // stores first ancestor in
// previous block
static Vector <Integer > []adj = new Vector[MAXN];
static void addEdge(int u,int v)
{
adj[u].add(v);
adj[v].add(u);
}
static int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
// precalculating the required parameters
// associated with every node
static void dfs(int cur, int prev)
{
// marking depth of cur node
depth[cur] = depth[prev] + 1;
// marking parent of cur node
parent[cur] = prev;
// making jump_parent of cur node
if (depth[cur] % block_sz == 0)
/* if it is first node of the block
then its jump_parent is its cur parent */
jump_parent[cur] = parent[cur];
else
/* if it is not the first node of this block
then its jump_parent is jump_parent of
its parent */
jump_parent[cur] = jump_parent[prev];
// propagating the marking down the subtree
for (int i = 0; i < adj[cur].size(); ++i)
if (adj[cur].get(i) != prev)
dfs(adj[cur].get(i), cur);
}
// using sqrt decomposition trick
static int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
// maintaining depth[v] > depth[u]
int t = u;
u = v;
v = t;
}
// climb to its jump parent
v = jump_parent[v];
}
// u and v have same jump_parent
return LCANaive(u, v);
}
static void preprocess(int height)
{
block_sz = (int)Math.sqrt(height);
depth[0] = -1;
// precalculating 1)depth. 2)parent. 3)jump_parent
// for each node
dfs(1, 0);
}
// Driver code
public static void main(String []args)
{
for (int i = 0; i < adj.length; i++)
adj[i] = new Vector<Integer>();
// adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
// here we are directly taking height = 4
// according to the given tree but we can
// pre-calculate height = max depth
// in one more dfs
int height = 4;
preprocess(height);
System.out.print("LCA(11,8) : " + LCASQRT(11, 8) +"\n");
System.out.print("LCA(3,13) : " + LCASQRT(3, 13) +"\n");
}
}
// This code is contributed by aashish1995.
C#
// C# program to find LCA using Sqrt decomposition
using System;
using System.Collections.Generic;
public class GFG
{
static readonly int MAXN = 1001;
static int block_sz; // block size = Math.Sqrt(height)
static int []depth = new int[MAXN]; // stores depth for each node
static int []parent = new int[MAXN]; // stores first parent for
// each node
static int []jump_parent = new int[MAXN]; // stores first ancestor in
// previous block
static List <int > []adj = new List<int>[MAXN];
static void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static int LCANaive(int u, int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
// precalculating the required parameters
// associated with every node
static void dfs(int cur, int prev)
{
// marking depth of cur node
depth[cur] = depth[prev] + 1;
// marking parent of cur node
parent[cur] = prev;
// making jump_parent of cur node
if (depth[cur] % block_sz == 0)
/* if it is first node of the block
then its jump_parent is its cur parent */
jump_parent[cur] = parent[cur];
else
/* if it is not the first node of this block
then its jump_parent is jump_parent of
its parent */
jump_parent[cur] = jump_parent[prev];
// propagating the marking down the subtree
for (int i = 0; i < adj[cur].Count; ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
// using sqrt decomposition trick
static int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
// maintaining depth[v] > depth[u]
int t = u;
u = v;
v = t;
}
// climb to its jump parent
v = jump_parent[v];
}
// u and v have same jump_parent
return LCANaive(u, v);
}
static void preprocess(int height)
{
block_sz = (int)Math.Sqrt(height);
depth[0] = -1;
// precalculating 1)depth. 2)parent. 3)jump_parent
// for each node
dfs(1, 0);
}
// Driver code
public static void Main(String []args)
{
for (int i = 0; i < adj.Length; i++)
adj[i] = new List<int>();
// adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
// here we are directly taking height = 4
// according to the given tree but we can
// pre-calculate height = max depth
// in one more dfs
int height = 4;
preprocess(height);
Console.Write("LCA(11,8) : " + LCASQRT(11, 8) +"\n");
Console.Write("LCA(3,13) : " + LCASQRT(3, 13) +"\n");
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// Javascript program to find LCA
// using Sqrt decomposition
let MAXN = 1001;
// Block size = Math.sqrt(height)
let block_sz;
// Stores depth for each node
let depth = new Array(MAXN);
// Stores first parent for
// each node
let parent = new Array(MAXN);
// Stores first ancestor in
// previous block
let jump_parent = new Array(MAXN);
let adj = new Array(MAXN);
function addEdge(u, v)
{
adj[u].push(v);
adj[v].push(u);
}
function LCANaive(u, v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
let t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
// Precalculating the required parameters
// associated with every node
function dfs(cur, prev)
{
// Marking depth of cur node
depth[cur] = depth[prev] + 1;
// Marking parent of cur node
parent[cur] = prev;
// Making jump_parent of cur node
if (depth[cur] % block_sz == 0)
// If it is first node of the block
// then its jump_parent is its cur parent
jump_parent[cur] = parent[cur];
else
// If it is not the first node of this block
// then its jump_parent is jump_parent of
// its parent
jump_parent[cur] = jump_parent[prev];
// Propagating the marking down the subtree
for(let i = 0; i < adj[cur].length; ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
// Using sqrt decomposition trick
function LCASQRT(u, v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
// Maintaining depth[v] > depth[u]
let t = u;
u = v;
v = t;
}
// Climb to its jump parent
v = jump_parent[v];
}
// u and v have same jump_parent
return LCANaive(u, v);
}
function preprocess(height)
{
block_sz = parseInt(Math.sqrt(height), 10);
depth[0] = -1;
// Precalculating 1)depth. 2)parent. 3)
// jump_parent for each node
dfs(1, 0);
}
// Driver code
for(let i = 0; i < adj.length; i++)
adj[i] = [];
// Adding edges to the tree
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
// Here we are directly taking height = 4
// according to the given tree but we can
// pre-calculate height = max depth
// in one more dfs
let height = 4;
preprocess(height);
document.write("LCA(11,8) : " +
LCASQRT(11, 8) + "</br>");
document.write("LCA(3,13) : " +
LCASQRT(3, 13) + "</br>");
// This code is contributed by divyeshrabadiya07
</script>
LCA(11,8) : 4 LCA(3,13) : 3
Nota: el código anterior funciona incluso si la altura no es un cuadrado perfecto.
Ahora veamos cómo se cambia la Complejidad del tiempo con esta sencilla técnica de agrupación:
Análisis de Complejidad de Tiempo:
Hemos dividido el árbol en grupos sqrt(h) según su profundidad y cada grupo contiene Nodes que tienen una diferencia máxima en su profundidad igual a sqrt(h). Ahora, una vez más, tomemos un ejemplo del peor de los casos, digamos que el primer Node ‘u’ está en el primer grupo y el Node ‘v’ está en el grupo sqrt (h) th (último grupo). Entonces, primero haremos saltos grupales (saltos de un solo grupo) hasta llegar al grupo 1 del último grupo; Esto tomará exactamente sqrt(h) – 1 iteraciones o saltos. Entonces, hasta este paso, la complejidad del tiempo es O(sqrt(h)) .
Ahora, una vez que estamos en el mismo grupo, llamamos a la función LCAnaive. La complejidad de tiempo para LCA_Naive es O(sqrt(h’)), donde h’ es la altura del árbol. Ahora, en nuestro caso, el valor de h’ será sqrt(h), porque cada grupo tiene un subárbol con una altura máxima de sqrt(h). Entonces, la complejidad de este paso también es O(sqrt(h)).
Por lo tanto, la Complejidad de Tiempo total será O(sqrt(h) + sqrt(h)) ~ O(sqrt(h)) .
Este artículo es una contribución de Nitish Kumar . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA