Descripción general de las estructuras de datos | Conjunto 3 (Gráfico, Triángulo, Árbol de segmentos y Árbol de sufijos)

Hemos discutido a continuación las estructuras de datos en los dos conjuntos anteriores. Conjunto 1: descripción general de la array, la lista vinculada, la cola y la pila. Conjunto 2: descripción general del árbol binario, BST, montón y hash. 9. Gráfico 10. Trie 11. Árbol de segmentos 12. Árbol de sufijos

Gráfico: el gráfico es una estructura de datos que consta de los siguientes dos componentes:

1. Un conjunto finito de vértices también se llama Nodes.
2. Un conjunto finito de pares ordenados de la forma (u, v) se llama arista. El par está ordenado porque (u, v) no es lo mismo que (v, u) en el caso de un grafo dirigido (di-grafo). El par de formas (u, v) indica que hay una arista desde el vértice u hasta el vértice v. Las aristas pueden contener peso/valor/costo.

V -> Número de Vértices. E -> Número de Aristas. El gráfico se puede clasificar sobre la base de muchas cosas, a continuación se muestran las dos clasificaciones más comunes:

1. Dirección: Gráfico no dirigido: el gráfico en el que todos los bordes son bidireccionales. Gráfico dirigido: el gráfico en el que todos los bordes son unidireccionales.
2. Peso: Gráfico ponderado: el gráfico en el que el peso está asociado con los bordes. Gráfico no ponderado: el gráfico en el que no hay peso asociado con los bordes.

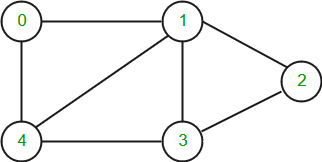
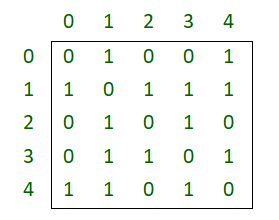
Los gráficos se pueden representar de muchas maneras, a continuación se muestran las dos representaciones más comunes: Tomemos el siguiente gráfico de ejemplo para ver dos representaciones del gráfico.

 

Time Complexities in case of Adjacency Matrix :
Traversal :(By BFS or DFS) O(V^2)
Space : O(V^2)

Time Complexities in case of Adjacency List :
Traversal :(By BFS or DFS) O(V + E)
Space : O(V+E)

Ejemplos: El ejemplo más común del gráfico es encontrar el camino más corto en cualquier red. Usado en google maps o bing. Otra aplicación de uso común de los gráficos son los sitios web de redes sociales donde la sugerencia de amistad depende de la cantidad de sugerencias intermedias y otras cosas.

prueba

Trie es una estructura de datos eficiente para buscar palabras en diccionarios, la complejidad de búsqueda con Trie es lineal en términos de longitud de palabra (o clave) a buscar. Si almacenamos claves en un árbol de búsqueda binaria, un BST bien equilibrado necesitará un tiempo proporcional a M * log N, donde M es la longitud máxima de la string y N es el número de claves en el árbol. Usando trie, podemos buscar la clave en tiempo O(M). Así que es mucho más rápido que BST. Hashing también proporciona búsqueda de palabras en tiempo O(n) en promedio. Pero las ventajas de Trie son que no hay colisiones (como hashing), por lo que la complejidad de tiempo en el peor de los casos es O (n). Además, lo más importante es la búsqueda de prefijos. Con Trie, podemos encontrar todas las palabras que comienzan con un prefijo (Esto no es posible con Hashing). El único problema con Tries es que requieren mucho espacio adicional. Los intentos también se conocen como árboles radix o árboles de prefijos.

The Trie structure can be defined as follows :
struct trie_node
{
    int value; /* Used to mark leaf nodes */
    trie_node_t *children[ALPHABET_SIZE];
};


                       root
                    /   \    \
                    t   a     b
                    |   |     |
                    h   n     y
                    |   |  \  |
                    e   s  y  e
                 /  |   |
                 i  r   w
                 |  |   |
                 r  e   e
                        |
                        r

The leaf nodes are in blue.

Insert time : O(M) where M is the length of the string.
Search time : O(M) where M is the length of the string.
Space : O(ALPHABET_SIZE * M * N) where N is number of 
        keys in trie, ALPHABET_SIZE is 26 if we are 
        only considering upper case Latin characters.
Deletion time: O(M)

Ejemplo: el uso más común de Tries es implementar diccionarios debido a la capacidad de búsqueda de prefijos. Los intentos también son adecuados para implementar algoritmos de coincidencia aproximada, incluidos los que se usan en la revisión ortográfica. También se utiliza para buscar contactos en la lista de contactos móviles O en el directorio telefónico.

Árbol de segmentos

Esta estructura de datos generalmente se implementa cuando hay muchas consultas sobre un conjunto de valores. Estas consultas involucran mínimo, máximo, suma, .. etc. en un rango de entrada de un conjunto dado. Las consultas también implican la actualización de valores en el conjunto dado. Los árboles de segmentos se implementan mediante una array.

Construction of segment tree : O(N)
Query : O(log N)
Update : O(log N)
Space : O(N) [Exact space = 2*N-1]

Ejemplo: Se usa cuando necesitamos encontrar el Máximo/Mínimo/Suma/Producto de números en un rango.

Árbol de sufijos

El árbol de sufijos se utiliza principalmente para buscar un patrón en un texto. La idea es preprocesar el texto para que la operación de búsqueda se pueda realizar en un tiempo lineal en términos de longitud del patrón. Los algoritmos de búsqueda de patrones como KMP, Z, etc. toman un tiempo proporcional a la longitud del texto. Esta es realmente una gran mejora porque la longitud del patrón es generalmente mucho más pequeña que la del texto. Imagine que hemos almacenado la obra completa de William Shakespeare y la hemos preprocesado. Puede buscar cualquier string en el trabajo completo en un tiempo justo proporcional a la longitud del patrón. Pero usar Suffix Tree puede no ser una buena idea cuando el texto cambia con frecuencia, como un editor de texto, etc. 1) Generar todos los sufijos del texto dado.

  

Ejemplo: se utiliza para buscar todas las apariciones del patrón en una string. También se utiliza para encontrar la substring repetida más larga (cuando el texto no cambia con frecuencia), la substring común más larga y el palíndromo más largo de una string. Este artículo es una contribución de Abhiraj Smit . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.