Nos dan un gráfico dirigido. Necesitamos calcular si el gráfico tiene un ciclo negativo o no. Un ciclo negativo es aquel en el que la suma total del ciclo es negativa.
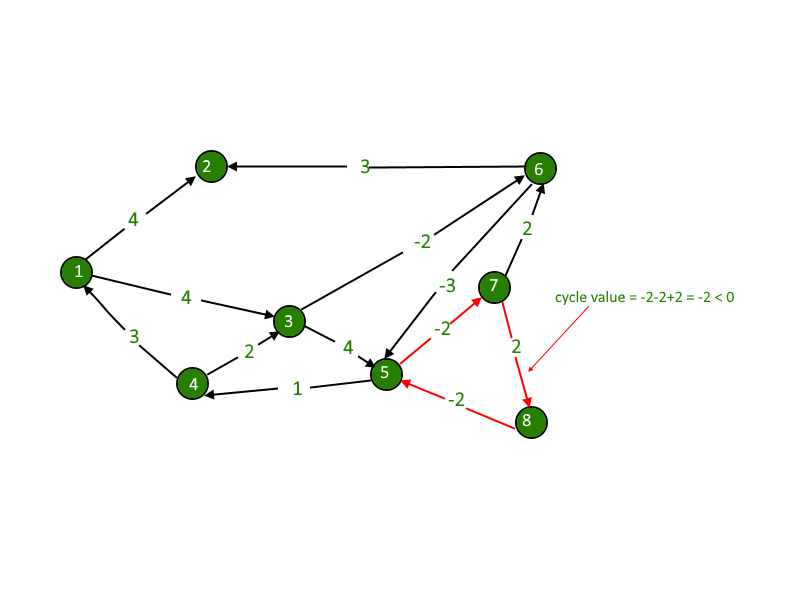
Los pesos negativos se encuentran en varias aplicaciones de gráficos. Por ejemplo, en lugar de pagar el costo de un camino, podemos obtener alguna ventaja si seguimos el camino.
Ejemplos:
Input : 4 4
0 1 1
1 2 -1
2 3 -1
3 0 -1
Output : Yes
The graph contains a negative cycle.
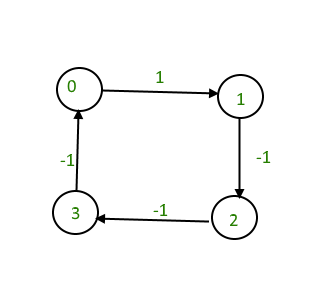
Hemos discutido la solución basada en el algoritmo Bellman Ford para este problema.
En esta publicación, se analiza la solución basada en el algoritmo Floyd Warshall que funciona tanto para gráficos conectados como desconectados.
La distancia de cualquier Node a sí mismo es siempre cero. Pero en algunos casos, como en este ejemplo, cuando recorremos más de 4 a 1, la distancia resulta ser -2, es decir, la distancia de 1 a 1 se convertirá en -2. Esta es nuestra trampa, solo tenemos que verificar la distancia de los Nodes de sí mismo y si resulta ser negativo, detectaremos el ciclo negativo requerido.
Implementación:
C++
// C++ Program to check if there is a negative weight
// cycle using Floyd Warshall Algorithm
#include<bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 4
/* Define Infinite as a large enough value. This
value will be used for vertices not connected
to each other */
#define INF 99999
// A function to print the solution matrix
void printSolution(int dist[][V]);
// Returns true if graph has negative weight cycle
// else false.
bool negCyclefloydWarshall(int graph[][V])
{
/* dist[][] will be the output matrix that will
finally have the shortest
distances between every pair of vertices */
int dist[V][V], i, j, k;
/* Initialize the solution matrix same as input
graph matrix. Or we can say the initial values
of shortest distances are based on shortest
paths considering no intermediate vertex. */
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
/* Add all vertices one by one to the set of
intermediate vertices.
---> Before start of a iteration, we have shortest
distances between all pairs of vertices such
that the shortest distances consider only the
vertices in set {0, 1, 2, .. k-1} as intermediate
vertices.
----> After the end of a iteration, vertex no. k is
added to the set of intermediate vertices and
the set becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++)
{
// Pick all vertices as source one by one
for (i = 0; i < V; i++)
{
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++)
{
// If vertex k is on the shortest path from
// i to j, then update the value of dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// If distance of any vertex from itself
// becomes negative, then there is a negative
// weight cycle.
for (int i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
// driver program
int main()
{
/* Let us create the following weighted graph
1
(0)----------->(1)
/|\ |
| |
-1 | | -1
| \|/
(3)<-----------(2)
-1 */
int graph[V][V] = { {0 , 1 , INF , INF},
{INF , 0 , -1 , INF},
{INF , INF , 0 , -1},
{-1 , INF , INF , 0}};
if (negCyclefloydWarshall(graph))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// Java Program to check if there is a negative weight
// cycle using Floyd Warshall Algorithm
class GFG
{
// Number of vertices in the graph
static final int V = 4;
/* Define Infinite as a large enough value. This
value will be used for vertices not connected
to each other */
static final int INF = 99999;
// Returns true if graph has negative weight cycle
// else false.
static boolean negCyclefloydWarshall(int graph[][])
{
/* dist[][] will be the output matrix that will
finally have the shortest
distances between every pair of vertices */
int dist[][] = new int[V][V], i, j, k;
/* Initialize the solution matrix same as input
graph matrix. Or we can say the initial values
of shortest distances are based on shortest
paths considering no intermediate vertex. */
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
/* Add all vertices one by one to the set of
intermediate vertices.
---> Before start of a iteration, we have shortest
distances between all pairs of vertices such
that the shortest distances consider only the
vertices in set {0, 1, 2, .. k-1} as intermediate
vertices.
----> After the end of a iteration, vertex no. k is
added to the set of intermediate vertices and
the set becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++)
{
// Pick all vertices as source one by one
for (i = 0; i < V; i++)
{
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++)
{
// If vertex k is on the shortest path from
// i to j, then update the value of dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// If distance of any vertex from itself
// becomes negative, then there is a negative
// weight cycle.
for (i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
// Driver code
public static void main (String[] args)
{
/* Let us create the following weighted graph
1
(0)----------->(1)
/|\ |
| |
-1 | | -1
| \|/
(3)<-----------(2)
-1 */
int graph[][] = { {0, 1, INF, INF},
{INF, 0, -1, INF},
{INF, INF, 0, -1},
{-1, INF, INF, 0}};
if (negCyclefloydWarshall(graph))
System.out.print("Yes");
else
System.out.print("No");
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python Program to check
# if there is a
# negative weight
# cycle using Floyd
# Warshall Algorithm
# Number of vertices
# in the graph
V = 4
# Define Infinite as a
# large enough value. This
# value will be used
#for vertices not connected
# to each other
INF = 99999
# Returns true if graph has
# negative weight cycle
# else false.
def negCyclefloydWarshall(graph):
# dist[][] will be the
# output matrix that will
# finally have the shortest
# distances between every
# pair of vertices
dist=[[0 for i in range(V+1)]for j in range(V+1)]
# Initialize the solution
# matrix same as input
# graph matrix. Or we can
# say the initial values
# of shortest distances
# are based on shortest
# paths considering no
# intermediate vertex.
for i in range(V):
for j in range(V):
dist[i][j] = graph[i][j]
''' Add all vertices one
by one to the set of
intermediate vertices.
---> Before start of a iteration,
we have shortest
distances between all pairs
of vertices such
that the shortest distances
consider only the
vertices in set {0, 1, 2, .. k-1}
as intermediate vertices.
----> After the end of a iteration,
vertex no. k is
added to the set of
intermediate vertices and
the set becomes {0, 1, 2, .. k} '''
for k in range(V):
# Pick all vertices
# as source one by one
for i in range(V):
# Pick all vertices as
# destination for the
# above picked source
for j in range(V):
# If vertex k is on
# the shortest path from
# i to j, then update
# the value of dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j]):
dist[i][j] = dist[i][k] + dist[k][j]
# If distance of any
# vertex from itself
# becomes negative, then
# there is a negative
# weight cycle.
for i in range(V):
if (dist[i][i] < 0):
return True
return False
# Driver code
''' Let us create the
following weighted graph
1
(0)----------->(1)
/|\ |
| |
-1 | | -1
| \|/
(3)<-----------(2)
-1 '''
graph = [ [0, 1, INF, INF],
[INF, 0, -1, INF],
[INF, INF, 0, -1],
[-1, INF, INF, 0]]
if (negCyclefloydWarshall(graph)):
print("Yes")
else:
print("No")
# This code is contributed
# by Anant Agarwal.
C#
// C# Program to check if there
// is a negative weight cycle
// using Floyd Warshall Algorithm
using System;
namespace Cycle
{
public class GFG
{
// Number of vertices in the graph
static int V = 4;
/* Define Infinite as a large enough value. This
value will be used for vertices not connected
to each other */
static int INF = 99999;
// Returns true if graph has negative weight cycle
// else false.
static bool negCyclefloydWarshall(int [,]graph)
{
/* dist[][] will be the output matrix that will
finally have the shortest
distances between every pair of vertices */
int [,]dist = new int[V,V];
int i, j, k;
/* Initialize the solution matrix same as input
graph matrix. Or we can say the initial values
of shortest distances are based on shortest
paths considering no intermediate vertex. */
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i,j] = graph[i,j];
/* Add all vertices one by one to the set of
intermediate vertices.
---> Before start of a iteration, we have shortest
distances between all pairs of vertices such
that the shortest distances consider only the
vertices in set {0, 1, 2, .. k-1} as intermediate
vertices.
----> After the end of a iteration, vertex no. k is
added to the set of intermediate vertices and
the set becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++)
{
// Pick all vertices as source one by one
for (i = 0; i < V; i++)
{
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++)
{
// If vertex k is on the shortest path from
// i to j, then update the value of dist[i][j]
if (dist[i,k] + dist[k,j] < dist[i,j])
dist[i,j] = dist[i,k] + dist[k,j];
}
}
}
// If distance of any vertex from itself
// becomes negative, then there is a negative
// weight cycle.
for (i = 0; i < V; i++)
if (dist[i,i] < 0)
return true;
return false;
}
// Driver code
public static void Main()
{
/* Let us create the following weighted graph
1
(0)----------->(1)
/|\ |
| |
-1 | | -1
| \|/
(3)<-----------(2)
-1 */
int [,]graph = { {0, 1, INF, INF},
{INF, 0, -1, INF},
{INF, INF, 0, -1},
{-1, INF, INF, 0}};
if (negCyclefloydWarshall(graph))
Console.Write("Yes");
else
Console.Write("No");
}
}
}
// This code is contributed by Sam007.
Javascript
<script>
// JavaScript Program to check if there
// is a negative weight cycle
// using Floyd Warshall Algorithm
// Number of vertices in the graph
var V = 4;
/* Define Infinite as a large enough value. This
value will be used for vertices not connected
to each other */
var INF = 99999;
// Returns true if graph has negative weight cycle
// else false.
function negCyclefloydWarshall(graph)
{
/* dist[][] will be the output matrix that will
finally have the shortest
distances between every pair of vertices */
var dist = Array.from(Array(V), ()=>Array(V));
var i, j, k;
/* Initialize the solution matrix same as input
graph matrix. Or we can say the initial values
of shortest distances are based on shortest
paths considering no intermediate vertex. */
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
/* Add all vertices one by one to the set of
intermediate vertices.
---> Before start of a iteration, we have shortest
distances between all pairs of vertices such
that the shortest distances consider only the
vertices in set {0, 1, 2, .. k-1} as intermediate
vertices.
----> After the end of a iteration, vertex no. k is
added to the set of intermediate vertices and
the set becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++)
{
// Pick all vertices as source one by one
for (i = 0; i < V; i++)
{
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++)
{
// If vertex k is on the shortest path from
// i to j, then update the value of dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// If distance of any vertex from itself
// becomes negative, then there is a negative
// weight cycle.
for (i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
// Driver code
/* Let us create the following weighted graph
1
(0)----------->(1)
/|\ |
| |
-1 | | -1
| \|/
(3)<-----------(2)
-1 */
var graph = [ [0, 1, INF, INF],
[INF, 0, -1, INF],
[INF, INF, 0, -1],
[-1, INF, INF, 0]];
if (negCyclefloydWarshall(graph))
document.write("Yes");
else
document.write("No");
</script>
Yes
Este artículo es una contribución de Shivani Mittal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA