Nos dan un gráfico dirigido. Necesitamos calcular si el gráfico tiene un ciclo negativo o no. Un ciclo negativo es aquel en el que la suma total del ciclo se vuelve negativa.
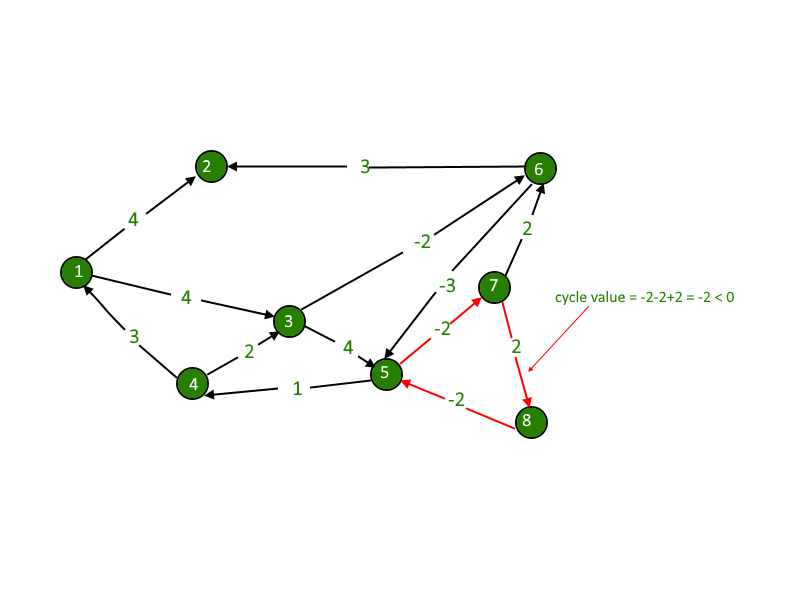
Los pesos negativos se encuentran en varias aplicaciones de gráficos. Por ejemplo, en lugar de pagar el costo de un camino, podemos obtener alguna ventaja si seguimos el camino.
Ejemplos:
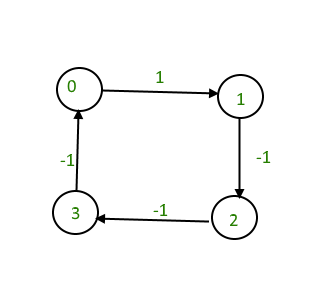
Input : 4 4
0 1 1
1 2 -1
2 3 -1
3 0 -1
Output : Yes
The graph contains a negative cycle.
Recomendado: Resuelva primero en «PRÁCTICA», antes de pasar a la solución.
La idea es utilizar el Algoritmo de Bellman-Ford .
A continuación se muestra un algoritmo para encontrar si hay un ciclo de peso negativo accesible desde la fuente dada.
- Inicialice las distancias desde la fuente a todos los vértices como infinito y la distancia a la fuente misma como 0. Cree una array dist[] de tamaño |V| con todos los valores infinitos excepto dist[src] donde src es el vértice de origen.
- Este paso calcula las distancias más cortas. Haz lo siguiente |V|-1 veces donde |V| es el número de vértices en el gráfico dado.
- Haga lo siguiente para cada borde uv.
- Si dist[v] > dist[u] + peso del borde uv, actualice dist[v].
- dist[v] = dist[u] + peso de la arista uv.
- Este paso informa si hay un ciclo de peso negativo en el gráfico. Haga lo siguiente para cada borde uv
- Si dist[v] > dist[u] + peso del borde uv, entonces el «Gráfico tiene un ciclo de peso negativo»
La idea del paso 3 es que el paso 2 garantiza las distancias más cortas si el gráfico no contiene un ciclo de peso negativo. Si iteramos a través de todos los bordes una vez más y obtenemos una ruta más corta para cualquier vértice, entonces hay un ciclo de peso negativo.
Implementación:
C++
// A C++ program to check if a graph contains negative
// weight cycle using Bellman-Ford algorithm. This program
// works only if all vertices are reachable from a source
// vertex 0.
#include <bits/stdc++.h>
using namespace std;
// a structure to represent a weighted edge in graph
struct Edge {
int src, dest, weight;
};
// a structure to represent a connected, directed and
// weighted graph
struct Graph {
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[graph->E];
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
bool isNegCycleBellmanFord(struct Graph* graph,
int src)
{
int V = graph->V;
int E = graph->E;
int dist[V];
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
return true;
}
return false;
}
// Driver program to test above functions
int main()
{
/* Let us create the graph given in above example */
int V = 5; // Number of vertices in graph
int E = 8; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1 (or A-B in above figure)
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
// add edge 1-4 (or A-E in above figure)
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
if (isNegCycleBellmanFord(graph, 0))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// Java program to check if a graph contains negative
// weight cycle using Bellman-Ford algorithm. This program
// works only if all vertices are reachable from a source
// vertex 0.
import java.util.*;
class GFG {
// a structure to represent a weighted edge in graph
static class Edge {
int src, dest, weight;
}
// a structure to represent a connected, directed and
// weighted graph
static class Graph {
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
Edge edge[];
}
// Creates a graph with V vertices and E edges
static Graph createGraph(int V, int E) {
Graph graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Edge[graph.E];
for (int i = 0; i < graph.E; i++) {
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
static boolean isNegCycleBellmanFord(Graph graph, int src) {
int V = graph.V;
int E = graph.E;
int[] dist = new int[V];
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for (int i = 0; i < V; i++)
dist[i] = Integer.MAX_VALUE;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for (int i = 0; i < E; i++) {
int u = graph.edge[i].src;
int v = graph.edge[i].dest;
int weight = graph.edge[i].weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])
return true;
}
return false;
}
// Driver Code
public static void main(String[] args) {
int V = 5, E = 8;
Graph graph = createGraph(V, E);
// add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleBellmanFord(graph, 0))
System.out.println("Yes");
else
System.out.println("No");
}
}
// This code is contributed by
// sanjeev2552
Python3
# A Python3 program to check if a graph contains negative
# weight cycle using Bellman-Ford algorithm. This program
# works only if all vertices are reachable from a source
# vertex 0.
# a structure to represent a weighted edge in graph
class Edge:
def __init__(self):
self.src = 0
self.dest = 0
self.weight = 0
# a structure to represent a connected, directed and
# weighted graph
class Graph:
def __init__(self):
# V. Number of vertices, E. Number of edges
self.V = 0
self.E = 0
# graph is represented as an array of edges.
self.edge = None
# Creates a graph with V vertices and E edges
def createGraph(V, E):
graph = Graph()
graph.V = V;
graph.E = E;
graph.edge =[Edge() for i in range(graph.E)]
return graph;
# The main function that finds shortest distances
# from src to all other vertices using Bellman-
# Ford algorithm. The function also detects
# negative weight cycle
def isNegCycleBellmanFord(graph, src):
V = graph.V;
E = graph.E;
dist = [1000000 for i in range(V)];
dist[src] = 0;
# Step 2: Relax all edges |V| - 1 times.
# A simple shortest path from src to any
# other vertex can have at-most |V| - 1
# edges
for i in range(1, V):
for j in range(E):
u = graph.edge[j].src;
v = graph.edge[j].dest;
weight = graph.edge[j].weight;
if (dist[u] != 1000000 and dist[u] + weight < dist[v]):
dist[v] = dist[u] + weight;
# Step 3: check for negative-weight cycles.
# The above step guarantees shortest distances
# if graph doesn't contain negative weight cycle.
# If we get a shorter path, then there
# is a cycle.
for i in range(E):
u = graph.edge[i].src;
v = graph.edge[i].dest;
weight = graph.edge[i].weight;
if (dist[u] != 1000000 and dist[u] + weight < dist[v]):
return True;
return False;
# Driver program to test above functions
if __name__=='__main__':
# Let us create the graph given in above example
V = 5; # Number of vertices in graph
E = 8; # Number of edges in graph
graph = createGraph(V, E);
# add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
# add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
# add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
# add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
# add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
# add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
# add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
# add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleBellmanFord(graph, 0)):
print("Yes")
else:
print("No")
# This code is contributed by pratham76
C#
// C# program to check if a graph contains negative
// weight cycle using Bellman-Ford algorithm. This program
// works only if all vertices are reachable from a source
// vertex 0.
using System;
using System.Collections;
using System.Collections.Generic;
class GFG {
// a structure to represent a weighted edge in graph
class Edge {
public int src, dest, weight;
}
// a structure to represent a connected, directed and
// weighted graph
class Graph {
// V-> Number of vertices, E-> Number of edges
public int V, E;
// graph is represented as an array of edges.
public Edge []edge;
}
// Creates a graph with V vertices and E edges
static Graph createGraph(int V, int E) {
Graph graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Edge[graph.E];
for (int i = 0; i < graph.E; i++) {
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
static bool isNegCycleBellmanFord(Graph graph, int src) {
int V = graph.V;
int E = graph.E;
int[] dist = new int[V];
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for (int i = 0; i < V; i++)
dist[i] = 1000000;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != 1000000 && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for (int i = 0; i < E; i++) {
int u = graph.edge[i].src;
int v = graph.edge[i].dest;
int weight = graph.edge[i].weight;
if (dist[u] != 1000000 && dist[u] + weight < dist[v])
return true;
}
return false;
}
// Driver Code
public static void Main(string[] args) {
int V = 5, E = 8;
Graph graph = createGraph(V, E);
// add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleBellmanFord(graph, 0))
Console.Write("Yes");
else
Console.Write("No");
}
}
// This code is contributed by rutvik_56
Javascript
<script>
// Javascript program to check if a graph contains negative
// weight cycle using Bellman-Ford algorithm. This program
// works only if all vertices are reachable from a source
// vertex 0.
// A structure to represent a weighted edge in graph
class Edge
{
constructor()
{
let src, dest, weight;
}
}
// A structure to represent a connected, directed and
// weighted graph
class Graph
{
constructor()
{
// V-> Number of vertices, E-> Number of edges
let V, E;
// graph is represented as an array of edges.
let edge = [];
}
}
// Creates a graph with V vertices and E edges
function createGraph(V,E)
{
let graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Array(graph.E);
for(let i = 0; i < graph.E; i++)
{
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
function isNegCycleBellmanFord(graph, src)
{
let V = graph.V;
let E = graph.E;
let dist = new Array(V);
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for(let i = 0; i < V; i++)
dist[i] = Number.MAX_VALUE;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for(let i = 1; i <= V - 1; i++)
{
for(let j = 0; j < E; j++)
{
let u = graph.edge[j].src;
let v = graph.edge[j].dest;
let weight = graph.edge[j].weight;
if (dist[u] != Number.MAX_VALUE && dist[u] +
weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for(let i = 0; i < E; i++)
{
let u = graph.edge[i].src;
let v = graph.edge[i].dest;
let weight = graph.edge[i].weight;
if (dist[u] != Number.MAX_VALUE &&
dist[u] + weight < dist[v])
return true;
}
return false;
}
// Driver Code
let V = 5, E = 8;
let graph = createGraph(V, E);
// Add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// Add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// Add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// Add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// Add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// Add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleBellmanFord(graph, 0))
document.write("Yes");
else
document.write("No");
// This code is contributed by unknown2108
</script>
No
¿Como funciona?
Como se discutió, el algoritmo de Bellman-Ford , para una fuente dada, primero calcula las distancias más cortas que tienen como máximo un borde en el camino. Luego, calcula los caminos más cortos con 2 aristas como máximo, y así sucesivamente. Después de la i-ésima iteración del bucle exterior, se calculan los caminos más cortos con como máximo i aristas. Puede haber un máximo |V| – 1 arista en cualquier camino simple, por eso el ciclo externo ejecuta |v| – 1 vez. Si hay un ciclo de peso negativo, entonces una iteración más daría una ruta corta.

¿Cómo manejar un gráfico desconectado (si el ciclo no es accesible desde la fuente)?
El algoritmo y el programa anteriores podrían no funcionar si el gráfico dado está desconectado. Funciona cuando todos los vértices son accesibles desde el vértice de origen 0.
Para manejar gráficos desconectados, podemos repetir el proceso para los vértices para los que la distancia es infinita.
Implementación:
C++
// A C++ program for Bellman-Ford's single source
// shortest path algorithm.
#include <bits/stdc++.h>
using namespace std;
// a structure to represent a weighted edge in graph
struct Edge {
int src, dest, weight;
};
// a structure to represent a connected, directed and
// weighted graph
struct Graph {
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[graph->E];
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
bool isNegCycleBellmanFord(struct Graph* graph,
int src, int dist[])
{
int V = graph->V;
int E = graph->E;
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
return true;
}
return false;
}
// Returns true if given graph has negative weight
// cycle.
bool isNegCycleDisconnected(struct Graph* graph)
{
int V = graph->V;
// To keep track of visited vertices to avoid
// recomputations.
bool visited[V];
memset(visited, 0, sizeof(visited));
// This array is filled by Bellman-Ford
int dist[V];
// Call Bellman-Ford for all those vertices
// that are not visited
for (int i = 0; i < V; i++) {
if (visited[i] == false) {
// If cycle found
if (isNegCycleBellmanFord(graph, i, dist))
return true;
// Mark all vertices that are visited
// in above call.
for (int i = 0; i < V; i++)
if (dist[i] != INT_MAX)
visited[i] = true;
}
}
return false;
}
// Driver program to test above functions
int main()
{
/* Let us create the graph given in above example */
int V = 5; // Number of vertices in graph
int E = 8; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1 (or A-B in above figure)
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
// add edge 1-4 (or A-E in above figure)
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
if (isNegCycleDisconnected(graph))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// A Java program for Bellman-Ford's single source
// shortest path algorithm.
import java.util.*;
class GFG{
// A structure to represent a weighted
// edge in graph
static class Edge
{
int src, dest, weight;
}
// A structure to represent a connected,
// directed and weighted graph
static class Graph
{
// V-> Number of vertices,
// E-> Number of edges
int V, E;
// Graph is represented as
// an array of edges.
Edge edge[];
}
// Creates a graph with V vertices and E edges
static Graph createGraph(int V, int E)
{
Graph graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Edge[graph.E];
for(int i = 0; i < graph.E; i++)
{
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
static boolean isNegCycleBellmanFord(Graph graph,
int src,
int dist[])
{
int V = graph.V;
int E = graph.E;
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for(int i = 0; i < V; i++)
dist[i] = Integer.MAX_VALUE;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for(int i = 1; i <= V - 1; i++)
{
for(int j = 0; j < E; j++)
{
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != Integer.MAX_VALUE &&
dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for(int i = 0; i < E; i++)
{
int u = graph.edge[i].src;
int v = graph.edge[i].dest;
int weight = graph.edge[i].weight;
if (dist[u] != Integer.MAX_VALUE &&
dist[u] + weight < dist[v])
return true;
}
return false;
}
// Returns true if given graph has negative weight
// cycle.
static boolean isNegCycleDisconnected(Graph graph)
{
int V = graph.V;
// To keep track of visited vertices
// to avoid recomputations.
boolean visited[] = new boolean[V];
Arrays.fill(visited, false);
// This array is filled by Bellman-Ford
int dist[] = new int[V];
// Call Bellman-Ford for all those vertices
// that are not visited
for(int i = 0; i < V; i++)
{
if (visited[i] == false)
{
// If cycle found
if (isNegCycleBellmanFord(graph, i, dist))
return true;
// Mark all vertices that are visited
// in above call.
for(int j = 0; j < V; j++)
if (dist[j] != Integer.MAX_VALUE)
visited[j] = true;
}
}
return false;
}
// Driver Code
public static void main(String[] args)
{
int V = 5, E = 8;
Graph graph = createGraph(V, E);
// Add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// Add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// Add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// Add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// Add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// Add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// Add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// Add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleDisconnected(graph))
System.out.println("Yes");
else
System.out.println("No");
}
}
// This code is contributed by adityapande88
Python3
# A Python3 program for Bellman-Ford's single source
# shortest path algorithm.
# The main function that finds shortest distances
# from src to all other vertices using Bellman-
# Ford algorithm. The function also detects
# negative weight cycle
def isNegCycleBellmanFord(src, dist):
global graph, V, E
# Step 1: Initialize distances from src
# to all other vertices as INFINITE
for i in range(V):
dist[i] = 10**18
dist[src] = 0
# Step 2: Relax all edges |V| - 1 times.
# A simple shortest path from src to any
# other vertex can have at-most |V| - 1
# edges
for i in range(1,V):
for j in range(E):
u = graph[j][0]
v = graph[j][1]
weight = graph[j][2]
if (dist[u] != 10**18 and dist[u] + weight < dist[v]):
dist[v] = dist[u] + weight
# Step 3: check for negative-weight cycles.
# The above step guarantees shortest distances
# if graph doesn't contain negative weight cycle.
# If we get a shorter path, then there
# is a cycle.
for i in range(E):
u = graph[i][0]
v = graph[i][1]
weight = graph[i][2]
if (dist[u] != 10**18 and dist[u] + weight < dist[v]):
return True
return False
# Returns true if given graph has negative weight
# cycle.
def isNegCycleDisconnected():
global V, E, graph
# To keep track of visited vertices to avoid
# recomputations.
visited = [0]*V
# memset(visited, 0, sizeof(visited))
# This array is filled by Bellman-Ford
dist = [0]*V
# Call Bellman-Ford for all those vertices
# that are not visited
for i in range(V):
if (visited[i] == 0):
# If cycle found
if (isNegCycleBellmanFord(i, dist)):
return True
# Mark all vertices that are visited
# in above call.
for i in range(V):
if (dist[i] != 10**18):
visited[i] = True
return False
# Driver code
if __name__ == '__main__':
# /* Let us create the graph given in above example */
V = 5 # Number of vertices in graph
E = 8 # Number of edges in graph
graph = [[0, 0, 0] for i in range(8)]
# add edge 0-1 (or A-B in above figure)
graph[0][0] = 0
graph[0][1] = 1
graph[0][2] = -1
# add edge 0-2 (or A-C in above figure)
graph[1][0] = 0
graph[1][1] = 2
graph[1][2] = 4
# add edge 1-2 (or B-C in above figure)
graph[2][0] = 1
graph[2][1] = 2
graph[2][2] = 3
# add edge 1-3 (or B-D in above figure)
graph[3][0] = 1
graph[3][1] = 3
graph[3][2] = 2
# add edge 1-4 (or A-E in above figure)
graph[4][0] = 1
graph[4][1] = 4
graph[4][2] = 2
# add edge 3-2 (or D-C in above figure)
graph[5][0] = 3
graph[5][1] = 2
graph[5][2] = 5
# add edge 3-1 (or D-B in above figure)
graph[6][0] = 3
graph[6][1] = 1
graph[6][2] = 1
# add edge 4-3 (or E-D in above figure)
graph[7][0] = 4
graph[7][1] = 3
graph[7][2] = -3
if (isNegCycleDisconnected()):
print("Yes")
else:
print("No")
# This code is contributed by mohit kumar 29
C#
// A C# program for Bellman-Ford's single source
// shortest path algorithm.
using System;
using System.Collections.Generic;
public class GFG
{
// A structure to represent a weighted
// edge in graph
public
class Edge
{
public
int src, dest, weight;
}
// A structure to represent a connected,
// directed and weighted graph
public
class Graph
{
// V-> Number of vertices,
// E-> Number of edges
public
int V, E;
// Graph is represented as
// an array of edges.
public
Edge []edge;
}
// Creates a graph with V vertices and E edges
static Graph createGraph(int V, int E)
{
Graph graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Edge[graph.E];
for(int i = 0; i < graph.E; i++)
{
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
static bool isNegCycleBellmanFord(Graph graph,
int src,
int []dist)
{
int V = graph.V;
int E = graph.E;
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for(int i = 0; i < V; i++)
dist[i] = int.MaxValue;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for(int i = 1; i <= V - 1; i++)
{
for(int j = 0; j < E; j++)
{
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != int.MaxValue &&
dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for(int i = 0; i < E; i++)
{
int u = graph.edge[i].src;
int v = graph.edge[i].dest;
int weight = graph.edge[i].weight;
if (dist[u] != int.MaxValue &&
dist[u] + weight < dist[v])
return true;
}
return false;
}
// Returns true if given graph has negative weight
// cycle.
static bool isNegCycleDisconnected(Graph graph)
{
int V = graph.V;
// To keep track of visited vertices
// to avoid recomputations.
bool []visited = new bool[V];
// This array is filled by Bellman-Ford
int []dist = new int[V];
// Call Bellman-Ford for all those vertices
// that are not visited
for(int i = 0; i < V; i++)
{
if (visited[i] == false)
{
// If cycle found
if (isNegCycleBellmanFord(graph, i, dist))
return true;
// Mark all vertices that are visited
// in above call.
for(int j = 0; j < V; j++)
if (dist[j] != int.MaxValue)
visited[j] = true;
}
}
return false;
}
// Driver Code
public static void Main(String[] args)
{
int V = 5, E = 8;
Graph graph = createGraph(V, E);
// Add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// Add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// Add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// Add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// Add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// Add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// Add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// Add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleDisconnected(graph))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
// This code is contributed by aashish1995
Javascript
<script>
// A Javascript program for Bellman-Ford's single source
// shortest path algorithm.
// A structure to represent a weighted
// edge in graph
class Edge
{
constructor()
{
let src, dest, weight;
}
}
// A structure to represent a connected,
// directed and weighted graph
class Graph
{
constructor()
{
// V-> Number of vertices,
// E-> Number of edges
let V, E;
// Graph is represented as
// an array of edges.
let edge=[];
}
}
// Creates a graph with V vertices and E edges
function createGraph(V,E)
{
let graph = new Graph();
graph.V = V;
graph.E = E;
graph.edge = new Array(graph.E);
for(let i = 0; i < graph.E; i++)
{
graph.edge[i] = new Edge();
}
return graph;
}
// The main function that finds shortest distances
// from src to all other vertices using Bellman-
// Ford algorithm. The function also detects
// negative weight cycle
function isNegCycleBellmanFord(graph,src,dist)
{
let V = graph.V;
let E = graph.E;
// Step 1: Initialize distances from src
// to all other vertices as INFINITE
for(let i = 0; i < V; i++)
dist[i] = Number.MAX_VALUE;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times.
// A simple shortest path from src to any
// other vertex can have at-most |V| - 1
// edges
for(let i = 1; i <= V - 1; i++)
{
for(let j = 0; j < E; j++)
{
let u = graph.edge[j].src;
let v = graph.edge[j].dest;
let weight = graph.edge[j].weight;
if (dist[u] != Number.MAX_VALUE &&
dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles.
// The above step guarantees shortest distances
// if graph doesn't contain negative weight cycle.
// If we get a shorter path, then there
// is a cycle.
for(let i = 0; i < E; i++)
{
let u = graph.edge[i].src;
let v = graph.edge[i].dest;
let weight = graph.edge[i].weight;
if (dist[u] != Number.MAX_VALUE &&
dist[u] + weight < dist[v])
return true;
}
return false;
}
// Returns true if given graph has negative weight
// cycle.
function isNegCycleDisconnected(graph)
{
let V = graph.V;
// To keep track of visited vertices
// to avoid recomputations.
let visited = new Array(V);
for(let i=0;i<V;i++)
{
visited[i]=false;
}
// This array is filled by Bellman-Ford
let dist = new Array(V);
// Call Bellman-Ford for all those vertices
// that are not visited
for(let i = 0; i < V; i++)
{
if (visited[i] == false)
{
// If cycle found
if (isNegCycleBellmanFord(graph, i, dist))
return true;
// Mark all vertices that are visited
// in above call.
for(let j = 0; j < V; j++)
if (dist[j] != Number.MAX_VALUE)
visited[j] = true;
}
}
return false;
}
// Driver Code
let V = 5, E = 8;
let graph = createGraph(V, E);
// Add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// Add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// Add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// Add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// Add edge 1-4 (or A-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// Add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// Add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// Add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
if (isNegCycleDisconnected(graph))
document.write("Yes");
else
document.write("No");
// This code is contributed by patel2127
</script>
No
Detección de ciclo negativo usando Floyd Warshall
Este artículo es una contribución de kartik . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA