Diferencia entre apertura y cierre en el procesamiento de imágenes digitales

La apertura y el cierre son operaciones duales que se utilizan en el procesamiento de imágenes digitales para restaurar una imagen erosionada. La apertura se utiliza generalmente para restaurar o recuperar la imagen original en la mayor medida posible. El cierre se usa generalmente para suavizar el contorno de la imagen distorsionada y fusionar las rupturas estrechas y los golfos largos y delgados. El cierre también se utiliza para eliminar los pequeños agujeros de la imagen obtenida.

La combinación de Apertura y Cierre generalmente se usa para limpiar artefactos en la imagen segmentada antes de usar la imagen para el análisis digital.

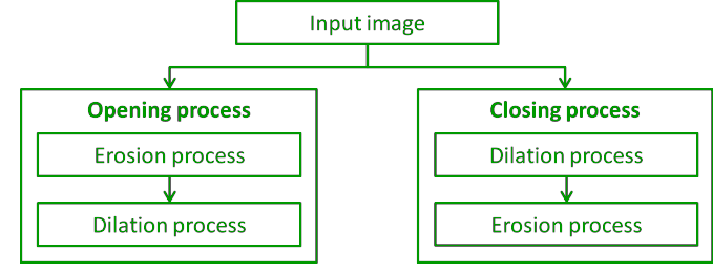
Algunas de las diferencias entre Apertura y Cierre son:

S. No.	Apertura	Clausura
1.	La apertura es un proceso en el que primero se realiza una operación de erosión y luego se realiza una operación de dilatación.	El cierre es un proceso en el que primero se realiza una operación de dilatación y luego una operación de erosión.
2.	La operación de apertura realizada en X e Y es la unión de todas las traslaciones de Y que encajan completamente dentro de X.	La operación de cierre realizada en X e Y es el complemento de la unión de todas las traslaciones de Y que no encajan completamente dentro de X.
3.	Elimina las finas protuberancias de la imagen obtenida.	Elimina los pequeños agujeros de la imagen obtenida.
4.	La operación de apertura realizada en X e Y está representada por (A o B).	La operación de cierre realizada en X e Y está representada por (A . B)
5.	La apertura se utiliza para eliminar el ruido interno de la imagen obtenida.	Closing se usa para alisar el contorno y fusionar roturas estrechas.

La apertura se denota por:

Properties of Opening are:
    1. XoY is a subset (subimage of X)
    2. If X is a subset of Z then XoY  is a subset of ZoY
    3.(XoY)oY = XoY

El cierre se denota por:

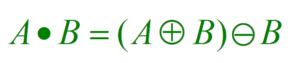
Properties of Closing are:
    1. X is a subset subimage of X.Y
    2. (X.Y).Y = X.Y