Diferencia entre Big Oh, Big Omega y Big Theta

Requisito previo: notaciones asintóticas , propiedades de las notaciones asintóticas , análisis de algoritmos
1. Notación oh grande (O): 

Se define como límite superior y el límite superior en un algoritmo es la mayor cantidad de tiempo requerido (el peor caso de rendimiento).
La notación oh grande se usa para describir el límite superior asintótico . 

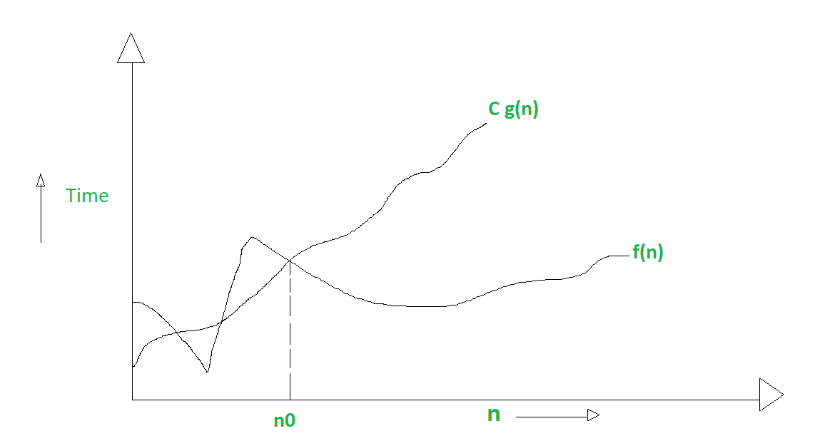
Matemáticamente, si f(n) describe el tiempo de ejecución de un algoritmo; f(n) es O(g(n)) si existen constantes positivas C y n0 tales que,

0 <= f(n) <= Cg(n) para todo n >= n0

n = se usa para dar un límite superior a una función. 
Si una función es O(n) , automáticamente también es O(n-cuadrado) . 

Ejemplo gráfico para Big oh (O) : 

2. Notación Big Omega (Ω): 

Se define como el límite inferior y el límite inferior en un algoritmo es la menor cantidad de tiempo requerida (la forma más eficiente posible, en otras palabras, el mejor de los casos).
Al igual que la notación O proporciona un límite superior asintótico , la notación Ω proporciona un límite inferior asintótico . 
 

Deje que f(n) defina el tiempo de ejecución de un algoritmo;
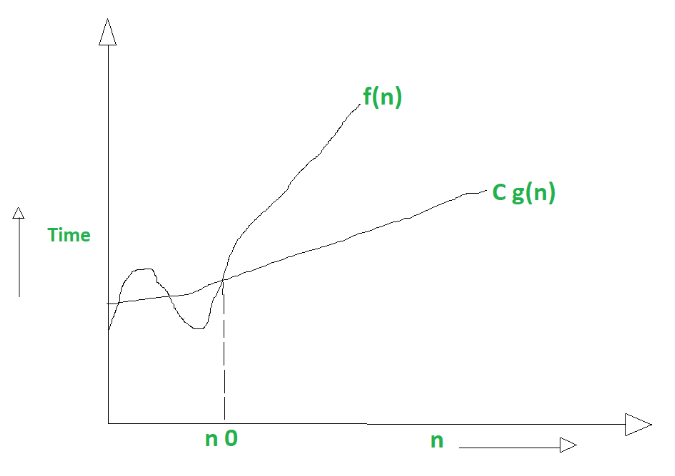
f(n) se dice que es Ω(g (n)) si existe una constante positiva C y (n0) tal que 

0 <= Cg(n) <= f(n) para todo n >= n0

n = se usa para dar un límite inferior a una función 
Si una función es Ω(n-cuadrada) automáticamente también es Ω(n) . 

Ejemplo gráfico para Big Omega (Ω): 

3. Notación Theta grande (Θ): 

Se define como el límite más estricto y el límite más estricto es el mejor de todos los peores tiempos que puede tomar el algoritmo.

Deje que f(n) defina el tiempo de ejecución de un algoritmo. 
f(n) se dice que es Θ(g(n)) si f(n) es O(g(n)) y f(n) es Ω(g(n)).

Matemáticamente, 

0 <= f(n) <= C1g(n) para n >= n0
0 <= C2g(n) <= f(n) para n >= n0

Combinando ambas ecuaciones, obtenemos:  

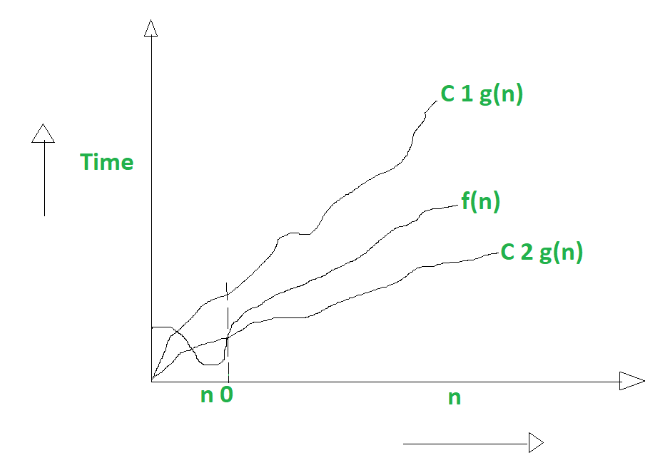
0 <= C2g(n) <= f(n) <= C1g(n) para n >= n0

La ecuación simplemente significa que existen constantes positivas C1 y C2 tales que f(n) está entre C2 g(n) y C1g(n). 
 
 Ejemplo gráfico de Big Theta (Θ) : 

Diferencia entre Big oh, Big Omega y Big Theta: 
 

S. No.	Gran Oh (O)	Omega grande ( Ω)	Gran Theta  (Θ)
1.	Es como (<=)  la tasa de crecimiento de un algoritmo es menor o igual a un valor específico.	Es como (>=)  la tasa de crecimiento es mayor o igual a un valor especificado.	Es como (==)  , lo que significa que la tasa de crecimiento es igual a un valor específico.
2.	El límite superior del algoritmo está representado por la notación Big O. Solo la función anterior está limitada por Big O. El enlace superior asintótico está dado por la notación Big O.	El límite inferior del algoritmo está representado por la notación Omega. El enlace inferior asintótico viene dado por la notación Omega.	El límite de la función desde arriba y desde abajo se representa mediante la notación theta. El comportamiento asintótico exacto se realiza mediante esta notación theta.
3.	Gran oh (O) – Límite superior	Big Omega (Ω) – Límite inferior	Big Theta (Θ) – Atado apretado
4.	Se define como límite superior y el límite superior en un algoritmo es la mayor cantidad de tiempo requerido (el peor caso de rendimiento).	Se define como el límite inferior y el límite inferior en un algoritmo es la menor cantidad de tiempo requerida (la forma más eficiente posible, en otras palabras, el mejor de los casos).	It is define as tightest bound and tightest bound is the best of all the worst case times that the algorithm can take.
5.	Mathematically: Big Oh is 0 <= f(n) <= Cg(n) for all n >= n0	Mathematically: Big Omega is 0 <= Cg(n) <= f(n) for all n >= n0	Mathematically – Big Theta is 0 <= C2g(n) <= f(n) <= C1g(n) for n >= n0

Para más detalles, consulte:
Diseño y Análisis de Algoritmos .