Diferencia entre convolución VS correlación

La correlación es una técnica matemática para ver qué tan cerca están relacionadas dos cosas. En términos de procesamiento de imágenes, se utiliza para calcular la respuesta de una máscara en una imagen. Se aplica una máscara sobre una array de izquierda a derecha. La máscara se desliza sobre la array de izquierda a derecha una unidad cada vez. Una vez que la máscara llega al extremo derecho, la máscara se desliza hacia abajo una unidad y nuevamente comienza de izquierda a derecha. La salida calculada se asigna al píxel central, mientras que los píxeles vecinos también se utilizan en el cálculo. La máscara o la array pueden ser 1-D o 2-D. Generalmente, la dimensión de la máscara se toma como un número impar, de modo que el píxel central se pueda encontrar fácilmente.

Ilustración:

Imagen, I = [100, 120, 100, 150, 160] Los índices de la imagen son 0, 1, 2, 3 y 4.

Máscara, H = [1/3, 1/3, 1/3] Los índices de la máscara son -1, 0 y 1.

Aplique la correlación entre la imagen y la máscara en el índice = 2 en la imagen.

J(2) = yo(1) . H(-1) + Yo(2) . H(0) + I(3) . Los índices H(1) se representan entre paréntesis.

J(2) = 120 x 1/3 + 100 x 1/3 + 150 x 1/3

J(2) = 370/3

En general, J = I. H

La correlación se denota por (.)

La fórmula de la correlación 1D: 

La fórmula de la correlación 2D: 

Nota:

• El tamaño de la imagen resultante depende del relleno.
• Si se permite el relleno, tamaño de la imagen resultante = tamaño de la imagen original (entrada)
• Si no se permite el relleno, el tamaño de la imagen resultante < tamaño de la imagen de entrada.

Una convolución es también una herramienta matemática que se usa para combinar dos cosas para producir el resultado. En el procesamiento de imágenes, la convolución es un proceso mediante el cual transformamos una imagen de entrada aplicando un kernel sobre ella en forma de píxeles. Cuando la máscara de convolución opera en un píxel en particular, realiza la acción considerando ese píxel y sus píxeles vecinos y el resultado se devuelve a ese píxel en particular. Por lo tanto, concluimos que la convolución en el procesamiento de imágenes es el operador de máscara. 

Cómo realizar la convolución

1. Voltee la máscara y haga la correlación.
2. La máscara 1D se voltea horizontalmente, ya que hay una sola fila.
3. La máscara 2D se voltea vertical y horizontalmente.
4. La máscara se desliza sobre la array de la imagen de izquierda a derecha.
5. Cuando la máscara se desplaza sobre la imagen, los elementos correspondientes de la máscara y la imagen se multiplican y se agregan los productos.
6. Este proceso se repite para todos los píxeles de la imagen.

Hay dos tipos de operadores en el procesamiento de imágenes. 

• Operador de punto:  mientras opera en un píxel en particular, solo toma un píxel como entrada que es él mismo. Por ejemplo, operación de aumento de brillo. Aumentamos la intensidad de cada píxel en el mismo valor para aumentar el brillo de la imagen.
• Operador de máscara:  al realizar una acción en un píxel en particular, toma el píxel en particular y sus píxeles vecinos como entrada. Operación de convolución.

Ilustración:

Imagen, I = [100, 120, 100, 150, 160]

Los índices de la imagen son 0, 1, 2, 3 y 4.

Máscara utilizada para la correlación, H = [1/3, 1/3, 1/3]

Los índices de la máscara son -1, 0 y 1.

Estamos usando la misma máscara, no la invertida, por lo tanto, usaremos los índices correctamente.

Aplicar convolución entre imagen y máscara en index=1 en la imagen.

J(2) = Yo(0) . H(1) + yo(1) . H(0) + I(2) . Los índices H(-1) se representan entre paréntesis.

J = I * H

La convolución se indica con (*).

El tamaño de la imagen resultante es el mismo que en el caso de la correlación.

La fórmula de convolución 1D:

La fórmula de la convolución 2D: 

Nota: La convolución y la correlación dan la misma respuesta si la máscara es simétrica. Tanto la correlación como la convolución tienen una naturaleza similar. Pero usamos la convolución ampliamente en el procesamiento de imágenes debido a sus siguientes propiedades.

Propiedades de la convolución

• La convolución es de naturaleza asociativa, pero no la correlación. es decir 
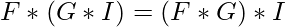
• La convolución es de naturaleza conmutativa. es decir 
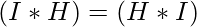
• La convolución sigue a la linealidad. es decir, 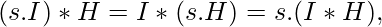  donde s es cualquier constante y se multiplica por la máscara o la imagen.
• La convolución sigue a la separabilidad si la máscara es separable. es decir, si

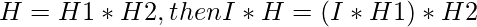
 Ventaja de la separabilidad

Si el kernel es separable, puede ahorrar costos computacionales.

Paso 1: la inicialización de la array se realiza en una línea en Matlab, 
el orden de la array no importa.

K = [1, 2, 3; 2, 4, 5];

Paso 2: el método incorporado de MatLab se usa para crear una array de unos:

 H = ones(3,3).*1/9;

Paso 3: Hemos usado (.) antes de *, porque (.) significa que estamos multiplicando todos los elementos de la array (3, 3) por 1/9.

Inicializar la máscara lineal de orden 1 por 3:

 H1=ones(1,3).*1/3;

Inicialice la máscara de transposición, que está separada de la máscara principal:

H2=H1'

Paso 4: la convolución entre la array K y la máscara H se aplica utilizando la función incorporada de Matlab «conv2»

KH = conv2(K, H, 'same');

Paso 5: Convolución entre la array K y la máscara H1: 

KH1 = conv2(K, H1, 'same');

Paso 6: Convolución entre la array de resultados KH1 y la máscara H2: 

KH2 = conv2(KH1, H2, 'same');

Ejemplo:

% MATLAB Code for separable mask
% D convolution
% Define the matrix.
 K=[9 18 9 27 36; 
    81 9 45 54 9;
    36 18 63 72 9];
  
% Define the averaging mask.
  H = ones(3,3).*1/9;
  
% Separate the mask.
 H1 = ones(1,3).*1/3;
  
% Transpose of separated mask.
 H2 = H1';
  
% Perform the same convolution.
  KH = conv2(K,H,'same')
  KH1 = conv2(K,H1,'same')
  KH2 = conv2(KH1,H2,'same')

Producción: 

Explicación del código: 

• Primero, definimos la imagen de la array.
• Después de la creación de la array, definimos la máscara de promedio principal, denominada H.
• Se definen máscaras separables H1 y H2.
• La segunda máscara es la transposición de mask1.
• La convolución entre la array K y la máscara H se calcula en la variable KH.
• La convolución entre la array K y la máscara H1 se almacena en la variable KH1.
• KH2 = conv2(KH1, H2, ‘igual’); Esta línea aplica la convolución entre la array de resultados KH1 y las máscaras H2.
  Este resultado es el mismo que KH.