Montón binario :
un montón binario es un árbol binario con las siguientes propiedades.
- Es un árbol binario completo , es decir, todos los niveles están completamente llenos, excepto posiblemente el último nivel y el último nivel tiene todas las claves como sea posible. Esta propiedad de Binary Heap los hace aptos para almacenarse en una array.
- Un montón binario es un montón mínimo o un montón máximo . En un montón binario mínimo, la clave en la raíz debe ser mínima entre todas las claves presentes en el montón binario. La misma propiedad debe ser recursivamente verdadera para todos los Nodes en Binary Tree . Max Binary Heap es similar a Min Heap .
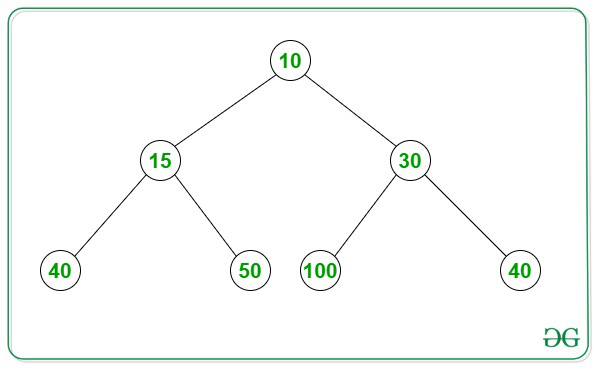
Ejemplo de Min-Heap:
Montón binomial:
un montón binomial es una colección de árbol binomial donde cada árbol binomial sigue la propiedad Min-Heap y puede haber como máximo un árbol binomial de cualquier grado.
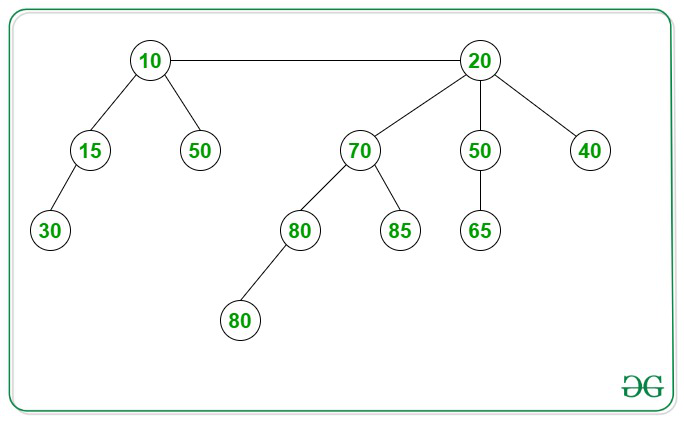
Ejemplo de montón binomial:
La diferencia clave entre un montón binario y un montón binomial es cómo se estructuran los montones. En un montón binario, el montón es un solo árbol, que es un árbol binario completo. En un montón binomial, el montón es una colección de árboles más pequeños (es decir, un bosque de árboles), cada uno de los cuales es un árbol binomial. Se puede construir un árbol binario completo para contener cualquier número de elementos, pero el número de elementos en un árbol binomial de algún orden N es siempre 2*N . En consecuencia, se necesita un árbol binario completo para respaldar un montón binario, pero es posible que necesitemos varios árboles binomiales para respaldar un montón binomial.
Fibonacci Heap :
Al igual que Binomial Heap,Fibonacci Heapes una colección de árboles con propiedad Min-Heap o Max-Heap. En Fibonacci Heap, los árboles pueden tener cualquier forma, incluso todos los árboles pueden ser Nodes únicos (esto es diferente a Binomial Heap donde cada árbol tiene que ser un árbol binomial). Fibonacci Heap mantiene un puntero a un valor mínimo (que es la raíz de un árbol). Todas las raíces de los árboles están conectadas mediante unalista circular doblemente enlazada, por lo que se puede acceder a todas ellas con un solo puntero ‘min’.
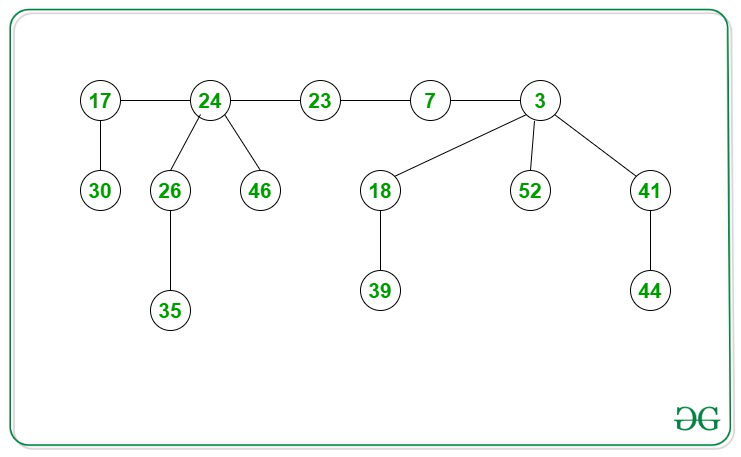
Ejemplo de montón de Fibonacci:
La diferencia en las complejidades temporales de varias operaciones asociadas con el montón binario, el montón binomial y los montones de Fibonacci se mencionan en la siguiente tabla.
| Operación | montón binario | Montón binomial | Montón de Fibonacci |
|---|---|---|---|
| insertar | O (registro N) | O (registro N) | O(1) |
| encontrar-min | O(1) | O (registro N) | O(1) |
| Eliminar | O (registro N) | O (registro N) | O (registro N) |
| disminuir-clave | O (registro N) | O (registro N) | O(1) |
| Unión | EN) | O (registro N) | O(1) |
Publicación traducida automáticamente
Artículo escrito por prashant_srivastava y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA